栈---定义、应用（递归、后缀表达式实现数学表达式求值）

一、定义

栈是限定仅在表尾进行插入和删除操作的线性表。因此，栈的表尾端称为栈顶；表头端称为栈底。不含任何数据元素的栈称为空栈。栈又称为后进先出(Last In First Out)的线性表，简称LIF0结构。

理解栈的定义需要注意：首先它是一个线性表，也即栈元素具有线性关系，即前驱后继关系。只不过它是一种特殊的线性表而已。

栈的插入操作，叫作进栈，也称压栈、入栈。栈的删除操作，叫作出找，也有的叫作弹栈。

如线性表一样，栈也有顺序存储与链式存储。

二、应用

1、用浏览器上网时，不管什么浏览器都有一个“后退”键，你点击后可以按访问顺序的逆序加载浏览过的网页。即使你从一个网页开始，连续点了几十个链接跳转，你点“后退” 时，还是可以像历史倒退一样，回到之前浏览过的某个页面。

2、很多类似的软件，比如Word、Photoshop等文档或图像编辑软件中，都有撤销(undo)的操作，也是用栈这种方式来实现的，当然不同的软件具体实现代码会有很大差异，不过原理其实都是一样的。

3、实现递归—斐波那契数列

斐波那契数列迭代版本：

#include "stdio.h"

int main()
{
    int i;
    int a[20];
    printf("迭代显示斐波那契数列：\n");
    a[0]=0;
    a[1]=1;
    printf("%d ",a[0]);
    printf("%d ",a[1]);
    for(i = 2;i < 20;i++)
    {
        a[i] = a[i-1] + a[i-2];
        printf("%d ",a[i]);
    }
    printf("\n");
    return 0;
}

斐波那契数列递归版本：

#include "stdio.h"

int Fbi(int i)  // 斐波那契的递归函数 
{
    if( i < 2 )
        return i == 0 ? 0 : 1;
    return Fbi(i - 1) + Fbi(i - 2);  
}

int main()
{
    int i;

    printf("递归显示斐波那契数列：\n");
    for(i = 0;i < 20;i++)
        printf("%d ", Fbi(i));
    return 0;
}

对比两种实现斐波那契的代码。迭代和递归的区别是：迭代使用的是循环结构，递归使用的是选择结构。

递归能使程序的结构更清晰、更简洁、更容易让人理解，从而减少读懂代码的时间。但是大量的递归调用会建立函数的副本，会耗费大量的时间和内存。
迭代则不需要反复调用函数和占用额外的内存。因此我们应该视不同 情况选择不同的代码实现方式。

递归和栈有什么关系呢？

前面我们已经看到递归是如何执行它的前行和退回阶段的。递归过程退回的顺序是它前行顺序的
逆序。在退回过程中，可能要执行某些动作，包括恢复在前行过程中存储起来的某些数据。

这种存储某些数据，并在后面又以存储的逆序恢复这些数据，以提供之后使用的需求，显然很符合栈这样的数据结构，因此，编译器使用栈实现递归就没什么好惊讶的了。

简单的说，就是在前行阶段，对于每一层递归，函数的局部变量、参数值以及返回地址都被压入栈中。在退回阶段，位于栈顶的局部变量、参数值和返回地址被弹出，用于返回调用层次中执行代码的其余部分，也就是恢复了调用的状态。！！！！！

4、数学表达式的求值—后缀表达式

对于9+(3-1)×3+10/2而言，如何用计算机实现求值？

仔细观察后发现，括号都是成对出现的，有左括号就一定会有右括号，对于多重括号，最终也是完全嵌套匹配的。这用栈结构正好合适，只有碰到左括号，就将此左括号进找，不管表达式有多少重括号，反正遇到左括号就进栈，而后面出现右括号时，就让栈顶的左括号出栈，期间让数字运算，这样，最终有括号的表达式从左到右巡査一遍，栈应该是由空到有元素，最终再因全部匹配成功后成为空栈的结果。

但对于四则运算，括号也只是当中的一部分，先乘除后加减使得问题依然复杂， 如何有效地处理它们呢？波兰逻辑学家Jan tukasiewicz想到了一种不需要括号的后缀表达法，我们也把它称为逆波兰（Reverse Polish Notation, RPN)表示。

对于9+(3-1)*3+10/2如果要用后缀表示法应该是什么样子：

9 3 1-3*+ 10 2/+

这样的表达式称为后缀表达式，叫后缀的原因在于所有的符号都是在要运算数字的后面出现。

规则：

从左到右遍历表达式的每个数字和符号，遇到是数字就进栈，遇到是符号，就将处于栈顶两个数
字出栈，进行运算，运算结果进栈，一直到最终获得结果。

步骤：
（1）初始化一个空栈。此桟用来对要运算的数字进出使用。
（2）后缀表达式中前三个都是数字，所以9、3、1进栈。

（3）接下来是减号“-”，所以将栈中的1出栈作为减数，3出栈作为被减数，并运算3-1得到2，再将2进栈。
（4）接着是数字3进栈。

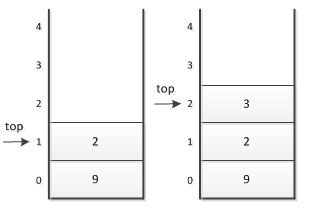
（5）后面是乘法“*”，也就意味着栈中3和2出栈，2与3相乘，得到6，并将6进栈。
（6） 下面是加法“+”，所以找中6和9出找，9与6相加，得到15，将15进栈。

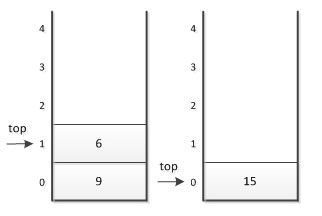
（7）接着是10与2两数字进栈。
（8）接下来是除号“/”因此，栈顶的2与10出栈，10与2相除，得到5，将5进栈。

（9）最后一个是符号“+”，所以15与5出栈并相加，得到20，将20进栈。
（10）结果是20出栈，栈变为空。

综上，我们实现了利用后缀表达式对数学表达式求值。

这个后缀表达式9 3 1-3*+ 10 2/+是如何通过算式9+(3-1)*3+10/2变化而来的呢？

我们把平时所用的标准四则运算表达式，即9+(3-1)*3+10/2叫做中缀表达式。因为所有的运算符号都在两数字的中间，现在我们的问题就是中缀到后缀的转化。

中缀表达式9+(3-1)*3+10/2转化为后缀表达式9 3 1-3*+ 10 2/+的规则：

从左到右遍历中缀表达式的每个数字和符号，若是数字就输出，即成为后缀表达式的一部分；若
是符号，则判断其与栈顶符号的优先级，是右括号或优先级低于栈顶符号（乘除优先加减）则栈
顶元素依次出栈并输出，并将当前符号进栈，一直到最终输出后缀表达式为止。

具体过程：

（1）初始化一空栈，用来对符号进出栈使用。
（2）第一个字符是数字9，输出9，后面是符号“+”，进栈。

（3）第三个字符是“(”,依然是符号，因其只是左括号，还未配对，故进栈。
（4）第四个字符是数字3，输出，总表达式为9 3,接着是“-”进栈。

（5）接下来是数字1，输出，总表达式为9 3 1，后面是符号“)”，此时，我们需要去匹配此前的“(”，所以栈顶依次出栈，并输出，直到“(”出栈为止。此时左括号上方只有“-”，因此输出“-”，总的输出表达式为9 3 1 -
（6）接着是数字3，输出，总的表达式为9 3 1 - 3 。紧接着是符号“*”，因为此时的栈顶符号为“+”号，优先级低于“* ”，因此不输出，进栈。

（7）之后是符号“+”，此时当前栈顶元素比这个“+”的优先级高，因此栈中元素出栈并输出（没有比“+”号更低的优先级，所以全部出栈），总输出表达式为 9 3 1 - 3 * +.然后将当前这个符号“+”进栈。也就是说，前6张图的栈底的“+”是指中缀表达式中开头的9后面那个“+”，而下图中的栈底（也是栈顶）的“+”是指“9+(3-1)*3+”中的最后一个“+”。

（8）紧接着数字10，输出，总表达式变为9 3 1-3 * + 10。

（9）最后一个数字2,输出，总的表达式为 9 3 1-3*+ 10 2
（10）因已经到最后，所以将栈中符号全部出栈并输出。最终输出的后缀表达式结果为 9 3 1-3*+ 10 2/+

从刚才的推导中你会发现，要想让计算机具有处理我们通常的标准（中缀）表达式的能力，最重要的就是两步：

（1）将中缀表达式转化为后缀表达式（栈用来进出运算的符号）。
（2）将后缀表达式进行运算得出结果（栈用来进出运算的数字）。

整个过程都充分利用了栈的后进先出特性来处理。