Oppo笔试题练习

序列1234567891011121314

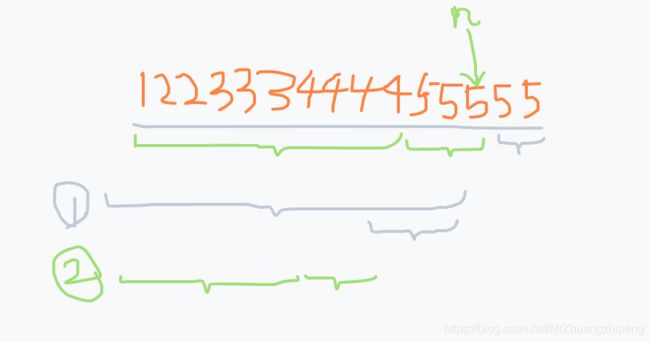
序列122333444455555

序列123344455555 

 

(1)，(2，2)，(3，3，3)，(4，4，4，4)，……
规律：第n组有n个数，值均为n
前n组共1+2+...+n=n(n+1)/2个数
令n(n+1)/2≤200
n(n+1)≤400
n为正整数，n≤19
200-19×20/2=10
19+1=20
第200个数是第20组的第10个数，是20

链接：https://www.nowcoder.com/questionTerminal/2e4363c23c6741f98319d5a7e3882325
来源：牛客网
 

在vivo产线上，每位职工随着对手机加工流程认识的熟悉和经验的增加，日产量也会不断攀升。

假设第一天量产1台，接下来2天(即第二、三天)每天量产2件，接下来3天(即第四、五、六天)每天量产3件 ... ... 

以此类推，请编程计算出第n天总共可以量产的手机数量。

 

class Solution {
public:
    /**
     *
     * @param n int整型 第n天
     * @return int整型
     */
    int solution(int n) {
        // write code here

        //122333444455555
        //求出第n天位于哪个组内
        int SumDay = 0;
        int i = 0;
        for (i = 0; SumDay < n; i++) {
            SumDay += i;//最后SumDay会超出n,所以最终结果需要减去 i * (SumDay - n);
        }
        i--;//因为i多加了一次了，非常重要，没理解好for循环
        int Res = 0;
        for (int j = 1; j <= i; j++) {
            Res += j * j;
        }
        Res = Res - (SumDay - n) * i;
        return Res;
    }
};

链接：https://www.nowcoder.com/questionTerminal/2e4363c23c6741f98319d5a7e3882325
来源：牛客网

class Solution {
public:
    /**
     *
     * @param n int整型 第n天
     * @return int整型
     */
    int solution(int n) {
        // write code here
        int sum, mount, i;
        mount = sum = 0;
        for(i = 1; sum + i < n; ++i){
            mount += i * i;
            sum += i;
        }
        mount += i * (n - sum);
        return mount;
    }

 

 

链接：https://www.nowcoder.com/questionTerminal/c552248efdbd41a18d35b7a2329f7ad8?answerType=1&f=discussion
来源：牛客网
 

现有一个 3x3 规格的 Android 智能手机锁屏程序和两个正整数 m 和 n ，请计算出使用最少m 个键和最多 n个键可以解锁该屏幕的所有有效模式总数。

其中有效模式是指：

1、每个模式必须连接至少m个键和最多n个键；

2、所有的键都必须是不同的；

3、如果在模式中连接两个连续键的行通过任何其他键，则其他键必须在模式中选择，不允许跳过非选择键（如图）；

4、顺序相关，单键有效（这里可能跟部分手机不同）。

 

输入：m,n

代表允许解锁的最少m个键和最多n个键
输出：

满足m和n个键数的所有有效模式的总数

 

分析：这题是真的恶心，需要考虑到下面这种情况，代码也就是

 

bool visited[10];
static int conn[8][3] = {
    {0, 2, 1}, {3, 5, 4}, {6, 8, 7}, {0, 6, 3}, {1, 7, 4},
                             {2, 8, 5}, {0, 8, 4}, {2, 6, 4}};//为了isValidPath
class Solution {

public:
    /**
     * 实现方案
     * @param m int整型 最少m个键
     * @param n int整型 最多n个键
     * @return int整型
     */

    bool isValidPath(int to , int from){
        if(to < from) swap(to,from); //因为本身conne中定义的i>j
        for(int i = 0 ; i < 8; i++){
            if(from == conn[i][0] && to == conn[i][1]){
                if (visited[conn[i][2]]) return true;
                return false;
            }
        }
        return true;//如果两个点本身就是相邻的，那么直接返回
    }
    
    int dfs(int start,int RequestLen,int CurLen){
        int count = 0 ;
        visited[start] = true;
        if(CurLen == RequestLen){
            count++;
        }else{     
           for(int i = 0 ; i < 9; i++){
            if(visited[i] == true || i == start) continue;
            if(isValidPath(i,start)){
                count += dfs(i,RequestLen,CurLen+1);
            }
        }
            
   }   
       
        visited[start] = false;
        return count;
    }
    
    int Count(int Request){
        int count = 0;
        int tmp = dfs(1,Request,1);//从1开始，然后要求长度为Request，当前长度为1
        count += 4*tmp;
        
        
        tmp = dfs(2,Request,1);
        count += 4*tmp;
        
        
        tmp = dfs(4,Request,1);
        count += tmp;
        
        
        return count;
    }
    
    int solution(int m, int n) {
        // write code here
        int Res = 0;//必须初始化为0
        for(int i =  m ;  i <= n ; i++){
            Res += Count(i);
        }
        return Res;
    }
};

另外一位大佬写得，真的佩服

class Solution {
public:
    /**
     * 实现方案
     * @param m int整型 最少m个键
     * @param n int整型 最多n个键
     * @return int整型
     */
    int total = 0, M, N;
    bool used[10];
    int id[10][2] = {
    {0, 0}, {1, 1}, {1, 2}, {1, 3},
                     {2, 1}, {2, 2}, {2, 3},
                     {3, 1}, {3, 2}, {3, 3}};
    int gcd(int a, int b) {
        return !b ? a : gcd(b, a % b);
    }
    int ID(int x, int y) {
        return (x - 1) * 3 + y;
    }
    bool check(int x, int y) {
        int tx = id[x][0], ty = id[x][1];
        int sx = id[y][0], sy = id[y][1];
        int t = gcd(abs(tx - sx), abs(ty - sy));
        if (t == 1) return true;//如果相邻，就返回true
        return used[ID((tx + sx) / 2, (ty + sy) / 2)];//如果不是相邻，但是中间节点是访问过了的化
    }
    void dfs(int x, int k) {
        if (k >= M && k <= N)
            total ++;
        if (k >= N)
            return;
        used[x] = 1;
        for (int i = 1; i <= 9; i++)
            if (!used[i] && check(x, i))//如果没访问过，并且可以构成一条路径的话
                dfs(i, k + 1);
        used[x] = 0;
    }
    int solution(int m, int n) {
        M = m, N = n;
        for (int i = 1; i <= 9; i++)
            dfs(i, 1);
        return total;
        // write code here
    }
};

 

 

现给定任意正整数 n，请寻找并输出最小的正整数 m（m>9），使得 m 的各位（个位、十位、百位 ... ...）之乘积等于n，若不存在则输出 -1。

输入：36

输出：49

思路：每一次尽可能地先将位数大的进行输出,感谢牛客网网友们。

使用递归的思路

class Solution {
public:
    /**
     * 输入一个整形数值，返回一个整形值
     * @param n int整型 n>9
     * @return int整型
     */
    int solution(int n) {
        // write code here
        int res =  helper(n);
        if(res > 0) return res;
        return -1;
    }
    int helper(int n ){
        if(n <= 9){
            return n;
        } 
        for(int i = 9 ; i > 1; i--){
            if(n%i ==0){
               return helper(n/i) * 10 + i;
            }
        }
        return -1;//比如11
    }
};

 

class Solution {
public:
    /**
     * 输入一个整形数值，返回一个整形值
     * @param n int整型 n>9
     * @return int整型
     */
    int solution(int n) {
        // write code here
        int res = 0;
        int curBit = 1;
        for(int i = 9 ; i > 1; i--){
            while(n%i == 0){
                n = n/i;
                res = i * curBit + res;
                curBit = curBit * 10;
            }
        }
        return n == 1 ? res : -1;
    }

};