matplotlib极坐标与雷达图

极坐标系

在画雷达图前，得先了解一下极坐标系。

之前绘制的折线图、柱形图等几乎都是在直角坐标系下绘制的，但雷达图是在极坐标上绘制的，所以首先要在画布（figure）上绘制极坐标系，很简单，像这样：

plt.figure() #创建一张画布
plt.subplot(111,polar=True) #在画布上绘制极坐标系

这样就绘制好极坐标系（polar表示极坐标）了，以前我们都没有添加polar参数，所以默认绘制的是直角坐标系。

接下来我们还是使用plt.plot(x,y) 这个本来是绘制折线图的函数来绘制，可以理解为在极坐标上画的折线图（这样的折线图是闭合的）;

还有就是这个参数要重新理解一下，x，y在直角坐标系充当了自变量和因变量的角色，而在极坐标系中扮演这两个角色的分别是角度angle（或theta，即$\theta$），以及极径 r,所以就变成了这样：plt.plot(angle, r) 。

其他参数如颜色（color或c）设置、线宽（linewidth或lw）、图例（label）等都不变。

接下来就用 plt.plot() 在极坐标系上绘制一个圆。

回忆圆的极坐标公式：（圆心在极点）
$$\{\begin{array}{l}r=R\\ 0\le \theta <2\pi \end{array}$$

import matplotlib.pyplot as plt
import numpy as np

angle = np.linspace(0, 2*np.pi, 50) #角度范围0~2π
R = 1
r = R * np.ones(50) #产生50个1，再与半径R相乘

plt.figure()
plt.subplot(111, polar=True)
plt.plot(angle, r, c='r')

plt.ylim(0, 2)
plt.yticks([0, 0.5, 1.0, 1.5, 2.0])

plt.show()

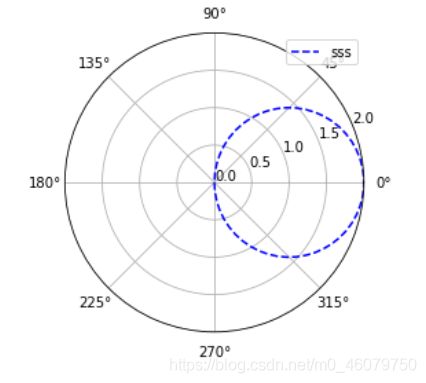
圆心不在极点的圆：
$$\{\begin{array}{l}r=2R\times cos\theta \\ -\frac{\pi }{2}\le \theta <\frac{\pi }{2}\end{array}$$

import matplotlib.pyplot as plt
import numpy as np

angle = np.linspace(-0.5 * np.pi, 0.5 * np.pi, 50) #角度范围
R = 1
r = 2 * R * np.cos(angle)  #这是因变量r关于自变量的关系式

plt.figure()
plt.subplot(111, polar=True)
plt.plot(angle, r, ls='--', c='blue',label='sss') 
plt.legend(loc='best')

plt.ylim(0, 2)
plt.yticks([0, 0.5, 1.0, 1.5, 2.0])

plt.show()

要注意 r 的数据个数要与 angle 相同。

好了，极坐标先讲这么多，接下来讲雷达图。

雷达图

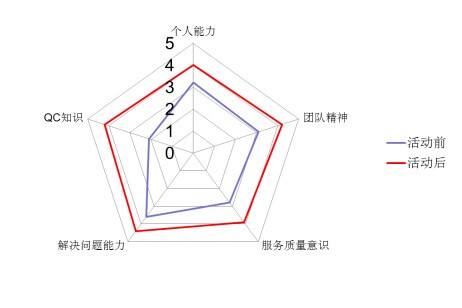
百度搜一张雷达图看看：

看了这个图，我们假想，如果在极坐标图上一点一点地绘制几个点，不就能绘制一张雷达图了吗? 好，说干就干，代码撸起来：

给出一组数据：values = [4, 3, 2, 6, 5]

（在撸之前，要注意一点，就是最后画完后还要回到起点，因此绘图使用的values应该是 [4,3,2,6,5,4] 最后一个数要与第一个数一样；同理，角度的最后一个值也要和第一个一样。为了方便，我们用 函数：

np.append(values, [values[0]])

来把第0个值添加到values的末尾，最后函数返回这个新的values）

#先绘制极坐标系 
plt.figure()
plt.subplot(111,polar=True)

#准备绘图数据
values = [4,3,2,6,5]
angles = np.linspace(0, 2*np.pi, len(values),endpoint=False) #产生与values个数一样的角度
#endpoint表示最后得到的数据最后一个数是否是 2*np.pi，我们不要这个值

values = np.append(values, [values[0]]) #将第0个数据添加到末尾
angles = np.append(angles, [angles[0]]) #将第0个数据添加到末尾

#开始绘图
plt.plot(angles, values)

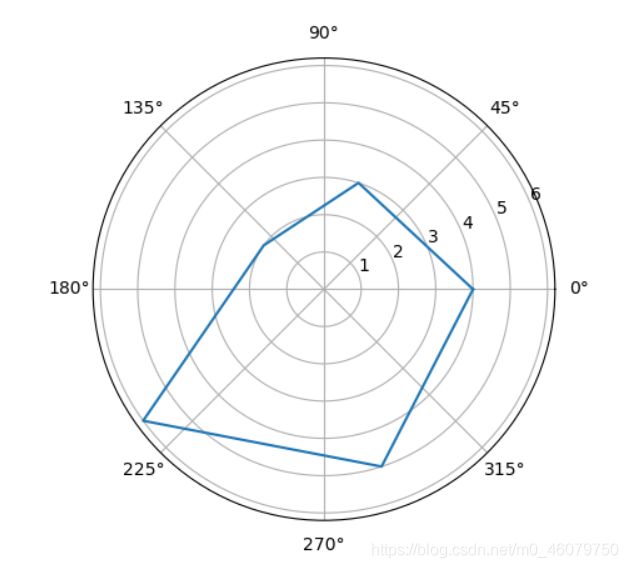
plt.show()

看下效果：

可以再修饰一下，在plt.show()之前添加下面的语句：

plt.style.use('seaborn') #使用seaborn绘图风格的背景，也可以用ggplot绘图风格，
	#注意，这句代码必须放在创建画布之前，甚至如果有中文字体出现也要放在字体设置之前

names = ['aa','bb','cc','dd','ee']
plt.xticks(angles, names, fontsize=15)
plt.yticks(range(0,7,2),fontsize=13)

plt.plot(angles, values, marker='o')  #设置标签

plt.fill(angles, values, color='b',alpha=0.15) #设置填充

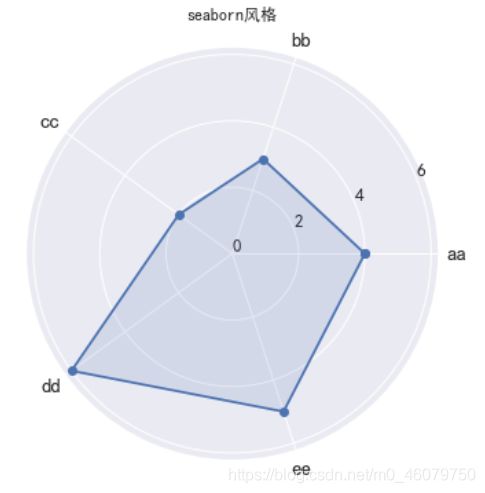
完整代码：

import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt

plt.style.use('seaborn') #使用绘图风格，注意代码位置

mpl.rcParams['font.family']='SimHei'         #中文字体
mpl.rcParams['font.sans-serif'] = 'SimHei'

#先绘制极坐标系 
plt.figure()
plt.subplot(111,polar=True)

#准备绘图数据
values = [4,3,2,6,5]
angles = np.linspace(0, 2*np.pi, len(values),endpoint=False) #产生与values个数一样的角度
#endpoint表示最后得到的数据最后一个数是否是 2*np.pi，我们不要这个值

values = np.append(values, [values[0]]) #将第0个数据添加到末尾
angles = np.append(angles, [angles[0]]) #将第0个数据添加到末尾
names = ['aa','bb','cc','dd','ee']
#开始绘图
plt.plot(angles, values, marker='o')
plt.fill(angles, values,alpha=0.15) #设置填充

plt.xticks(angles, names, fontsize=15)
plt.yticks(range(0,7,2),fontsize=13)

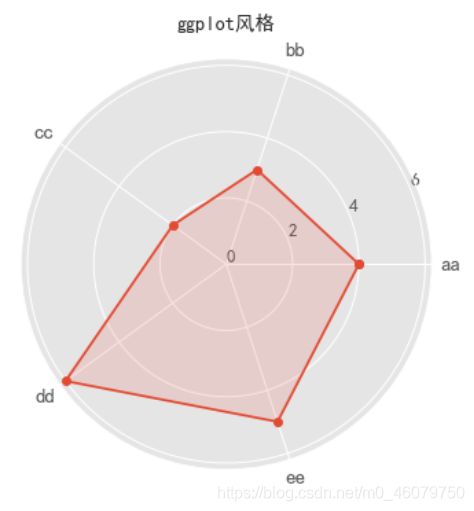
plt.title('seaborn风格')
plt.show()

最后再讲一下雷达图有什么用，举2个例子就明白了：

• 假如你是个老师，你要了解班上某个同学是否偏科或偏科是否严重，就可以把他（她）各科成绩绘制成雷达图，观察是否偏向某一科；
• 又如，你想要了解某个学生最近这段时间整体水平是进步还是退步，可以把他（她）最近的考试和前段时间考试的各科成绩用雷达图绘在一张图上，对比一下就知道了。

总之呢，我认为雷达图比较适合表现整体水平，以及反映各部分之间的关系。
终于ok了，雷达图就先介绍到这里。