抱抱仓鼠叭
抱抱仓鼠叭

洛谷线段树题解

基础题链接：https://blog.csdn.net/qq_48344603/article/details/107746383

P3372 【模板】线段树 1

洛谷线段树题解_第1张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 5;
ll tree[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
int n, m;
void buildtree(int left,int right,int r) {
     
	if (left == right) {
     
		tree[r] = num[left];
		return;
	}
	int mid = (left + right) / 2;
	buildtree(left, mid, 2 * r);
	buildtree(mid + 1,right, 2 * r + 1);
	tree[r] = tree[2 * r] + tree[2 * r + 1];
}
void push_down(ll left,ll right, int u) {
     
	ll len = right - left + 1;
	tree[2 * u] += add[u] * (len - len / 2);
	tree[2 * u + 1] += add[u] * (len / 2);
	add[2 * u] += add[u];
	add[2 * u + 1] += add[u];
	add[u] = 0;
}
void update(ll l, ll r, ll tar, int left, int right, int u) {
     
	if (left >= l && right <= r) {
     
		tree[u] += tar * (right - left + 1);
		add[u] += tar;
		return;
	}
	if (add[u]) {
     
		push_down(left, right, u);
	}
	int mid = (left + right) / 2;
	if (l <= mid)update(l, r, tar, left, mid, 2 * u);
	if (r > mid)update(l, r, tar, mid + 1, right, 2 * u + 1);
	tree[u] = tree[2 * u] + tree[2 * u + 1];
}
ll query(ll l, ll r, int left, int right, int u) {
     
	if (l <= left && r >= right) {
     
		return tree[u];
	}
	if (add[u]) {
     
		push_down(left, right, u);
	}
	int mid = (left + right) / 2;
	ll sum = 0;
	if (l <= mid)sum += query(l, r, left, mid, 2 * u);
	if (r > mid)sum += query(l, r, mid + 1, right, 2 * u + 1);
	return sum;
	
}
int main(){
     
	ios::sync_with_stdio(false);
	cin >> n >> m;
	for (int i = 1;i <= n;i++) {
     
		cin >> num[i];
	}
	buildtree(1, n, 1);
	for (int i = 1;i <= m;i++) {
     
		int c;
		cin >> c;
		if (c == 1) {
     
			ll left, right, tar;
			cin >> left >> right >> tar;
			update(left, right, tar, 1, n, 1);
		}
		if (c == 2) {
     
			ll left,right;
			cin >> left >> right;
			cout << query(left, right, 1, n, 1) << endl;
		}
	}
	return 0;
}

P3373 【模板】线段树 2

洛谷线段树题解_第2张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 5;
ll tree[MAXN * 4];
ll mul[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
int n, m, p;
//大部分都可以看题解
void push_down(int left, int right, int u) {
     
	int len = right - left + 1;
	tree[u << 1] = tree[u << 1] * mul[u] % p + add[u] * (len - len / 2);
	tree[u << 1] %= p;
	tree[u << 1 | 1] = tree[u << 1 | 1] * mul[u] % p + add[u] * (len / 2);
	tree[u << 1 | 1] %= p;
	mul[u << 1] *= mul[u], mul[u << 1] %= p;
	mul[u << 1 | 1] *= mul[u], mul[u << 1 | 1] %= p;
	//这部分做一些解释
	//为何在左右子树的add里也要乘上mul，不是在mul操作时已经改了嘛？
	//其实这2个操作不同，update2的操作只是对当前树的操作，而这里是对子树的操作，假设原来的子树就有add，现在我们从root往下down时，我们的mul只是把root的add操作了，并未对子树的add操作。
	add[u << 1] = add[u << 1] * mul[u] + add[u];
	add[u << 1 | 1] = add[u << 1 | 1] * mul[u] + add[u];
	add[u << 1 | 1] %= p;
	add[u << 1] %= p;
	add[u] = 0;
	mul[u] = 1;
}
void buildtree(int left, int right, int u) {
     
	if (left == right) {
     
		tree[u] = num[left];
		return;
	}
	int mid=(left + right) / 2;
	buildtree(left, mid, 2 * u);
	buildtree(mid+1,right, 2 * u + 1);
	tree[u] = (tree[2 * u] + tree[2 * u + 1]) %p;
}
void update1(ll l, ll r, ll tar, int left, int right, int u) {
     
	if (l <= left && r >= right) {
     
		tree[u] = (tree[u] + tar * (right - left + 1))%p;
		add[u] += tar;
		add[u] %= p;
		return;
	}
	push_down(left, right, u);
	int mid = (left + right) / 2;
	if (l <= mid)update1(l,r, tar, left,mid, u<<1);
	if (r > mid)update1(l,r, tar, mid+1,right, u << 1 | 1);
	tree[u] = tree[u << 1] + tree[u << 1 | 1];
	tree[u] %= p;
}
void update2(ll l, ll r, ll tar, int left, int right, int u) {
     
	if (l <= left && r >= right) {
     
	//这是乘法分配律
		add[u] *= tar;
		add[u] %= p;
		tree[u] *= tar;
		tree[u] %= p;
		mul[u] *= tar;
		mul[u] %= p;
		return;
	}
	push_down(left, right, u);
	int mid = (left + right) / 2;
	if (l <= mid)update2(l, r, tar, left, mid, u << 1);
	if (r > mid)update2(l, r, tar, mid + 1, right, u << 1 | 1);
	tree[u] = tree[u << 1] + tree[u << 1 | 1];
	tree[u] %= p;
}

ll query(ll l,ll r,int left, int right, int u) {
     
	if (l <= left && r >= right) {
     
		return tree[u];
	}
	push_down(left, right, u);
	int mid = (left + right) / 2;
	ll sum = 0;
	if (l <= mid)sum = (sum + query(l, r, left, mid, u << 1))%p;
	if (r > mid)sum = (sum + query(l, r, mid + 1, right, u << 1 | 1)) % p;
	return sum;
}
int main() {
     
	ios::sync_with_stdio(false);
	cin >> n >> m >> p;
	for (int i = 1;i <= 4 * n;i++)mul[i] = 1;
	for (int i = 1;i <= n;i++) {
     
		cin >> num[i];
		num[i] %= p;
	}
	buildtree(1, n, 1);
	for (int i = 1;i <= m;i++) {
     
		int c;
		cin >> c;
		if (c == 1) {
     
			ll l, r, tar;
			cin >> l >> r >> tar;
			update2(l, r, tar, 1, n, 1);
		}
		if (c == 2) {
     
			ll l, r, tar;
			cin >> l >> r >> tar;
			update1(l, r, tar, 1, n, 1);
		}
		if (c == 3) {
     
			ll l, r;
			cin >> l >> r;
			cout << query(l, r, 1, n, 1) << endl;
		}
	}
	return 0;
}

P2023 [AHOI2009] 维护序列

洛谷线段树题解_第3张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 5;
ll tree[MAXN * 4];
ll mul[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
int n, m, p;
//和2相同
void push_down(int left,int right,int u) {
     
	int len = (right - left + 1);
	tree[u << 1] = (tree[u << 1]*mul[u] + add[u] * (len-len/2)) % p;
	tree[u << 1 | 1] = (tree[u << 1 | 1] * mul[u] + add[u] * (len / 2)) % p;
	mul[u << 1] = (mul[u << 1] * mul[u]) % p;
	mul[u << 1 | 1] = (mul[u << 1 | 1] * mul[u]) % p;
	add[u << 1] = (add[u << 1] * mul[u] + add[u]) % p;
	add[u << 1|1] = (add[u << 1|1] * mul[u] + add[u]) % p;
	mul[u] = 1;
	add[u] = 0;
}
void buildtree(int left, int right, int u) {
     
	if (left == right) {
     
		tree[u] = num[left];
		return;
	}
	int mid = (left + right) >> 1;
	buildtree(left, mid, u << 1);
	buildtree(mid + 1, right, u << 1 | 1);
	tree[u] = (tree[u << 1] + tree[u << 1 | 1])%p;
}
void update1(ll l, ll r,ll tar, int left, int right, int u) {
     
	if (l <= left && r >= right) {
     
		add[u] *= tar;
		add[u] %= p;
		tree[u] *= tar;
		tree[u] %= p;
		mul[u] *= tar;
		mul[u] %= p;
		return;
	}
	push_down(left,right,u);
	int mid = (left + right)>>1;
	if (l <= mid)update1(l, r, tar, left, mid, u << 1);
	if (r > mid)update1(l, r, tar, mid + 1, right, u << 1 | 1);
	tree[u] = (tree[u << 1] + tree[u << 1 | 1]) % p;
}
void update2(ll l, ll r, ll tar, int left, int right, int u) {
     
	if (l <= left && r >= right) {
     
		tree[u] += tar * (right - left + 1);
		tree[u] %= p;
		add[u] += tar;
		add[u] %= p;
		return;
	}
	push_down(left,right,u);
	int mid = (left + right) >> 1;
	if (l <= mid)update2(l, r, tar, left, mid, u << 1);
	if (r > mid)update2(l, r, tar, mid + 1, right, u << 1 | 1);
	tree[u] = (tree[u << 1] + tree[u << 1 | 1]) % p;
}
ll query(ll l, ll r, int left, int right, int u) {
     
	if (l <= left && r >= right) {
     
		return tree[u];
	}
	push_down(left, right, u);
	int mid = (left + right) >> 1;
	ll sum = 0;
	if (l <= mid)sum =(sum+ query(l, r, left, mid, u << 1))%p;
	if (r > mid)sum =(sum+ query(l, r, mid + 1, right, u << 1 | 1))%p;
	return sum%p;
}
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> p;
	for (int i = 1;i <= 4 * n;i++)mul[i] = 1;
	for (int i = 1;i <= n;i++) {
     
		cin >> num[i];
		num[i] %= p;
	}
	buildtree(1, n, 1);
	cin >> m;
	for (int i = 1;i <= m;i++) {
     
		int c;
		cin >> c;
		if (c == 1) {
     
			ll l, r, tar;
			cin >> l >> r >> tar;
			update1(l, r, tar, 1, n, 1);
		}
		if (c == 2) {
     
			ll l, r, tar;
			cin >> l >> r >> tar;
			update2(l, r, tar, 1, n, 1);
		}
		if (c == 3) {
     
			int l, r;
			cin >> l >> r;
			cout << query(l, r, 1, n, 1) << endl;
		}
	}
	return 0;
}

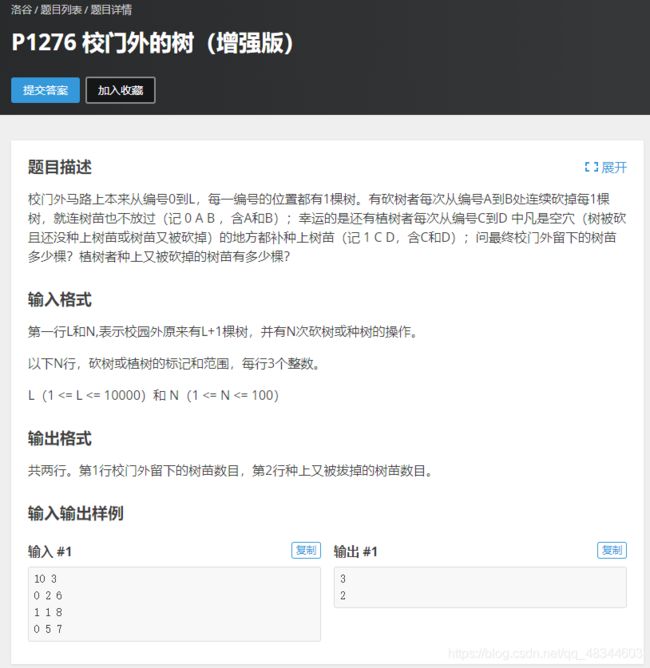
P1276 校门外的树（增强版）

洛谷线段树题解_第4张图片

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e4 + 5;
ll tree[MAXN * 4];
ll mul[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
int n, m;
int ans1=0, ans2=0;
//染色类线段树，注意区间时从0到n，而不是一般的从1到n
void update_cut(int l, int r, int left, int right, int rt) {
     
	int mid = (left + right) / 2;
	if (tree[rt] != 1 && tree[rt] != -1) {
     //push_down
		tree[rt << 1] = tree[rt << 1 | 1] = tree[rt];
	}
	if (l <= left && r >= right) {
     
		if (tree[rt] == 0)return;//树为0表示子树都被砍了
		else if (tree[rt] == 1) {
     //为1就砍
			tree[rt] = 0;
		}
		else if (tree[rt] == 2) {
     //为2计算
			ans1 += (right - left + 1);
			ans2 = ans2 - (right - left + 1);
			tree[rt] = 0;
		}
		else if (tree[rt] == -1) {
     
			tree[rt] = 0;
			if(l<=mid)update_cut(l, r, left, mid, rt<<1);
			if (r > mid)update_cut(l, r, mid + 1, right, rt << 1 | 1);
		}
	}
	else {
     
		if (l <= mid)update_cut(l, r, left, mid, rt << 1);
		if (r > mid)update_cut(l, r, mid + 1, right, rt << 1 | 1);
		if (tree[rt << 1] == tree[rt << 1 | 1])tree[rt] = tree[rt << 1];
		else tree[rt] = -1;
	}
}
void update_plant(int l, int r, int left, int right, int rt) {
     
	if (tree[rt] != 1 && tree[rt] != -1) {
     
		tree[rt << 1] = tree[rt << 1 | 1] = tree[rt];
	}
	int mid = (left + right) >> 1;
	if (l <= left && r >= right) {
     
		if (tree[rt] == 1 || tree[rt] == 2)return;
		if (tree[rt] == 0) {
     
			tree[rt] = 2;
			ans2 += right - left + 1;
		}
		if (tree[rt] == -1) {
     //树也可能是1
			if (l <= mid)update_plant(l, r, left, mid, rt << 1);
			if (r > mid)update_plant(l, r, mid + 1, right, rt << 1 | 1);
			if (tree[rt << 1] == tree[rt << 1 | 1]) {
     
				tree[rt] = tree[rt << 1];
			}
			else tree[rt] = -1;
		}
	}
	else {
     
		if (l <= mid)update_plant(l, r, left, mid, rt << 1);
		if (r > mid)update_plant(l, r, mid + 1, right, rt << 1 | 1);
		if (tree[rt << 1] == tree[rt << 1 | 1]) {
     
			tree[rt] = tree[rt << 1];
		}
		else tree[rt] = -1;
	}
}
void swap(int l, int r) {
     
	int tmp = l;
	l = r;
	r = tmp;
}
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m;
	for (int i = 0;i <= 4 * n;i++)tree[i] = 1;
	for (int i = 1;i <= m;i++) {
     
		int c;
		cin >> c;
		if (c == 1) {
     
			int l, r;
			
			cin >> l >> r;
			if (l > r)swap(l, r);
			update_plant(l, r, 0, n, 1);
		}
		if (c == 0) {
     
			int l, r;
			cin >> l >> r;
			if (l > r)swap(l, r);
			update_cut(l, r, 0, n, 1);
		}

	}
	cout << ans2 << endl;
	cout << ans1 << endl;
	return 0;
}

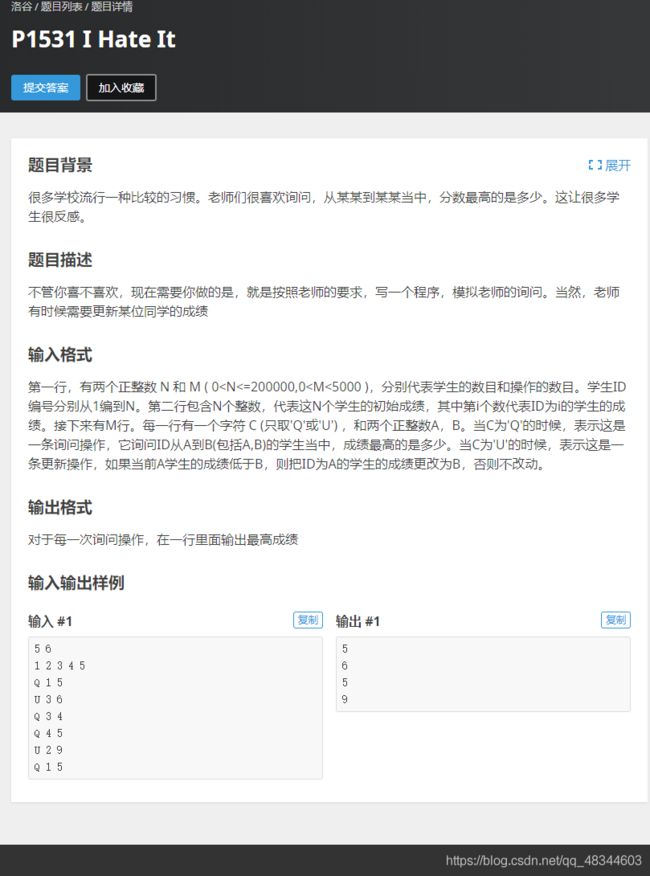
P1531 I Hate It

洛谷线段树题解_第5张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 5;
ll tree[MAXN * 4];
ll mul[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
int p[MAXN];
int n, m;
//单点修改+区间查询模板
void buildtree(int left, int right, int rt) {
     
	if (left == right) {
     
		tree[rt] = num[left];
		p[left] = rt;
		return;
	}
	int mid = (left + right) >> 1;
	buildtree(left, mid, rt << 1);
	buildtree(mid + 1, right, rt << 1 | 1);
	tree[rt] = max(tree[rt << 1], tree[rt << 1 | 1]);
}
void update(int pos, int tar, int left, int right, int rt) {
     
	if (left == right) {
     
		if (tree[rt] < tar) {
     
			tree[rt] = tar;
			
		}return;
	}
	int mid = (left + right) >> 1;
	if (pos <= mid)update(pos, tar, left, mid, rt << 1);
	else update(pos, tar, mid + 1, right, rt << 1 | 1);
	tree[rt] = max(tree[rt << 1], tree[rt << 1 | 1]);
}
int query(int l, int r,int left,int right,int rt) {
     
	if (l <= left && r >= right) {
     
		return tree[rt];
	}
	int mid = (left + right) >> 1;
	int maxn = 0;
	if (l <= mid)maxn = max(maxn, query(l, r, left, mid, rt << 1));
	if (r > mid)maxn = max(maxn, query(l, r, mid + 1, right, rt << 1 | 1));
	return maxn;
}
int main() {
     
	cin >> n >> m;
	for (int i = 1;i <= n;i++) {
     
		cin >> num[i];
	}
	buildtree(1, n, 1);
	char ch;
	for (int i = 1;i <= m;i++) {
     
		cin >> ch;
		if (ch == 'Q') {
     
			int l, r;
			cin >> l >> r;
			cout << query(l, r, 1, n, 1) << endl;
		}
		if (ch == 'U') {
     
			int l, r;
			cin >> l >> r;
			update(l, r, 1, n, 1);
		}
	}
	return 0;
}

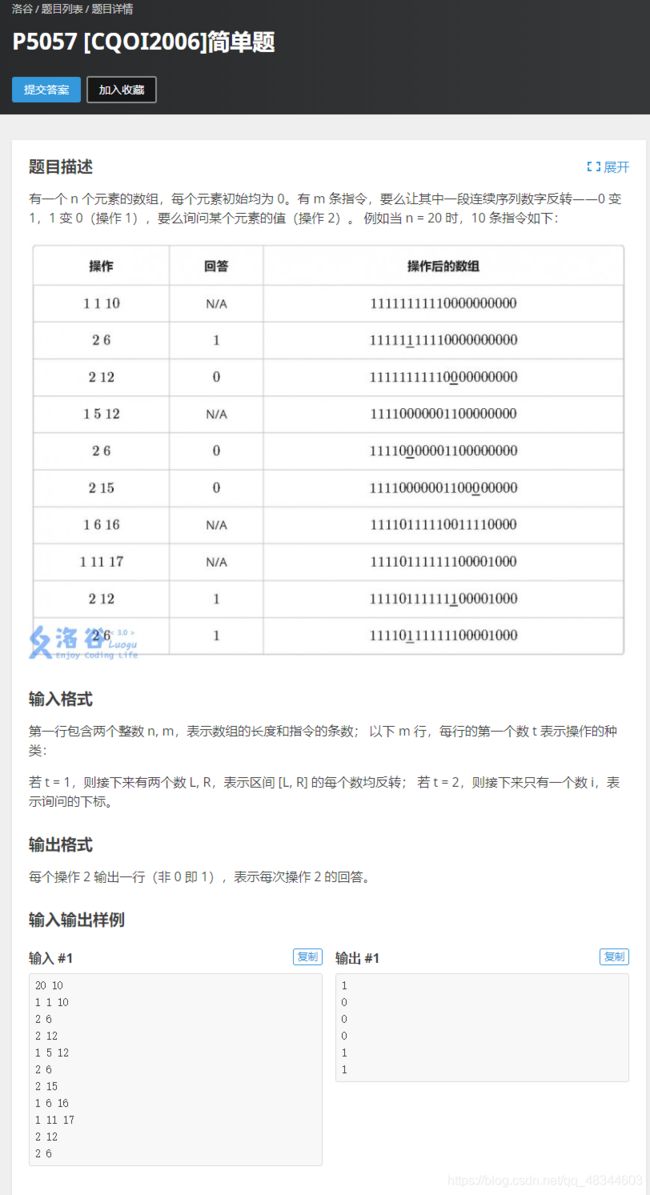
P5057 [CQOI2006]简单题

洛谷线段树题解_第6张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 5;
ll tree[MAXN * 4] = {
      0 };
ll mul[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
int p[MAXN];
int n, m;
void push_down(int rt) {
     
	tree[rt << 1] ^= 1;
	tree[rt << 1 | 1] ^= 1;
	tree[rt] = 0;
	return;
}
void update(int l, int r, int left, int right, int rt) {
     
	if (l <= left && r >= right) {
     
		tree[rt] ^= 1;
		return;
	}
	if (tree[rt]) {
     
		push_down(rt);
	}
	int mid = (left + right) >> 1;
	if (l <= mid)update(l, r, left, mid, rt << 1);
	if (r > mid)update(l, r, mid + 1, right, rt << 1 | 1);
}
int query(int pos, int left, int right, int rt) {
     
	if (left == right)return tree[rt];
	if (tree[rt]) {
     
		push_down(rt);
	}
	int mid = (left + right) >> 1;
	if (pos <= mid)return query(pos, left, mid, rt << 1);
	else return query(pos, mid + 1, right, rt << 1 | 1);
}
int main() {
     
	cin >> n >> m;
	for (int i = 1;i <= m;i++) {
     
		int c;
		cin >> c;
		if (c == 1) {
     
			int l, r;
			cin >> l >> r;
			update(l, r, 1, n, 1);
		}
		if (c == 2) {
     
			int pos;
			cin >> pos;
			cout<<query(pos, 1, n, 1)<<endl;
		}
	}
	return 0;
}

P4588 [TJOI2018]数学计算

洛谷线段树题解_第7张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 5;
ll tree[MAXN * 4];
ll mul[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
int n, m;
int cnt = 0;
//可能是因为在线段树专题上，这题并没有那么难，但是这种题目很容易想到逆元
//对于线段树就是1和2的单点修改，1是乘上num[pos],2是化为1
void update(ll pos, int left, int right, int rt,int c) {
     
	if (left == right) {
     
		if (c == 1) {
     
			tree[rt] *= num[pos];
			tree[rt] %= m;
		}
		else {
     
			tree[rt] =1;
		}
		return;
	}
	int mid = (left + right) >> 1;
	if (pos <= mid)update(pos, left, mid, rt << 1,c);
	else update(pos, mid + 1, right, rt << 1 | 1,c);
	tree[rt] = (tree[rt << 1] * tree[rt << 1 | 1] % m);
}
int main() {
     
	std::ios::sync_with_stdio(false);
	int t;
	cin >> t;
	while (t--) {
     
		cin >> n >> m;
		memset(num, 0, sizeof num);
		memset(tree, 0, sizeof tree);
		cnt = 0;
		for (int i = 1;i <= n * 4;i++)tree[i] = 1;
		for (int i = 1;i <= n;i++) {
     
			int c;
			cin >> c;
			if (c == 1) {
     
				cin >> num[++cnt];
				update(cnt, 1, n, 1, 1);
				cout << tree[1] << endl;
			}
			if (c == 2) {
     
				cin >> num[++cnt];
				update(num[cnt], 1, n, 1, 2);
				cout << tree[1] << endl;
			}
		}
	}
	return 0;
}

P1908 逆序对

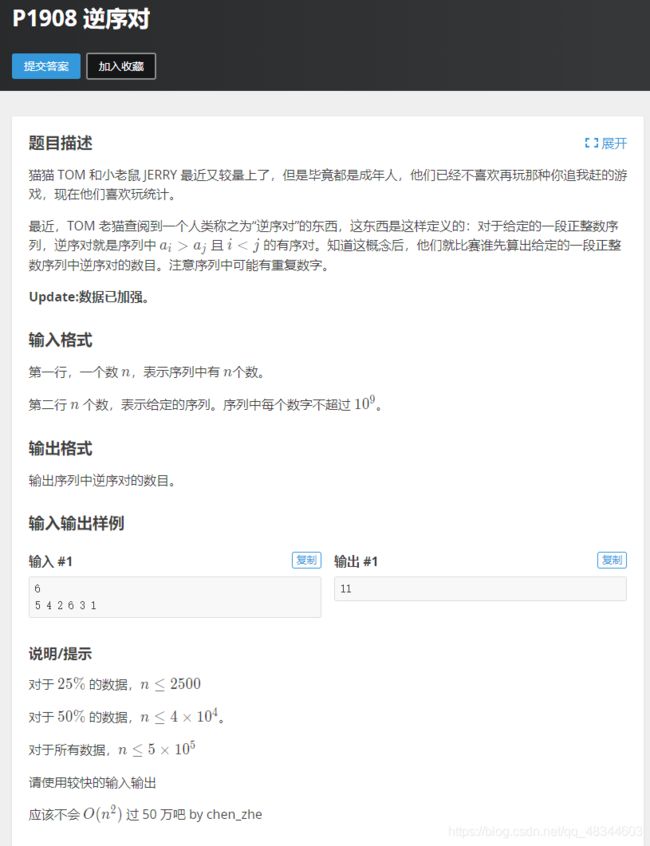
洛谷线段树题解_第8张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 5e5 + 5;
ll tree[MAXN * 4];
ll mul[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
ll b[MAXN];
int n, m;
void update(ll pos, int left, int right, int rt) {
     
	if (left == right) {
     
		tree[rt] ++;
		return;
	}
	int mid = (left + right) >> 1;
	if (pos <= mid)update(pos, left, mid, rt << 1);
	else update(pos, mid + 1, right, rt << 1 | 1);
	tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}
ll query(ll l, ll r, int left, int right, int rt) {
     
	if (l <= left && r >= right) {
     
		return tree[rt];
	}
	int mid = (left + right) >> 1;
	ll sum = 0;
	if (l <= mid)sum += query(l, r, left, mid, rt << 1);
	if (r > mid)sum += query(l, r, mid + 1, right, rt << 1 | 1);
	return sum;
}
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n;
	ll ans = 0;
	for (int i = 1;i <= n;i++) {
      
		cin >> num[i]; 
		b[i] = num[i];
	}
	//下面4行是离散化，因为数据为1e9，我们直接开线段树肯定不行，所以离散化
	sort(b + 1, b + 1 + n);//先对复制数组进行排序
	int sz = unique(b + 1, b + 1 + n) - b-1;//unique函数是对相邻相同的值伪去除，实际上是把相同的放到数组末尾，所以数组大小并没有改变，并且unique返回的是“去除”后的数组的尾位置，所以我们减去b-1可以得到不重复数组的长度
	for (int i = 1;i <= n;i++) {
     //对原数组进行离散化
		num[i] = lower_bound(b + 1, b + 1 + sz, num[i]) - b;//用lower_bound，在b数组中找到第一个小于等于num的数，为何减b，其实是减b+1，再+1，减去b+1得到第一个小于等于num数的位置，比如数组3 6 5 6 5 3 2 1，得到的值为2 4 3 4 3 2 1 0 所以我们+1，得到3 5 4 5 4 3 2 1
	}
	for (int i = n;i >= 1;i--) {
     
		update(num[i], 1, n, 1);
		if (num[i] == 1)continue;//1是最小的，防止下面num-1是的程序错误
		ans += query(1, num[i] - 1, 1, n, 1);
	}
	cout << ans << endl;
	return 0;
}

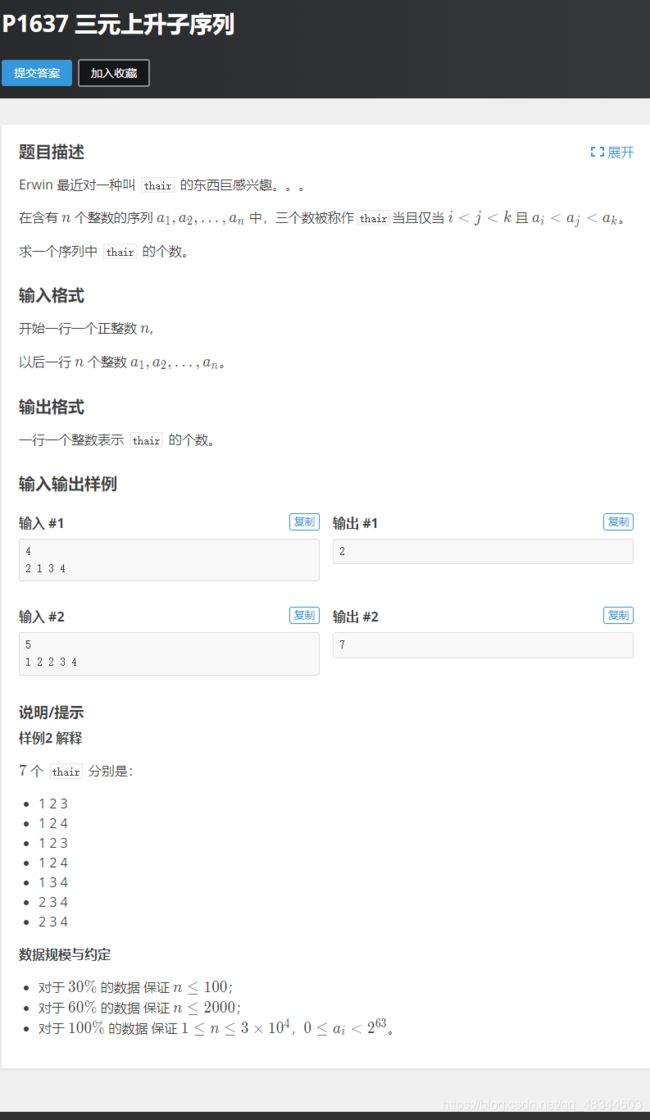
P1637 三元上升子序列

洛谷线段树题解_第9张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 5e5 + 5;
ll tree[MAXN * 4];
ll mul[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
ll b[MAXN];
ll sm[MAXN];
ll bi[MAXN];
int n, m;
//2次逆序数，分别都是求一个数前面比他小的，和后面比他大的，因为数据为2的31次方，很大，所以我们离散化
void update(ll pos, int left, int right, int rt) {
     
	if (left == right) {
     
		tree[rt]++;
		return;
	}
	int mid = (left + right) >> 1;
	if (pos <= mid)update(pos, left, mid, rt << 1);
	else update(pos, mid + 1, right, rt << 1 | 1);
	tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}
ll query(ll l, ll r, int left, int right, int rt) {
     
	if (l <= left && r >= right) {
     
		return tree[rt];
	}
	int mid = (left + right) >> 1;
	ll sum = 0;
	if (l <= mid)sum += query(l, r, left, mid, rt << 1);
	if (r > mid)sum += query(l, r, mid + 1, right, rt << 1 | 1);
	return sum;
}
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n;
	for (int i = 1;i <= n;i++) {
     
		cin >> num[i];
		b[i] = num[i];
	}
	sort(b + 1, b + 1 + n);
	int sz = unique(b + 1, b + 1 + n) - b - 1;
	for (int i = 1;i <= n;i++) {
     
		num[i] = lower_bound(b + 1, b + 1 + sz, num[i]) - b;
	}
	for (int i = 1;i <= n;i++) {
     
		if (num[i] == 1) {
     
			update(num[i], 1, n, 1);
			continue;
		}
		sm[i] = query(1, num[i] - 1, 1, n, 1);
		update(num[i], 1, n, 1);
	}
	memset(tree, 0, sizeof tree);
	for (int i = n;i >= 1;i--) {
     
		if (num[i] == sz) {
     
			update(num[i], 1, n, 1);
			continue;
		}
		bi[i] = query(num[i] + 1, sz, 1, n, 1);
		update(num[i], 1, n, 1);
	}
	ll ans = 0;
	//cout << sz << endl;
	for (int i = 1;i <= n;i++) {
     
		//cout << i << " " <
		ans += sm[i] * bi[i];
	}
	cout << ans << endl;
	return 0;
}

P6492 [COCI2010-2011#6] STEP

洛谷线段树题解_第10张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 5;
ll tree[MAXN * 4];
ll maxseg[MAXN * 4];
ll lmax[MAXN * 4], rmax[MAXN * 4];
bool L[MAXN * 4], R[MAXN * 4];
ll mul[MAXN * 4];
ll add[MAXN * 4];
ll num[MAXN];
ll len[MAXN * 4];
int n, m;
//这题也算经典类型的线段树，要维护多个区间值
void build(int left,int right,int rt) {
     //主要为了得到每个区间的长度
	len[rt] = right - left + 1; 
	if (left == right) {
      return; }
	int mid = (left + right) >> 1;
	build(left, mid, rt << 1);
	build(mid + 1, right, rt << 1 | 1);
}
void push_up(int left,int right,int rt) {
     
	if (R[rt << 1] ^ L[rt << 1 | 1]) {
     //如果左右子树的相接的点不同
		maxseg[rt] = rmax[rt << 1] + lmax[rt << 1 | 1];//这里必须是赋值，不能改为max（maxseg，rmax+lmax），因为有时候update后，maxseg会减少，如果max的话，就不会了
		maxseg[rt] = max(maxseg[rt], maxseg[rt << 1]);
		maxseg[rt] = max(maxseg[rt], maxseg[rt << 1 | 1]);
	}
	else maxseg[rt] = max(maxseg[rt << 1], maxseg[rt << 1 | 1]);
	if (lmax[rt << 1] ==len[rt<<1] && R[rt << 1] ^ L[rt << 1 | 1]) {
     //更改包含左结点的最大长度
		lmax[rt] = lmax[rt << 1] + lmax[rt << 1 | 1];
	}
	else {
     
		lmax[rt] = lmax[rt << 1];
	}
	if (rmax[rt << 1 | 1] == len[rt << 1 | 1] && R[rt << 1] ^ L[rt << 1 | 1]) {
     //包含右节点的最大长度
		rmax[rt] = rmax[rt << 1 | 1] + rmax[rt << 1];
	}
	else rmax[rt] = rmax[rt << 1 | 1];
	L[rt] = L[rt << 1];
	R[rt] = R[rt << 1 | 1];//更新左右结点
}
void update(int pos, int left, int right, int rt) {
     
	if (left == right) {
     
		L[rt] = R[rt] = !L[rt];
		return;
	}
	int mid = (left + right) >> 1;
	if (pos <= mid)update(pos, left, mid, rt << 1);
	else update(pos, mid + 1, right, rt << 1 | 1);
	push_up(left,right,rt);
	//cout << rt << " " << left << " " << right << " " << maxseg[rt] << endl;
}
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m;
	build(1, n, 1);
	for (int i = 1;i <= 4 * n;i++) {
     
		maxseg[i] = 1;
		L[i] = R[i] = 0;
		lmax[i] = rmax[i] = 1;
	}
	for (int i = 1;i <= m;i++) {
     
		int pos;
		cin >> pos;
		update(pos, 1, n, 1);
		cout << maxseg[1] << endl;
	}
	return 0;
}

P2894 [USACO08FEB]Hotel G

洛谷线段树题解_第11张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 5;
ll tree[MAXN * 4];
ll maxseg[MAXN * 4];
ll lmax[MAXN * 4], rmax[MAXN * 4];
bool L[MAXN * 4], R[MAXN * 4];
ll mul[MAXN * 4];
ll lazy[MAXN * 4];
ll num[MAXN];
ll len[MAXN * 4];
int n, m;
//这题我们要维护子树包含左端点最大值，包含右端点最大值，区间最大值
void buildtree(int left, int right, int rt) {
     
	len[rt]=maxseg[rt] = rmax[rt] = lmax[rt] = right - left + 1;
	if (left == right)return;
	int mid = (left + right) >> 1;
	buildtree(left, mid, rt << 1);
	buildtree(mid+1, right, rt << 1 | 1);
}
void push_up(int rt) {
     //这里push_up用来更新rt结点
	if (lmax[rt << 1] == len[rt << 1]) {
     //下面3步为正常的区间维护最值
		lmax[rt] = lmax[rt << 1] + lmax[rt << 1 | 1];
	}
	else lmax[rt] = lmax[rt << 1];
	if (rmax[rt << 1 | 1] == len[rt << 1 | 1]) {
     
		rmax[rt] = rmax[rt << 1 | 1] + rmax[rt << 1];
	}
	else rmax[rt] = rmax[rt << 1|1];
	maxseg[rt] = max(max(rmax[rt << 1] + lmax[rt << 1 | 1], maxseg[rt << 1]), maxseg[rt << 1 | 1]);
}
void push_down(int rt) {
     
	if (lazy[rt]) {
     
		if (lazy[rt] == 1) {
     
			maxseg[rt << 1] = maxseg[rt << 1 | 1] = 0;
			rmax[rt << 1] = lmax[rt << 1] = rmax[rt << 1 | 1] = lmax[rt << 1 | 1] = 0;
			lazy[rt << 1] = lazy[rt << 1 | 1] = 1;
		}
		else {
     
			maxseg[rt << 1] = rmax[rt << 1] = lmax[rt << 1] = len[rt<<1];
			maxseg[rt << 1 | 1] = lmax[rt << 1 | 1] = rmax[rt << 1 | 1] = len[rt << 1 | 1];
			lazy[rt << 1] = lazy[rt << 1 | 1] = 2;
		}
		lazy[rt] = 0;
	}
}
void update(int l, int r, int left, int right, int rt, int tag) {
     
	
	int mid = (left + right) >> 1;
	if (l <= left && r >= right) {
     //正常区间修改，只是这里判断tag
		if (tag == 1) {
     
			maxseg[rt] = lmax[rt] = rmax[rt] = 0;
			lazy[rt] = 1;
		}
		else {
     
			maxseg[rt] = lmax[rt] = rmax[rt] = len[rt];
			lazy[rt] = 2;
		}
		return;
	}
	push_down(rt);//如果不满足上面的if，我们就要进行拆开update，所以要push——down
	if (l <= mid)update(l, r, left, mid, rt << 1, tag);
	if (r > mid)update(l, r, mid + 1, right, rt << 1 | 1, tag);
	push_up(rt);//对于2个子树我们update后，我们要对root结点进行改变
}
int query(int tar, int left, int right, int rt) {
     
	push_down(rt);
	if (left == right)return left;
	int mid = (left + right) >> 1;
	if (maxseg[rt << 1] >= tar)return query(tar, left, mid, rt << 1);
	if (rmax[rt << 1] + lmax[rt << 1 | 1] >= tar)return mid - rmax[rt << 1] + 1;
	else return query(tar, mid + 1, right, rt << 1 | 1);
}
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m;
	buildtree(1, n, 1);
	for (int i = 1;i <= m;i++) {
     
		int c;
		cin >> c;
		if (c == 1) {
     
			int tar;
			cin >> tar;
			if (maxseg[1] >= tar) {
     
				int left = query(tar, 1, n, 1);
				cout << left << endl;
				update(left, left + tar-1, 1, n, 1, 1);
			}
			else cout << 0 << endl;

		}
		else {
     
			int left, leng;
			cin >> left >> leng;
			update(left, left + leng - 1, 1, n, 1, 2);
		}
		//cout << rmax[2] << " " << lmax[3] << endl;
		//cout << maxseg[3] << endl;
	}
	return 0;
}

P2184 贪婪大陆

洛谷线段树题解_第12张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 5;
ll tree[MAXN * 4];
ll maxseg[MAXN * 4];
ll lmax[MAXN * 4], rmax[MAXN * 4];
bool L[MAXN * 4], R[MAXN * 4];
ll mul[MAXN * 4];
ll lazy[MAXN * 4];
ll num[MAXN];
ll len[MAXN * 4];
int n, m;
bool visit[MAXN];
//这题属于叠加类的线段树，有点染色类线段树的意思，但是不一样，染色类表示自己对这个区间就直接实现覆盖，并且可能覆盖多种颜色
//但是这题并不是，这题是叠加，同样地方完全可以埋无数颗地雷
//那么这区间查询地雷怎么做，假设我们update（a，b），其中b为update的右端点，a为左端点，那么我们a到b区间就有1颗地雷，以外区间没有，那么我们query区间（x，y），我们对于1到x-1找update中右端点共有几个，对于y+1到n找左端点有几个（我们将这些总和，这些地雷保证埋不到区间x到y）。每次埋雷用cnt++，最后我们用cnt减去不埋在x到y的地雷，就是埋在x到y的地雷数
void update(int pos, int tag, int left, int right, int rt) {
     
	if (left == right) {
     
		if (tag == 1)lmax[rt]++;
		if (tag == 2)rmax[rt]++;
		return;
	}
	int mid=(left + right) >> 1;
	if (pos <= mid)update(pos, tag, left, mid, rt << 1);
	else update(pos, tag, mid + 1,right, rt << 1 | 1);
	if (tag == 1)lmax[rt] = lmax[rt << 1] + lmax[rt << 1 | 1];
	else rmax[rt] = rmax[rt << 1] + rmax[rt << 1 | 1];
}
int query(int l, int r, int tag,int left, int right, int rt) {
     
		if (l <= left && r >= right) {
     
			if (tag == 1)return lmax[rt];
			if (tag == 2)return rmax[rt];
		}
		int mid = (left + right) >> 1;
		int sum = 0;
		if (l <= mid)sum += query(l, r, tag, left, mid, rt << 1);
		if (r > mid)sum += query(l, r, tag, mid + 1, right, rt << 1 | 1);
		return sum;
	}
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m;
	int cnt = 0;
	for (int i = 1;i <= m;i++) {
     
		int c;
		cin >> c;
		if (c == 1) {
     
			cnt++;
			int l, r;
			cin >> l >> r;
			update(l, 1, 1, n, 1);
			update(r, 2, 1, n, 1);
		}
		if (c == 2) {
     
			int l, r;
			cin >> l >> r;
			int sum = 0;
			if (l >= 2)sum+=query(1, l - 1, 2, 1, n, 1);
			if (r <= n - 1)sum+=query(r + 1, n, 1, 1, n, 1);
			cout << cnt - sum << endl;
		}
	}
	return 0;
}

P1438 无聊的数列

洛谷线段树题解_第13张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 5;
ll tree[MAXN * 4];
ll maxseg[MAXN * 4];
ll lmax[MAXN * 4], rmax[MAXN * 4];
bool L[MAXN * 4], R[MAXN * 4];
ll mul[MAXN * 4];
ll lazy[MAXN * 4];
ll num[MAXN];
ll len[MAXN * 4];
int n, m;
bool visit[MAXN];
//一个区间加上等差数列，我们要想到差分，比如在l到r区间，我们用差分的话，在l到r区间加上等差数列，相当于在l加上K，在l+1到r加上D，在r+1处减去K+（l-r）*D
//我们用tree来维护差分值，num记录初始的数据
void push_down(int rt,int len) {
     
	if (lazy[rt]) {
     
		tree[rt << 1] += lazy[rt] * (len - len / 2);
		tree[rt << 1 | 1] += lazy[rt] * (len / 2);
		lazy[rt << 1] += lazy[rt];
		lazy[rt << 1 | 1] += lazy[rt];
		lazy[rt] = 0;
	}
}
void updatelr(int l, int r, int D, int left, int right, int rt) {
     
	if (l <= left && r >= right) {
     
		tree[rt] += D * (right - left + 1);
		lazy[rt] += D;
		return;
	}
	push_down(rt, right - left + 1);
	int mid = (left + right) >> 1;
	if (l <= mid)updatelr(l, r, D, left, mid, rt << 1);
	if (r > mid)updatelr(l, r, D, mid + 1, right, rt << 1 | 1);
	tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}
int query(int l,int r, int left, int right, int rt) {
     
	if (l <= left && r >= right) {
     
		return tree[rt];
	}
	push_down(rt, right - left + 1);
	int mid = (left + right) >> 1;
	int sum = 0;
	if (l <= mid)sum += query(l, r, left, mid, rt << 1);
	if (r > mid)sum += query(l, r, mid + 1, right, rt << 1 | 1);
	return sum;
}
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m;
	for (int i = 1;i <= n;i++) {
     
		cin >> num[i];
	}
	for (int i = 1;i <= m;i++) {
     
		int c;
		cin >> c;
		if (c == 1) {
     
			int l, r, K, D;
			cin >> l >> r >> K >> D;
			updatelr(l,l, K, 1, n, 1);
			
			if (r > l) {
     
				updatelr(l + 1, r, D, 1, n, 1);//如果r==l的话我们我们这一步不用操作
			}
			if(r!=n)updatelr(r + 1,r+1, -(K+(r-l)*D), 1, n, 1);//如果r==n的话，就不用再r+1
		}
		if (c == 2) {
     
			int r;
			cin >> r;
			cout << num[r]+query(1, r, 1, n, 1) << endl;
		}
	}
	return 0;
}

P4145 上帝造题的七分钟2 / 花神游历各国

洛谷线段树题解_第14张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 5;
ll tree[MAXN * 4];
ll maxseg[MAXN * 4];
ll lmax[MAXN * 4], rmax[MAXN * 4];
bool L[MAXN * 4], R[MAXN * 4];
ll mul[MAXN * 4];
ll lazy[MAXN * 4];
ll num[MAXN];
ll len[MAXN * 4];
int n, m;
bool visit[MAXN];
//这题属于每个数的更新次数有限制，一个数最多更新6次，所以，假设最后把每个数都更新一遍需要6e5的复杂度，我们返回sum总和，维护sum，nlogm，为何是logm呢，我们暴力修改单点不应该是nm复杂度嘛，所以我们还要维护区间最大值，如果区间最大值>1，我们需要修改，其他我们不用，这样我们就省去多余步骤，复杂度降低。
void swap(int& l, int& r) {
     
	int tmp = l;
	l = r;
	r = tmp;
}//防止l和r顺序不同
void buildtree(int left, int right, int rt) {
     
	if (left == right) {
     
		tree[rt] = num[left];
		maxseg[rt] = num[left];
		return;
	}
	int mid = (left + right) >> 1;
	buildtree(left, mid, rt << 1);
	buildtree(mid + 1, right, rt << 1 | 1);
	tree[rt] = tree[rt << 1] + tree[rt << 1|1];
	maxseg[rt] = max(maxseg[rt << 1], maxseg[rt << 1 | 1]);
}
void update(int l, int r, int left, int right, int rt) {
     
	if (left == right) {
     
		maxseg[rt] = tree[rt] = sqrt(maxseg[rt]);//单点暴力修改
		return;
	}
	int mid = (left + right) >> 1;
	if (l <= mid && maxseg[rt << 1] > 1)update(l, r, left, mid, rt << 1);
	if (r > mid && maxseg[rt << 1 | 1] > 1)update(l, r, mid + 1, right, rt << 1 | 1);
	maxseg[rt] = max(maxseg[rt << 1], maxseg[rt << 1 | 1]);
	tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}
ll query(int l, int r, int left, int right, int rt) {
     
	if (l <= left && r >= right) {
     
		return tree[rt];
	}
	int mid = (left + right) >> 1;
	ll sum = 0;
	if (l <= mid)sum += query(l, r, left, mid, rt << 1);
	if (r > mid)sum += query(l, r, mid + 1, right, rt << 1 | 1);
	return sum;
}
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n;
	for (int i = 1;i <= n;i++)cin >> num[i];
	buildtree(1, n, 1);
	cin >> m;
	for (int i = 1;i <= m;i++) {
     
		int c;
		cin >> c;
		if (c == 0) {
     
			int l, r;
			cin >> l >> r;
			if (l > r)swap(l, r);
			update(l, r, 1, n, 1);
		}
		if (c == 1) {
     
			int l, r;
			cin >> l >> r;
			if (l > r)  swap(l, r); 
			cout << query(l, r, 1, n, 1) << endl;
		}
	}
	return 0;
}

P6327 区间加区间sin和

洛谷线段树题解_第15张图片


#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 5;
ll tree[MAXN << 2];
ll maxseg[MAXN * 4];
double cose[MAXN << 2], sine[MAXN << 2];
ll lazy[MAXN * 4];
ll num[MAXN];
ll len[MAXN * 4];
int n, m;
bool visit[MAXN];
//这题是卡常数的题目，所以建议用快读
int read() {
     
	char c = getchar();int ans = 0;
	while (c < '0' || c>'9') c = getchar();
	while (c >= '0' && c <= '9') ans = (ans << 1) + (ans << 3) + (c ^ 48), c = getchar();
	return ans;
}
//改变sin与cos，我们用到sin(a+x)=sina*cosx+cosa*sinx以及cos(a+x)=cosa*cosx-sina*sinx
void buildtree(int left, int right, int rt) {
     
	if (left == right) {
     
		sine[rt] = sin(num[left]);
		cose[rt] = cos(num[left]);
		return;
	}
	int mid = (left + right) >> 1;
	buildtree(left, mid, rt << 1);
	buildtree(mid + 1, right, rt << 1 | 1);
	cose[rt] = cose[rt << 1] + cose[rt << 1 | 1];//这边用了乘法分配律，将拆开的sin与cos乘法分配
	sine[rt] = sine[rt << 1] + sine[rt << 1 | 1];
}
void push_down(int rt) {
     
	if (lazy[rt]) {
     
		double s = sin(lazy[rt]), c = cos(lazy[rt]);
		double s1 = sine[rt << 1], s2 = sine[rt << 1 | 1], c1 = cose[rt << 1], c2 = cose[rt << 1 | 1];//自己弄懂公式，这个也会懂
		sine[rt << 1] = s1 * c + c1 * s;
		sine[rt << 1 | 1] = s2 * c + c2 * s;
		cose[rt << 1] = c1 * c - s1 * s;
		cose[rt << 1 | 1] = c2 * c - s2 * s;
		lazy[rt << 1] += lazy[rt];
		lazy[rt << 1 | 1] += lazy[rt];
		lazy[rt] = 0;
	}
}
void update(int l, int r, int tar, int left, int right, int rt) {
     
	if (l <= left && r >= right) {
     
		double c = cose[rt], s = sine[rt];
		sine[rt] = sin(tar) * c + cos(tar) * s;
		cose[rt] = cos(tar) * c - sin(tar) * s;
		lazy[rt] += tar;
		return;
	}
	push_down(rt);
	int mid = (left + right) >> 1;
	if (l <= mid)update(l, r, tar,left, mid, rt << 1);
	if (r > mid)update(l, r,tar, mid + 1, right, rt << 1 | 1);
	sine[rt] = sine[rt << 1] + sine[rt << 1 | 1];//乘法分配
	cose[rt] = cose[rt << 1] + cose[rt << 1 | 1];
}
double query(int l, int r, int left, int right, int rt) {
     
	if (l <= left && r >= right) {
     
		return sine[rt];
	}
	push_down(rt);
	int mid = (left + right) >> 1;
	double sum = 0;
	if (l <= mid)sum += query(l, r, left, mid, rt << 1);
	if (r > mid)sum += query(l, r, mid + 1, right, rt << 1 | 1);
	return sum;
}
int main() {
     
	
	n = read();
	for (int i = 1;i <= n;i++)num[i] = read();
	buildtree(1, n, 1);
	m = read();
	for (int i = 1;i <= m;i++) {
     
		int c;
		c = read();
		if (c == 1) {
     
			int l, r, tar;
			l = read(), r = read(), tar = read();
			update(l, r, tar, 1, n, 1);
		}
		if (c == 2) {
     
			int l, r;
			l = read(), r = read();
			cout << fixed << setprecision(1) << query(l, r, 1, n, 1) << endl;
		}
	}
	return 0;
}

你可能感兴趣的:(算法入门,算法,图论)

  • 贪心算法：求过河的最短时间 2301_81758904 算法
    描述：N位旅行者在夜里过桥需要借助手电筒。但N个人中只有一个手电筒，而且桥同时只能让两个人过。每个人单独过桥所需时间已知，但如果两个人同时过桥则所需时间是走得慢的那个人单独过桥所需的时间。要求：设计一个方案，让这N个人尽快过桥，计算这N个人的最短过桥时间。此如：有甲乙丙丁四个人，他们过河所需的时间分别是1，2，5，10。让最快的2个人先过桥，然后让跑的最快的人回去接剩下的人。例如：先让甲乙过去(2
  • 常见哈希表相关题目 我要学编程(ಥ_ಥ) 优选算法专题算法数据结构哈希表
    找往期文章包括但不限于本期文章中不懂的知识点：个人主页：我要学编程(ಥ_ಥ)-CSDN博客所属专栏：优选算法专题目录1.两数之和面试题01.02.判定是否互为字符重排217.存在重复元素219.存在重复元素II49.字母异位词分组哈希表我们在数据结构阶段也是重点学习了，并且也已经刷了一部分的题目了。下面还练习一部分题目即可。1.两数之和题目：给定一个整数数组nums和一个整数目标值target，请
  • 华为OD机试E卷 --找数字--24年OD统一考试（Java & JS & Python & C & C++） 飞码创造者 最新华为OD机试题库2024华为odjavajavascriptc语言python
    文章目录题目描述输入描述输出描述用例题目解析JS算法源码Java算法源码python算法源码c算法源码c++算法源码题目描述小扇和小船今天又玩起来了数字游戏，小船给小扇一个正整数n（1≤n≤1e9），小扇需要找到一个比n大的数字m，使得m和n对应的二进制中1的个数要相同，如：4对应二进制1008对应二进制1000其中1的个数都为1个现在求m的最小值。输入描述输入一个正整数n（1≤n≤1e9）输出描
  • 机器学习：scikit-learn 和 Jupyter Notebook（推荐初学者使用google colab） wyc9999ww 机器学习scikit-learnjupyter人工智能python
    对于初学者来说，scikit-learn是一个理想的机器学习入门工具。不仅提供了丰富的算法和功能，还通过一致的API设计，确保能够快速上手并进行各种机器学习任务。通过使用scikit-learn，可以专注于理解和实践机器学习的核心概念，而不必过多担心底层实现细节。所以scikit-learn能轻松实现从数据预处理到模型训练和评估的完整流程。此外在推荐一个适合初学者的深度学习平台工具googleco
  • 使用Python解决数独谜题的实用指南 werf456456asddd python开发语言
    在这篇文章中，我们将探讨如何编写一个Python函数来解决数独谜题。这个函数将接收一个9x9的数独网格作为输入，并使用回溯算法来解决谜题。如果谜题无法解决，函数将返回None。此外，我们还会确保输入网格是一个有效的数独谜题。技术背景介绍数独是一种经典的逻辑游戏，目标是填满一个9x9的网格，使每列、每行和每个3x3的子网格都包含1到9之间的数字。在计算机科学中，数独可以通过回溯算法来求解，这是一种尝
  • 用大数据“喂养”出来的AI模型ChatGPT 爆火是大数据、大算力、强算法的支撑，中国缺乏的什么？ Ai17316391579 深度学习服务器人工智能
    先来了解一下ChatGPT的基本情况ChatGPT本质属于生成式人工智能，属于无监督或半监督的机器学习。与之相关的还有Discriminativemodeling区分式模型，区分式模型大多属于监督式学习。生成性人工智能目前有两种主要的框架：GAN（GenerativeAdversarialNetwork）和GPT（GenerativePre-trainedTransformer）。GAN目前广泛应
  • 国家统计局湖北调查总队副总队长张小青一行调研珈和科技农业遥感调查智能化算法 珈和info 科技
    1月15日上午，国家统计局湖北调查总队党组成员、副总队长张小青一行莅临珈和科技开展调研。调研期间，张小青一行实地了解了珈和科技在自动化作物分布提取技术领域的最新成果，深入探讨了作物自动化处理模型在农业调查上应用的创新价值及优化方向。双方就模型的区域适应性提升、精度优化等核心议题展开了深入交流。会上，张小青副总队长肯定了珈和作为高科技企业在农业遥感调查科技创新领域的探索，以及其数据算法模型在农业调查
  • 智能优化算法应用：堆优化算法优化脉冲耦合神经网络的图像自动分割 智能算法研学社（Jack旭） 智能优化算法应用图像分割算法神经网络人工智能
    智能优化算法应用：堆优化算法优化脉冲耦合神经网络的图像自动分割文章目录智能优化算法应用：堆优化算法优化脉冲耦合神经网络的图像自动分割1.堆优化算法2.PCNN网络3.实验结果4.参考文献5.Matlab代码摘要：本文利用堆优化算法对脉冲耦合神经网络的参数进行优化，以信息熵作为适应度函数，提高其图像分割的性能。1.堆优化算法堆优化算法原理请参考：https://blog.csdn.net/u0118
  • AI未来趋势：AIGC浪潮下看AI训练师如何塑造智能未来（技术变革） 用心去追梦 前端htmlcss
    在AIGC（AIGeneratedContent，人工智能生成内容）浪潮下，AI训练师扮演着至关重要的角色，他们不仅推动了技术的发展，还在确保这些技术能够安全、高效地服务于社会方面发挥了重要作用。以下是AI训练师如何塑造智能未来的几个关键方面：1.技术变革与创新算法与模型训练预训练：通过大规模无标注数据的学习，构建具备基础语言理解和生成能力的基座模型。这一过程为后续更精细的任务打下了坚实的基础。指
  • 深入理解AIGC背后的核心算法：GAN、Transformer与Diffusion Models 忘梓. 杂文AIGC算法生成对抗网络
    深入理解AIGC背后的核心算法：GAN、Transformer与DiffusionModels前言随着人工智能技术的发展，AIGC（AIGeneratedContent，人工智能生成内容）已经不再是科幻电影中的幻想，而成为了现实生活中的一种新兴力量。无论是自动生成文章、绘制图像、生成音乐还是创作视频，AIGC都在各个内容创作领域崭露头角。然而，这些“智能创作”的背后究竟依赖于哪些算法？今天，我们将
  • 哈希算法篇——散落的秘密与精准的归宿，混沌中的秩序之美（上） 诚丞成 常用算法讲解哈希算法算法
    文章目录引言：混沌中的秩序之美第一章：哈希的本质——化繁为简的魔法第二章：经典哈希函数——一座算法的博物馆第三章：哈希表的奇迹——从无序到有序的转变3.1哈希函数的基本实现3.2基本的哈希表实现3.3哈希算法的实际应用小结引言：混沌中的秩序之美在信息科学的星空下，有一种算法宛如一位洞悉混沌的智者，能够以其独特的规则，在无限的可能性中找到秩序。这便是哈希算法（HashingAlgorithm），一个
  • python分段线性插值_计算方法（3）——分段插值法（附Python程序） weixin_39900206 python分段线性插值
    在上一节计算方法(2)——插值法(附Python程序)当中，主要讲了插值法，介绍了龙格现象，并给出了插值法的代码。这一讲主要分段插值中的分段线性插值和分段Hermite插值，并给出分段插值的Python程序。在此之前需要注意一下，n为区间数，n+1为插值节点的个数。分段线性插值分段线性插值，需要两个列表，一个用于存放各点的x坐标，一个用于存放各点的y坐标。因为分段插值的算法需要x坐标按顺序增长，而
  • 如何使用 Python 实现简单的算法与数据结构 全栈探索者chen pythonpython算法数据结构开发语言javascript数据分析性能优化
    如何使用Python实现简单的算法与数据结构算法和数据结构是计算机科学的基础，理解它们不仅有助于解决复杂问题，还能提高编程效率和代码质量。在Python中，由于其简洁和高效的语法，学习和实现算法与数据结构更加轻松。本文将从以下几个方面探讨如何用Python实现常见的数据结构和基本算法，帮助你从基础开始掌握核心概念。一、数据结构1.数组（Array）数组是一种线性数据结构，存储一组相同类型的元素。P
  • 基于纵横交叉算法优化的最小交叉熵图像多阈值分割 python 图像算法打怪 图像分割算法python开发语言
    基于纵横交叉算法优化的最小交叉熵图像多阈值分割python文章目录基于纵横交叉算法优化的最小交叉熵图像多阈值分割python1.最小交叉熵阈值分割原理2.基于纵横交叉优化的多阈值分割3.算法结果：4.参考文献：5.Python代码摘要：本文介绍基于最小交叉熵的图像分割，并且应用纵横交叉算法进行阈值寻优。1.最小交叉熵阈值分割原理1993年，Li等人将交叉熵的概念引入到图像处理领域，提出了基于一维灰
  • 设计模式-策略模式 夏旭泽 设计模式策略模式
    背景有各种鸭子，野鸭、北京鸭、玩具鸭，有各个行为，比如飞、叫传统思路创建一个Duck父类，在这个父类中声明鸭子的共同行为与属性，所有鸭子继承自这个父类。问题：继承时，一些子类可能修改父类的大部分行为与属性，会有溢出效应。基本介绍定义一些算法族，分别封装起来，让他们之间可以相互替换。把算法封装成接口，聚合到使用类中把变化的代码从不变的代码中分离出来。用聚合和组合的方式代替继承。将使用层和算法实现层分
  • 路径规划：环境适应性路径规划_（7）.路径规划的不确定性处理 zhubeibei168 机器人（二）机器人计算机视觉机器人导航人工智能数码相机
    路径规划的不确定性处理在路径规划中，不确定性是一个常见的问题，尤其是在动态和复杂的环境中。不确定性可以来源于多种因素，包括传感器误差、环境变化、动态障碍物等。处理不确定性是确保路径规划算法在实际应用中能够稳定、可靠运行的关键。本节将详细探讨路径规划中的不确定性处理方法，包括概率模型、鲁棒优化、重规划策略等。1.不确定性的来源在路径规划中，不确定性主要来源于以下几个方面：1.1传感器误差传感器是路径
  • LeetCode：455.分发饼干 xiaoshiguang3 代码随想录-跟着Carl学算法leetcode算法java
    跟着carl学算法，本系列博客仅做个人记录，建议大家都去看carl本人的博客，写的真的很好的！代码随想录假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子i，都有一个胃口值g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干j，都有一个尺寸s[j]。如果s[j]>=g[i]，我们可以将这个饼干j分配给孩子i，这个孩子会得到满足。你的目标是满足
  • day_03_查找算法、排序算法 幻影maple 数据结构与算法查找算法排序算法
    六算法的概念和评价1基本概念2评定标准3描述方式七常用的查找算法1线性查找算法顺序查找算法1算法流程2算法评价2二分查找算法折半查找算法1算法流程2算法评价八常用的排序算法1冒泡排序算法1算法流程2算法评价2插入排序算法1算法流程2算法评价3选择排序算法1算法流程2算法评价4快速排序算法1算法流程2算法评价六、算法的概念和评价1、基本概念算法就是指对解题方案准确而又完整的描述，是一系列解决问题的清
  • python实现冒泡排序完整算法_利用python实现冒泡排序算法实例代码 weixin_39610759
    利用python实现冒泡排序算法实例代码冒泡排序冒泡排序（英语：BubbleSort）是一种简单的排序算法。它重复地遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。冒泡排序算法的运作如下：1、比较相邻的元素。如果第一个比第二个大（升序
  • 新星计划Day11【数据结构与算法】 排序算法2 京与旧铺 java学习排序算法java算法
    新星计划Day11【数据结构与算法】排序算法2‍博客主页：京与旧铺的博客主页✨欢迎关注点赞收藏⭐留言✒本文由京与旧铺原创，csdn首发！系列专栏：java学习参考网课：尚硅谷首发时间：2022年5月13日你做三四月的事，八九月就会有答案，一起加油吧如果觉得博主的文章还不错的话，请三连支持一下博主哦最后的话，作者是一个新人，在很多方面还做的不好，欢迎大佬指正，一起学习哦，冲冲冲推荐一款模拟面试、刷题
  • BP神经网络概述及其预测的Python和MATLAB实现 追蜻蜓追累了 神经网络回归算法深度学习机器学习启发式算法lstmgru
    ##一、背景###1.1人工神经网络的起源人工神经网络（ArtificialNeuralNetwork,ANN）受生物神经网络的启发，模拟大脑神经元之间的连接和信息处理方式。尽管早在1943年就有学者如McCulloch和Pitts提出了数学模型，但人工神经网络真正被广泛研究是在20世纪80年代。###1.2BP神经网络的兴起反向传播（BackPropagation，简称BP）算法是20世纪80年
  • 【DAY.2】PHP数据结构与算法_排序_冒泡排序 我是妖怪_ 天天学习冒泡排序算法php
    思路分析：循环逐个对比，从第一个开始，与下一个数字进行对比，若大于则交换位置，每循环一遍将最大的一个排到最后。（依次比较相邻的元素，两两比较，就可以最终将最大（小）的元素调整到最顶端、次顶端、、、）$arr=array(3,2,5,6,1,8,4,9);functionbubble_sort($arr){$len=count($arr);//判断数组是否为空if($len$arr[$i+1]){$
  • python转转商超书籍信息爬虫 Python数据分析与机器学习 爬虫python网络爬虫爬虫
    1基本理论1.1概念体系网络爬虫又称网络蜘蛛、网络蚂蚁、网络机器人等，可以按照我们设置的规则自动化爬取网络上的信息，这些规则被称为爬虫算法。是一种自动化程序，用于从互联网上抓取数据。爬虫通过模拟浏览器的行为，访问网页并提取信息。这些信息可以是结构化的数据（如表格数据），也可以是非结构化的文本。爬虫任务的执行流程通常包括发送HTTP请求、解析HTML文档、提取所需数据等步骤。1.2技术体系1请求库:
  • 机器视觉在医疗影像分析中的应用：助力放射科医生精准诊断 人工智能专属驿站 大数据人工智能计算机视觉
    在现代医疗领域，影像学检查如X光、CT扫描和MRI等是诊断疾病的重要手段。随着技术的不断发展，机器视觉算法在医疗影像分析中的应用日益广泛，为放射科医生提供了强大的辅助工具，极大地提高了诊断的准确性和效率。本文将探讨机器视觉在医疗影像分析中的具体应用及其对医疗诊断带来的变革。一、机器视觉算法简介机器视觉是一种模拟人类视觉的科学技术，通过图像处理、模式识别和计算机视觉等技术，使计算机能够“看”懂图像中
  • Day_1 数据结构与算法&LeetCode入门及攻略 Finger-Von-Frings c++leetcode
    数据结构与算法学习目的：我们学习算法和数据结构，是为了学会在编程中从时间复杂度、空间复杂度方面考虑解决方案，训练自己的逻辑思维，从而写出高质量的代码，以此提升自己的编程技能，获取更高的工作回报。数据结构定义：数据结构(DataStructure)指的是带有结构特性的数据元素的集合。学习的目的：为了帮助我们了解和掌握计算机中的数据是以何种方式进行组织、存储的。Q1：何为结构特性？所谓结构特性，指的是
  • 二分(C++) 数的范围 三次方根 你干码，哎哟 算法c++排序算法
    二分通常指的是二分查找（BinarySearch），它是一种高效的查找算法，用于在有序数组中查找某一特定元素的位置。二分查找的思路是：每次取中间位置的元素与目标值进行比较。如果中间位置的元素正好等于目标值，则查找成功。如果中间位置的元素大于目标值，则在数组的左半部分继续查找。如果中间位置的元素小于目标值，则在数组的右半部分继续查找。重复上述过程，直到找到目标值或查找范围为空。一.数的范围题目给定一
  • 华为OD机试E卷 --数大雁--24年OD统一考试（Java & JS & Python & C & C++） 飞码创造者 最新华为OD机试题库2024华为odjavajavascriptpythonjsc语言
    文章目录题目描述输入描述输出描述用例题目解析JS算法源码Java算法源码python算法源码c算法源码题目描述一群大雁往南飞，给定一个字符串记录地面上的游客听到的大雁叫声，请给出叫声最少由几只大雁发出。具体：1.大雁发出的完整叫声为”quack“，因为有多只大雁同一时间嘎嘎作响，所以字符串中可能会混合多个”quack”2.大雁会依次完整发出”quack”，即字符串中’q，u,a，c，k这5个字母按
  • 程序设计思考：归零思想 hookby 程序设计
    “归零思想”是一种在程序设计中常用的思考方法，主要指的是通过将某些值或状态归零，来简化问题或解决复杂度。这个思想在许多领域中都可以找到应用，尤其是在处理问题时需要清理和重置状态，避免累积错误或多余的计算。下面是几个典型的应用场景：1.状态重置在某些算法中，特别是动态规划、回溯、递归等问题中，我们可能需要在每个阶段重置某些变量或状态，防止它们影响后续的计算。例如，在递归算法中，递归结束后可以通过将某
  • BP神经网络及其Python和MATLAB实现预测 陈辰学长 神经网络pythonmatlab
    BP神经网络及其Python和MATLAB实现预测引言BP神经网络（BackPropagationNeuralNetwork），即反向传播神经网络，是一种通过反向传播算法进行监督学习的多层前馈网络。这种网络能够通过不断地调整和改变神经元的连接权重，达到对特定任务的学习和优化。由于其高度的灵活性和适应性，BP神经网络在模式识别、函数逼近、优化问题等多个领域有着广泛的应用。本文将详细介绍BP神经网络的
  • 保护你的会话令牌 博文视点 信息安全技术ESAPIOWASPTop10webWebWEB会话安全
    保护你的会话令牌通常我们会采取以下的措施来保护会话。1．采用强算法生成SessionID正如我们前面用WebScrab分析的那样，会话ID必须具有随机性和不可预测性。一般来说，会话ID的长度至少为128位。下面我们就拿常见的应用服务器Tomcat来说明如何配置会话ID的长度和生成算法。首先我们找到{TOMCAT_HOME}\conf\context.xml，然后加入下面一段设置➊定义会话ID的长度
  • web报表工具FineReport常见的数据集报错错误代码和解释 老A不折腾 web报表finereport代码可视化工具
    在使用finereport制作报表，若预览发生错误，很多朋友便手忙脚乱不知所措了，其实没什么，只要看懂报错代码和含义，可以很快的排除错误，这里我就分享一下finereport的数据集报错错误代码和解释，如果有说的不准确的地方，也请各位小伙伴纠正一下。   NS-war-remote=错误代码\:1117 压缩部署不支持远程设计 NS_LayerReport_MultiDs=错误代码
  • Java的WeakReference与WeakHashMap bylijinnan java弱引用
    首先看看 WeakReference wiki 上 Weak reference 的一个例子： public class ReferenceTest { public static void main(String[] args) throws InterruptedException { WeakReference r = new Wea
  • Linux——（hostname）主机名与ip的映射 eksliang linuxhostname
    一、 什么是主机名 无论在局域网还是INTERNET上，每台主机都有一个IP地址，是为了区分此台主机和彼台主机，也就是说IP地址就是主机的门牌号。但IP地址不方便记忆，所以又有了域名。域名只是在公网（INtERNET)中存在，每个域名都对应一个IP地址，但一个IP地址可有对应多个域名。域名类型 linuxsir.org 这样的； 主机名是用于什么的呢？ 答：在一个局域网中，每台机器都有一个主
  • oracle 常用技巧 18289753290
    oracle常用技巧 ①复制表结构和数据   create table  temp_clientloginUser as   select distinct userid from tbusrtloginlog ②仅复制数据 如果表结构一样 insert into  mytable  select  * &nb
  • 使用c3p0数据库连接池时出现com.mchange.v2.resourcepool.TimeoutException 酷的飞上天空 exception
    有一个线上环境使用的是c3p0数据库，为外部提供接口服务。最近访问压力增大后台tomcat的日志里面频繁出现 com.mchange.v2.resourcepool.TimeoutException: A client timed out while waiting to acquire a resource from com.mchange.v2.resourcepool.BasicResou
  • IT系统分析师如何学习大数据 蓝儿唯美 大数据
    我是一名从事大数据项目的IT系统分析师。在深入这个项目前需要了解些什么呢？学习大数据的最佳方法就是先从了解信息系统是如何工作着手，尤其是数据库和基础设施。同样在开始前还需要了解大数据工具，如Cloudera、Hadoop、Spark、Hive、Pig、Flume、Sqoop与Mesos。系 统分析师需要明白如何组织、管理和保护数据。在市面上有几十款数据管理产品可以用于管理数据。你的大数据数据库可能
  • spring学习——简介 a-john spring
    Spring是一个开源框架，是为了解决企业应用开发的复杂性而创建的。Spring使用基本的JavaBean来完成以前只能由EJB完成的事情。然而Spring的用途不仅限于服务器端的开发，从简单性，可测试性和松耦合的角度而言，任何Java应用都可以从Spring中受益。其主要特征是依赖注入、AOP、持久化、事务、SpringMVC以及Acegi Security 为了降低Java开发的复杂性，
  • 自定义颜色的xml文件 aijuans xml
    <?xml version="1.0" encoding="utf-8"?> <resources> <color name="white">#FFFFFF</color> <color name="black">#000000</color> &
  • 运营到底是做什么的？ aoyouzi 运营到底是做什么的？
    文章来源：夏叔叔（微信号：woshixiashushu），欢迎大家关注！很久没有动笔写点东西，近些日子，由于爱狗团产品上线，不断面试，经常会被问道一个问题。问：爱狗团的运营主要做什么？答：带着用户一起嗨。为什么是带着用户玩起来呢？究竟什么是运营？运营到底是做什么的？那么，我们先来回答一个更简单的问题——互联网公司对运营考核什么？以爱狗团为例，绝大部分的移动互联网公司，对运营部门的考核分为三块——用
  • js面向对象类和对象 百合不是茶 js面向对象函数创建类和对象
    接触js已经有几个月了,但是对js的面向对象的一些概念根本就是模糊的,js是一种面向对象的语言 但又不像java一样有class,js不是严格的面向对象语言 ,js在java web开发的地位和java不相上下  ,其中web的数据的反馈现在主流的使用json,json的语法和js的类和属性的创建相似   下面介绍一些js的类和对象的创建的技术   一:类和对
  • web.xml之资源管理对象配置 resource-env-ref bijian1013 javaweb.xmlservlet
    resource-env-ref元素来指定对管理对象的servlet引用的声明，该对象与servlet环境中的资源相关联 <resource-env-ref> <resource-env-ref-name>资源名</resource-env-ref-name> <resource-env-ref-type>查找资源时返回的资源类
  • Create a composite component with a custom namespace sunjing
    https://weblogs.java.net/blog/mriem/archive/2013/11/22/jsf-tip-45-create-composite-component-custom-namespace   When you developed a composite component the namespace you would be seeing would
  • 【MongoDB学习笔记十二】Mongo副本集服务器角色之Arbiter bit1129 mongodb
     一、复本集为什么要加入Arbiter这个角色 回答这个问题，要从复本集的存活条件和Aribter服务器的特性两方面来说。 什么是Artiber？ An arbiter does not have a copy of data set and cannot become a primary. Replica sets may have arbiters to add a
  • Javascript开发笔记 白糖_ JavaScript
    获取iframe内的元素 通常我们使用window.frames["frameId"].document.getElementById("divId").innerHTML这样的形式来获取iframe内的元素，这种写法在IE、safari、chrome下都是通过的，唯独在fireforx下不通过。其实jquery的contents方法提供了对if
  • Web浏览器Chrome打开一段时间后，运行alert无效 bozch Webchormealert无效
    今天在开发的时候，突然间发现alert在chrome浏览器就没法弹出了，很是怪异。 试了试其他浏览器，发现都是没有问题的。 开始想以为是chorme浏览器有啥机制导致的，就开始尝试各种代码让alert出来。尝试结果是仍然没有显示出来。 这样开发的结果，如果客户在使用的时候没有提示，那会带来致命的体验。哎，没啥办法了 就关闭浏览器重启。   结果就好了，这也太怪异了。难道是cho
  • 编程之美-高效地安排会议 图着色问题 贪心算法 bylijinnan 编程之美
    import java.util.ArrayList; import java.util.Collections; import java.util.List; import java.util.Random; public class GraphColoringProblem { /**编程之美 高效地安排会议 图着色问题 贪心算法 * 假设要用很多个教室对一组
  • 机器学习相关概念和开发工具 chenbowen00 算法matlab机器学习
    基本概念： 机器学习(Machine Learning, ML)是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。 它是人工智能的核心，是使计算机具有智能的根本途径，其应用遍及人工智能的各个领域，它主要使用归纳、综合而不是演绎。 开发工具 M
  • [宇宙经济学]关于在太空建立永久定居点的可能性 comsci 经济
           大家都知道,地球上的房地产都比较昂贵,而且土地证经常会因为新的政府的意志而变幻文本格式........        所以,在地球议会尚不具有在太空行使法律和权力的力量之前,我们外太阳系统的友好联盟可以考虑在地月系的某些引力平衡点上面,修建规模较大的定居点
  • oracle 11g database control 证书错误 daizj oracle证书错误oracle 11G 安装
    oracle 11g database control 证书错误  win7 安装完oracle11后打开 Database control 后，会打开em管理页面，提示证书错误，点“继续浏览此网站”，还是会继续停留在证书错误页面 解决办法： 是 KB2661254 这个更新补丁引起的，它限制了 RSA 密钥位长度少于 1024 位的证书的使用。具体可以看微软官方公告：
  • Java I/O之用FilenameFilter实现根据文件扩展名删除文件 游其是你 FilenameFilter
    在Java中，你可以通过实现FilenameFilter类并重写accept(File dir, String name) 方法实现文件过滤功能。 在这个例子中，我们向你展示在“c:\\folder”路径下列出所有“.txt”格式的文件并删除。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
  • C语言数组的简单以及一维数组的简单排序算法示例，二维数组简单示例 dcj3sjt126com carray
    # include <stdio.h> int main(void) { int a[5] = {1, 2, 3, 4, 5}; //a 是数组的名字 5是表示数组元素的个数，并且这五个元素分别用a[0], a[1]...a[4] int i; for (i=0; i<5; ++i) printf("%d\n",
  • PRIMARY, INDEX, UNIQUE 这3种是一类 PRIMARY 主键。 就是 唯一 且 不能为空。 INDEX 索引，普通的 UNIQUE 唯一索引 dcj3sjt126com primary
    PRIMARY, INDEX, UNIQUE 这3种是一类PRIMARY 主键。 就是 唯一 且 不能为空。INDEX 索引，普通的UNIQUE 唯一索引。 不允许有重复。FULLTEXT 是全文索引，用于在一篇文章中，检索文本信息的。举个例子来说，比如你在为某商场做一个会员卡的系统。这个系统有一个会员表有下列字段：会员编号   INT会员姓名  
  • java集合辅助类 Collections、Arrays shuizhaosi888 CollectionsArraysHashCode
      Arrays、Collections   1 ）数组集合之间转换 public static <T> List<T> asList(T... a) { return new ArrayList<>(a); }      a）Arrays.asL
  • Spring Security（10）——退出登录logout 234390216 logoutSpring Security退出登录logout-urlLogoutFilter
           要实现退出登录的功能我们需要在http元素下定义logout元素，这样Spring Security将自动为我们添加用于处理退出登录的过滤器LogoutFilter到FilterChain。当我们指定了http元素的auto-config属性为true时logout定义是会自动配置的，此时我们默认退出登录的URL为“/j_spring_secu
  • 透过源码学前端 之 Backbone 三 Model 逐行分析JS源代码 backbone源码分析js学习
    Backbone 分析第三部分  Model 概述： Model 提供了数据存储，将数据以JSON的形式保存在 Model的 attributes里， 但重点功能在于其提供了一套功能强大，使用简单的存、取、删、改数据方法，并在不同的操作里加了相应的监听事件， 如每次修改添加里都会触发 change，这在据模型变动来修改视图时很常用，并且与collection建立了关联。
  • SpringMVC源码总结（七）mvc:annotation-driven中的HttpMessageConverter 乒乓狂魔 springMVC
    这一篇文章主要介绍下HttpMessageConverter整个注册过程包含自定义的HttpMessageConverter，然后对一些HttpMessageConverter进行具体介绍。 HttpMessageConverter接口介绍： public interface HttpMessageConverter<T> { /** * Indicate
  • 分布式基础知识和算法理论 bluky999 算法zookeeper分布式一致性哈希paxos
      分布式基础知识和算法理论 BY [email protected] 本文永久链接：http://nodex.iteye.com/blog/2103218   在大数据的背景下，不管是做存储，做搜索，做数据分析，或者做产品或服务本身，面向互联网和移动互联网用户，已经不可避免地要面对分布式环境。笔者在此收录一些分布式相关的基础知识和算法理论介绍，在完善自我知识体系的同
  • Android Studio的.gitignore以及gitignore无效的解决 bell0901 androidgitignore
    　　github上.gitignore模板合集，里面有各种.gitignore ： https://github.com/github/gitignore 　　自己用的Android Studio下项目的.gitignore文件，对github上的android.gitignore添加了 　　　　　　# OSX files　　　　　　//mac os下　　　　　　.DS_Store
  • 成为高级程序员的10个步骤 tomcat_oracle 编程
    What 软件工程师的职业生涯要历经以下几个阶段：初级、中级，最后才是高级。这篇文章主要是讲如何通过 10 个步骤助你成为一名高级软件工程师。   Why 得到更多的报酬！因为你的薪水会随着你水平的提高而增加 提升你的职业生涯。成为了高级软件工程师之后，就可以朝着架构师、团队负责人、CTO 等职位前进 历经更大的挑战。随着你的成长，各种影响力也会提高。
  • mongdb在linux下的安装 xtuhcy mongodblinux
    一、查询linux版本号： lsb_release -a  LSB Version:    :base-4.0-amd64:base-4.0-noarch:core-4.0-amd64:core-4.0-noarch:graphics-4.0-amd64:graphics-4.0-noarch:printing-4.0-amd64:printing-4.0-noa
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他