python进阶之数据结构与算法--中级-哈希表（小白piao分享）

1、 哈希表的概念

     一种python用来实现map和dict的数据结构，称其为哈希表；众所周知一个映射M使用键k作为索引M[k]。由此哈希表有了更进一步的定义，通过哈希函数将每一个一般的键映射到一个表中的相应索引上。理想状况下，键由哈希函数分配到【0，N-1】的范围上，但实际情况可能有两个乃至于多个键映射到同一个索引上。因此，我们将表的概念定义为桶数组（哈希表底层实现的根本数据结构），该数组内有N个桶，每个桶内有键值对元组（一个或者多个，或者None）。如下图：

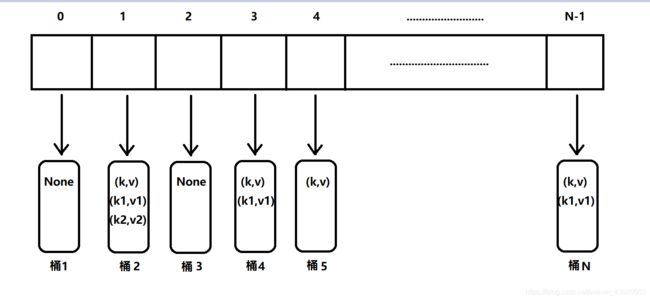
     每个桶都管理一个元组集合，二这些元组则通过哈希函数发送到具体的索引。

2、哈希函数

     哈希函数h的目的非常明确，就是把元组（元组中的两个元素为映射）中的键k映射到【0，N-1】上，N是哈希表桶数组的长度。既有h(k) mod N（mod表示映射关系）；使用这种哈希函数的主要目的是使用哈希函数值h(k)作为哈希桶数组M内部的索引，而不是用键k直接作为桶数组的索引，也就是说，我们用 M[ h( k ) ] 索引桶中元素( k, v )。
     如果有多个元素的键都具有相同的哈希值，那将会导致不同元素被映射到相同桶当中，这就是所谓的冲突，说简单点就是不同键值对拥有相同哈希值会出现问题。当然我们也要尽量降低冲突。而要降低冲突可以从哈希函数的最重要的两个组件入手：哈希码和压缩函数，二者共同完成一个哈希函数。二者也是评价哈希函数的重要指标。

2.1、哈希码

     将一个键映射到一个整数，而这个整数不一定就在【0，N-1】的范围内，甚至有可能为负，而这个整数值，就被称之为这个键的哈希码。
     哈希码的计算独立于具体的哈希表的大小，这样就可以为每个对象开发一个通用的哈希码。并且可以用于任何大小的哈希表。
     将键值映射哈希码也是哈希函数优先处理的一个步骤，其后才会轮到压缩函数。
     如果键的哈希码产生了冲突（一码多键），那压缩函数也无济于事，无法降低该冲突了，所以尤为重要的一点是如何在映射哈希码时将冲突降到最低？这里有几种哈希码实现的理论，后续我们会讨论哈希码生成的具体代码实现。

2.1.1 将位作为整数处理

     这是最直接最容易理解的一种哈希码定义方式，但是同样存在的问题也很多。
     首相，对于任何数据类型X使用尽可能多的位作为它（X本身）的整数哈希码。可以简单地把用于表示整数X（这里暗示了整数键一般可以采用位来生成哈希码）的各个位作为它的哈希码，例如整数键102，就可以用102代表其哈希码。但是有弊端，因为如果是浮点型键，如果浮点数用64位表示那将会无法直接表示（因为哈希码是32位的），一种可能的解决方案是使用低阶32位或者高阶32位表示其哈希码，但是其哈希码将会忽略原键的一半信息，这里有可能会发生冲突，万一两个浮点数的高或低阶相同呢？更好的解决方案是对64位中的高阶和低阶32位求和后者求异或。

2.1.2 多项式哈希码

     以上用求和或者异或的方法对于字符串或一些可变长的对象（元组(x0,x1,x2,x3,x4,…,xn-1)形式表示） 并不是一个好的选择，这里xi的顺序很重要。比如，用一个字符串 'stop’的Unicode码的和 来表示该字符串的哈希码将会带来很多不必要的冲突（‘sotp’，‘spot’，‘post’等字符串的哈希码将会相同）。
     更好的哈希码应该考虑xi位置的问题，这里一种可选的哈希码设计方式可以满足定义要求，选择一个非零常数m，且m不等于1。用如下形式计算哈希码：

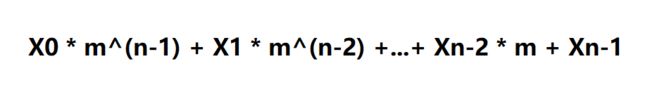
图注：*代表乘，^代表幂（次方）

     这种哈希码的计算方式就是多项式哈希码。从数学角度上来说，这就是一个包含m并且以对象x的元组((x0,x1,x2,x3,…,xn-1))中的元素为系数的一个多项式。该多项式可以用如下方式计算：

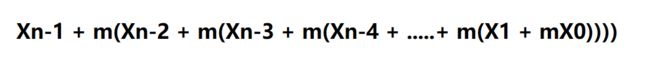
    这种哈希码计算方式的根本就是分散（使每一部分拥有不同的权重）每一部分对哈希码整体的影响。

2.1.3 循环位移哈希码

    一个多项式哈希码的变种，用一定数量的位循环位移得到的部分和 来替代乘以上边提到的常数m。尽管这种操作在算数方面收效甚微，但是其完成了改变二进制位的计算目标。在python中二进制循环移位可以通过>>和<<来完成。从而截取结果为32位整数。经过大量测试结论，我们得出，字符串哈希码计算最优解，结果是在23000个单词中产生了190个冲突的5位移法。python中字符串循环位移的哈希码计算实现如下：

# 字符串5移位法哈希码计算实现：
def hash_str(s):
    mask = (1 << 32) - 1
    hash_c = 0 # 每个字符的哈希码
    for c in s:
        hash_c = (hash_c << 5&mask)|(hash_c >>27)
        hash_c += ord(c)
    return hash_c
# 代码仅供参考。实现源自于网络

2.1.4 python中的哈希码

    python中得到一个对象的哈希码，实际非常方便，python为我们提供了内置函数hash(x)，其返回值为x的哈希码，且该值为整型值。在python中只有不可变对象才是可以哈希的，为什么呢？其实原因很简单，就是因为键在程序运行中不能改变。所以换句话说，能够做键的数据类型才能被哈希 。不可变的数据类型有：**int、float、str、tuple、frozenset。**例如对一个frozenset对象哈希时，由于fronzet本身元素无序，所以一个自然的方法就是直接使用异或（将位按照整型处理2.1.1）计算单个哈希码即可。如果hash中的参数是一个可变对象，会报错TypeError。
    在默认情况下，用户定义的类被视为是不可哈希的，并且hash(x)会直接报错TypeError。如果修改了底层特殊方法__hash__ ，且 其函数内部所有参数均是不可变的类型之后，该类便可以哈希。例如：

def __hash__(self):
	return hash((1,2,3))

    有一个非常重要的原则需要遵守，如果通过eq定义了一个该类的等价类，则__hash__任何实现必须一致，即如果x==y,则hash(x)==hash(y)。这一规则可以扩展到和数据类型的对象间进行比较，例如hash(5) == hash(5.0)，结果返回True。

2.2、压缩函数

    通常键k的哈希码不适宜直接在桶数组中表示桶的索引，因为哈希码的范围未定。我呢决定对一个对象的键k使用整型哈希码时，得进行一步操作，将哈希码映射在【0，N-1】的区间上，这就是压缩函数所做的事情。
    一个好的压缩函数，会使一组哈希码的冲突数量达到最小。

3、冲突解决方案

    哈希表的主要思想是，使用一个哈希桶数组A和一个哈希函数h，并用它们通过对桶M[h(k)]中存储的每个元组进行排序实现映射。但是当有两个不同的对象k1和k2使h(k1) == h(k2)，则会出现冲突。由于存在这样冲突的可能，所以我们不能够简单的直接将新元组(k,v)直接插入到桶M[h(k)]中。
    就此，产生了在插入元组前的冲突解决方案，有如下几种方案：分离链表、开放寻址、线性探测及其变种。

3.1、分离链表

    解决冲突最简单有效的方法是使桶存储自己的二级容器，容器存储元组(k,v)，如h(k)=j,用一个很小的list来实现mao实例是实现二级容器很自然的选择。这种解决方案称之为分离链表。

3.2、开放寻址

    分离链表很简单且容易理解，但是采用链表这种辅助结构（存放冲突元组）在内存开销上是一笔大的支出，且实现也不容易。所以就有了开放寻址的概念，其强调不用辅助结构直接在桶数组本身内将每个元组存储在一个小的列表插槽内，从而达到节省空间的目的。但它需要一个更复杂的机制来处理冲突。

3.3、线性探测及其变种

    使用开放寻址处理冲突的一个简单方法就是线性检测。使用这个方法是，如果将(k,v)插入桶M[i]处，则h(k)=i，但是M[i]已经被占用，那么我们将尝试插入M[(i + 1) mod N]，如果依旧被占用则尝试插入M[(i + 2) mod N]，依次进行直到找到一个空桶存放该元组为止。一旦定位到空桶，即可简单地将元组直接插入其中。当我们试图查找键为k的元组时，必须从M[H(k)]开始向后连续检测，直到找到一个键为k的元组或者发现一个空桶为止。