深度学习实例——Keras实现手写数字识别
引言
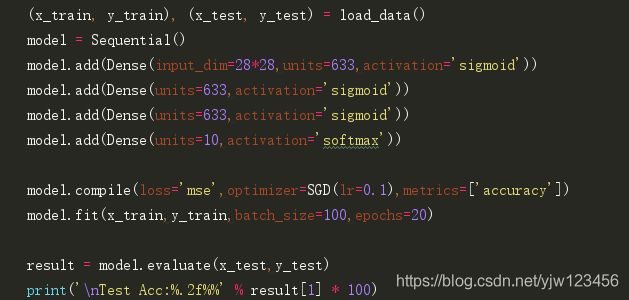
在学习了深度学习的全连接网络后,我们用Keras来实现手写数字识别。使用Keras这种工具的好处是代码非常简短,比如这里可以说是10行代码实现手写数字识别。
但这并不能说明什么,我们需要掌握的是这些代码背后的原理。
(截图最后的print有个问题,把整个字符串输出100次了,后面的代码修复了这个问题)
数据集
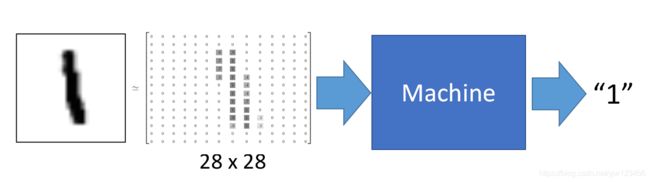
采用的数据集是基本教程都会使用的MNIST数据集。在该数据集中每张图片由28x28个像素点构成,每个像素点用一个灰度值表示。可以将这28x28个像素展开为一个一维的行向量,作为输入,也就是有784x1的向量。
如下是数字1的一个例子,我们的目的是做出一个模型,将这784个数值输入这个模型,然后它的输出是1。
使用Keras
安装
通过pip安装挺简单的,我这里是在Windows10-64环境下:
pip install keras
pip install tensorflow
我用python3.6版本安装tensorflow出现了Could not find a version that satisfies the requirement tensorflow错误,一查发现是python3.6版本不对,我64位电脑安装的是32位的python版本。重新下载一个64位的版本就好了。
下载数据集
接下来就可以下载数据集了,keras中集成了mnist数据集,首先编写如下加载数据集的代码。
from keras.utils import np_utils
from keras.datasets import mnist # keras集成了mnist数据集
def load_data():
(x_train,y_train),(x_test,y_test) = mnist.load_data()
size = 10000 # 测试集大小
x_train = x_train[0:size]# 截取10000个样本
y_train = y_train[0:size]# 截取10000个样本
x_train = x_train.reshape(size,28*28) #x_train本来是10000x28x28的数组,把它转换成10000x784的二维数组
x_test = x_test.reshape(x_test.shape[0],28*28)#和上面是同一个意思
x_train = x_train.astype('float32')#将它的元素类型转换为float32,之前为uint8
x_test = x_test.astype('float32')
# y_train之前可以理解为10000x1的数组,每个单元素数组的值就是样本所表示的数字
y_train = np_utils.to_categorical(y_train,10)# 把它转换成了10000x10的数组
y_test = np_utils.to_categorical(y_test,10)
x_train = x_train/255 # x_train之前的灰度值最大为255,最小为0,这里将它们进行特征归约,变成了在0到1之间的小数
x_test = x_test/255
return (x_train,y_train),(x_test,y_test)
if __name__ == '__main__':
(x_train, y_train), (x_test, y_test) = load_data()
print(x_train.shape) # 10000 x 784
print(y_train[0])
第一次执行的话会先下载数据集:
Using TensorFlow backend.
Downloading data from https://s3.amazonaws.com/img-datasets/mnist.npz
8192/11490434 [..............................] - ETA: 56s
...
11493376/11490434 [==============================] - 28s 2us/step
(10000, 784)
[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] # 这里表示这个样本代表的是数字5
这里x_train是10000x784的数组,代表10000个样本,每个样本有784个维度,每个维度表示一个像素点的灰度值/255;y_train是10000x10的数组,代表着10000个样本的实际输出,这10维度数组中的元素只有1和0,并且只有1个元素是1,其他都是0。元素1所在的索引就代表了实际的数字。比如上面1的索引是5,也就代表该样本的表示的是数字5。
定义函数集
我们知道第一步是定义一个函数集,使用Keras要怎么做呢。
# 定义模型
model = Sequential()
# 定义输入层,全连接网络,输入维度是784,有633个神经元,激活函数是Sigmoid
model.add(Dense(input_dim=28*28,units=633,activation='sigmoid'))
先通过model = Sequential()构造一个模型,然后定义输入维度和输出维度,Dense代表全连接网络,激活函数用的是常见的Sigmoid。
其中激活函数还可以是relu,tanh等等,还可以加入自己自定义的激活函数。
# 定义隐藏层
model.add(Dense(units=633,activation='sigmoid'))
model.add(Dense(units=633,activation='sigmoid'))
接下来通过model.add()来增加一个新的层(这里就是隐藏层了),并指定输出维度是633,它的输入维度就是上一层的输出维度,在隐藏层中不需要指定输入维度,同时别忘了指定激活函数。
# 定义输出层,有10个神经元,也就是10个输出,激活函数是Softmax
model.add(Dense(units=10,activation='softmax'))
最后指定输出层,因为我们要识别数字0~9,共10个,所以指定输出维度为10就好,最后使用的激活函数是softmax。
到此函数集就定义好了。
判断函数的好坏
函数集定义好了,keras如何判断函数的好坏呢。
通过model.compile指定损失函数,这里用的就是均方误差。
model.compile(loss='mse',optimizer=SGD(lr=0.1),metrics=['accuracy'])
选择最好的函数
model.compile中剩下的两个参数是和选择最好的函数相关的。
其中optimizer是和优化学习率有关的,并且有些方法是不需要自己指定初始学习率的,这里用的是SGD(随机梯度下降算法),指定学习率是0.1。
接下来是如何训练了。
model.fit(x_train,y_train,batch_size=100,epochs=20)
x_train是训练集,y_train指定训练集合训练集中每笔数据对应的标签(0~9),每笔数据都是一个numpy数组。
batch_size是批次大小,为什么需要有批次大小呢,因为这里并不是真正的最小化总误差,而是将整个数据集分成固定大小的批次(除了最后一个批次可能数据量不够)。
假设共有10000个数据,我们取100个数据为一个批次,就有100个批次。
-
注意这个划分需要随机,一般划分前先跑一下类似洗牌算法。若没有随机,可能一个批次中全是某个数字,而你总共只训练了2个批次,这样会极大影响最终的准确率。
-
有了批次后,我们随机选一个批次,接着计算该批次中所有数据的总误差,最后更新参数;再选一个批次,计算总误差,更新参数;重复这个步骤…
-
直到选完了所有的批次。
整个过程叫一个迭代(epoch)
所以上面代码说的是批次大小是100,总有20次迭代。
这里不是只更新20次参数,而是更新了20x100=2000次参数。
如果将批次大小设成1,就是随机梯度下降法了。但是一般选用批次大小都不是1。
- 更小的批次大小意味着在一次迭代中更多的更新次数
- 比如,50000个样本
- batch size = 1,1次迭代50000次更新
- batch size = 10,1次迭代5000次更新
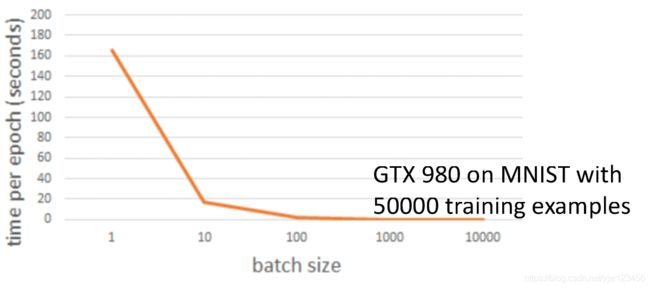
上面是批次大小和每次迭代耗时的关系,可以看到批次大小设成1跑的时间是最长的,随着大小增大,时间是一个递减的关系,直到达到100。
这里我们用了GPU,一次计算10个样本和一次计算1个样本,速度几乎是一样的。但是GPU加速也是有限的,比如这里达到100后,后面在增大批次大小就没有什么意义了。并且批次大小过大还会导致整体运行速度急剧变慢。
测试
测试分为两种情况,一种是用测试集来进行测试,看准确率是多少。
result = model.evaluate(x_test,y_test)
print('\nTest Acc:%.2f%%' % result[1] * 100)
第二种情况就是拿来没有标签的预测真实数据。
result = model.predict(x_test)
完整代码
import numpy as np
from keras.models import Sequential
from keras.layers.core import Dense,Dropout,Activation
from keras.layers import Conv2D,MaxPooling2D,Flatten
from keras.optimizers import SGD,Adam
from keras.utils import np_utils
from keras.datasets import mnist # keras集成了mnist数据集
def load_data():
(x_train,y_train),(x_test,y_test) = mnist.load_data()
size = 10000 # 测试集大小
x_train = x_train[0:size]# 截取10000个样本
y_train = y_train[0:size]# 截取10000个样本
x_train = x_train.reshape(size,28*28) #x_train本来是10000x28x28的数组,把它转换成10000x784的二维数组
x_test = x_test.reshape(x_test.shape[0],28*28)#和上面是同一个意思
x_train = x_train.astype('float32')#将它的元素类型转换为float32,之前为uint8
x_test = x_test.astype('float32')
# y_train之前可以理解为10000x1的数组,每个单元素数组的值就是样本所表示的数字
y_train = np_utils.to_categorical(y_train,10)# 把它转换成了10000x10的数组
y_test = np_utils.to_categorical(y_test,10)
x_train = x_train/255 # x_train之前的灰度值最大为255,最小为0,这里将它们进行特征归一化,变成了在0到1之间的小数
x_test = x_test/255
return (x_train,y_train),(x_test,y_test)
def run():
# 加载数据
(x_train, y_train), (x_test, y_test) = load_data()
# 定义模型
model = Sequential()
# 定义输入层,全连接网络,输入维度是784,有633个神经元,激活函数是Sigmoid
model.add(Dense(input_dim=28*28,units=633,activation='sigmoid'))
# 定义隐藏层
model.add(Dense(units=633,activation='sigmoid'))
model.add(Dense(units=633,activation='sigmoid'))
# 定义输出层,有10个神经元,也就是10个输出,激活函数是Softmax
model.add(Dense(units=10,activation='softmax'))
# 损失函数选择均方误差
model.compile(loss='mse',optimizer=SGD(lr=0.1),metrics=['accuracy'])
model.fit(x_train,y_train,batch_size=100,epochs=20)
result = model.evaluate(x_test,y_test)
print('\nTest Acc:%.2f%%' % (result[1] * 100))
if __name__ == '__main__':
run()
运行结果为:
Test Acc:0.14%
准确率只有14%,这比随机10%的概率好了一点而已。那问题出现在哪里。
Softmax
在机器学习入门之逻辑回归中介绍了这个函数,我们这里回顾一下
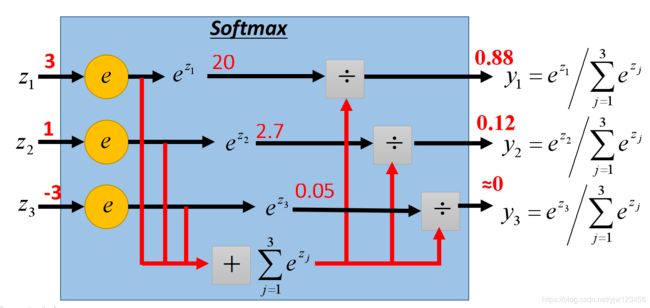
它主要应用在多分类问题,把输入映射为0到1之间的实数,并且归一化保证和为1,因此多分类的概率之和刚好也是1。在我们判断所属类别时,就取概率最大的那个对应的类别。
优化
最终代码能达到准确率96%,本节是探讨如何做的,如果没这耐心的话,可以直接跳到最后的最终代码。
是不是每层633个神经元个数不对,我们把它统一改成28*28:
units = 28*28
# 定义输入层,全连接网络,输入维度是784,有633个神经元,激活函数是Sigmoid
model.add(Dense(input_dim=units,units=units,activation='sigmoid'))
# 定义隐藏层
model.add(Dense(units=units,activation='sigmoid'))
model.add(Dense(units=units,activation='sigmoid'))
# 定义输出层,有10个神经元,也就是10个输出,激活函数是Softmax
model.add(Dense(units=10,activation='softmax'))
再跑:
Test Acc:0.26%
诶,结果真的就好了一点了。肯定还有改进的余地的,是不是我们的层数不够,所谓深度学习,不够深怎么行。然又加上30层隐藏层。
model.add(Dense(input_dim=units,units=units,activation='sigmoid'))
for i in range(30):
# 定义隐藏层
model.add(Dense(units=units,activation='sigmoid'))
#model.add(Dense(units=units, activation='sigmoid'))
#model.add(Dense(units=units,activation='sigmoid'))
# 定义输出层,有10个神经元,也就是10个输出,激活函数是Softmax
model.add(Dense(units=10,activation='softmax'))
再跑(这次比较耗时),结果为:
Test Acc:0.11%
… (结果反而更差了)
上面我们看的都是在测试集上的准确率,我们同时看下在训练集上的准确率,来看是不是根本就没训练起来。
result = model.evaluate(x_train,y_train)
print('\nTrain Acc:%.2f%%' % (result[1] * 100))
(为了速度快一点,先把for训练加30层网络的代码注释起来)
Train Acc:0.11%
可以看到,原来在训练集的准确率也就11%。
这时怎么办呢,其他的都改了,是不是激活函数和误差函数(损失函数)的问题?我们先把误差函数改成交叉熵。
# 损失函数选择交叉熵 keras 中 ategorical_crossentropy表示交叉熵
model.compile(loss='categorical_crossentropy',optimizer=SGD(lr=0.1),metrics=['accuracy'])
model.fit(x_train,y_train,batch_size=100,epochs=20)
输出:
Train Acc:0.84%
真的起来了,在训练集上的准确率立马飙到了84%。接下来看批次大小会不会对结果有影响,我们把它由100改成10000:
model.fit(x_train,y_train,batch_size=10000,epochs=20)
跑的很快,也很快的看到了惨剧:
Train Acc:0.11%
那是不是调太大了,我们改成1,是它变成在线随机梯度算法:
model.fit(x_train,y_train,batch_size=1,epochs=20)
改成1后,就无法发挥GPU的优势了,运算过程变得极慢,而且效果也不好。我也不跑完它了。
接下来,我们再加上30层网络,贴一次完整代码吧:
import numpy as np
from keras.models import Sequential
from keras.layers.core import Dense,Dropout,Activation
from keras.layers import Conv2D,MaxPooling2D,Flatten
from keras.optimizers import SGD,Adam
from keras.utils import np_utils
from keras.datasets import mnist # keras集成了mnist数据集
def load_data():
(x_train,y_train),(x_test,y_test) = mnist.load_data()
size = 10000 # 测试集大小
x_train = x_train[0:size]# 截取10000个样本
y_train = y_train[0:size]# 截取10000个样本
x_train = x_train.reshape(size,28*28) #x_train本来是10000x28x28的数组,把它转换成10000x784的二维数组
x_test = x_test.reshape(x_test.shape[0],28*28)#和上面是同一个意思
x_train = x_train.astype('float32')#将它的元素类型转换为float32,之前为uint8
x_test = x_test.astype('float32')
# y_train之前可以理解为10000x1的数组,每个单元素数组的值就是样本所表示的数字
y_train = np_utils.to_categorical(y_train,10)# 把它转换成了10000x10的数组
y_test = np_utils.to_categorical(y_test,10)
x_train = x_train/255 # x_train之前的灰度值最大为255,最小为0,这里将它们进行特征归一化,变成了在0到1之间的小数
x_test = x_test/255
return (x_train,y_train),(x_test,y_test)
def run():
# 加载数据
(x_train, y_train), (x_test, y_test) = load_data()
# 定义模型
model = Sequential()
units = 28*28
# 定义输入层,全连接网络,输入维度是784,有633个神经元,激活函数是Sigmoid
model.add(Dense(input_dim=units,units=units,activation='sigmoid'))
for i in range(30):
# 定义隐藏层
model.add(Dense(units=units,activation='sigmoid'))
#model.add(Dense(units=units, activation='sigmoid'))
#model.add(Dense(units=units,activation='sigmoid'))
# 定义输出层,有10个神经元,也就是10个输出,激活函数是Softmax
model.add(Dense(units=10,activation='softmax'))
# 损失函数选择交叉熵
model.compile(loss='categorical_crossentropy',optimizer=SGD(lr=0.1),metrics=['accuracy'])
model.fit(x_train,y_train,batch_size=100,epochs=20)
result = model.evaluate(x_train,y_train,batch_size=100) # 这里的批次数量也要加上,不然默认是32
print('\nTrain Acc:%.2f%%' % (result[1] * 100))
result = model.evaluate(x_test,y_test,batch_size=100)
print('\nTest Acc:%.2f%%' % (result[1] * 100))
if __name__ == '__main__':
run()
执行太慢了,我也不等了,第8次迭代后准确率才10%
10000/10000 [==============================] - 17s 2ms/step - loss: 2.3151 - accuracy: 0.1021
Epoch 8/20
在没有30层网络的基础上,我们改了损失函数准确率达到80%多,那接下来我们在改下激活函数试试,把Sigmoid函数改成relu:
units = 28*28
# 定义输入层,全连接网络,输入维度是784,有633个神经元,激活函数是relu
model.add(Dense(input_dim=units,units=units,activation='relu'))
#for i in range(30):
# 定义隐藏层
#model.add(Dense(units=units,activation='relu'))
model.add(Dense(units=units, activation='relu'))
model.add(Dense(units=units,activation='relu'))
# 定义输出层,有10个神经元,也就是10个输出,激活函数是Softmax
model.add(Dense(units=10,activation='softmax'))
在只有2个隐藏层的情况下:
Train Acc:99.98%
Test Acc:95.78%
在训练集上的准确率达到了99.98%,测试集上的准确率也有95.78%。可以看到现在效果是比较能接受的。接下来,加上30个隐藏层,再看下能否做的更好:
for i in range(30):
# 定义隐藏层
model.add(Dense(units=units,activation='relu'))
#model.add(Dense(units=units, activation='relu'))
#model.add(Dense(units=units,activation='relu'))
运算也很近,并且输出不好。看来30层有点多了,我们把它改成10层再试一次:
for i in range(10):
# 定义隐藏层
model.add(Dense(units=units,activation='relu'))
#model.add(Dense(units=units, activation='relu'))
#model.add(Dense(units=units,activation='relu'))
结果:
Train Acc:99.97%
Test Acc:95.77%
结果似乎和2层的差不多。还能调整吗,别忘了,我们还没有调整学习率。可以试试不同的学习率对结果的影响,在这里我就不调了。直接用Adam算法,它能自动调整学习率。
model.compile(loss='categorical_crossentropy',optimizer=Adam(),metrics=['accuracy'])
最终结果:
Train Acc:99.56%
Test Acc:96.02%
在测试集上的准确率达到了96%。
最终代码
from keras.models import Sequential
from keras.layers.core import Dense,Dropout,Activation
from keras.layers import Conv2D,MaxPooling2D,Flatten
from keras.optimizers import SGD,Adam
from keras.utils import np_utils
from keras.datasets import mnist # keras集成了mnist数据集
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 只是防止告警 'I tensorflow/core/platform/cpu_feature_guard.cc:140] Your CPU supports instructions that this',没有真正解决这个问题
def load_data():
(x_train,y_train),(x_test,y_test) = mnist.load_data()
size = 10000 # 测试集大小
x_train = x_train[0:size]# 截取10000个样本
y_train = y_train[0:size]# 截取10000个样本
x_train = x_train.reshape(size,28*28) #x_train本来是10000x28x28的数组,把它转换成10000x784的二维数组
x_test = x_test.reshape(x_test.shape[0],28*28)#和上面是同一个意思
x_train = x_train.astype('float32')#将它的元素类型转换为float32,之前为uint8
x_test = x_test.astype('float32')
# y_train之前可以理解为10000x1的数组,每个单元素数组的值就是样本所表示的数字
y_train = np_utils.to_categorical(y_train,10)# 把它转换成了10000x10的数组
y_test = np_utils.to_categorical(y_test,10)
x_train = x_train/255 # x_train之前的灰度值最大为255,最小为0,这里将它们进行特征归一化,变成了在0到1之间的小数
x_test = x_test/255
return (x_train,y_train),(x_test,y_test)
def run():
# 加载数据
(x_train, y_train), (x_test, y_test) = load_data()
# 定义模型
model = Sequential()
units = 28*28
# 定义输入层,全连接网络,输入维度是784,有633个神经元,激活函数是Sigmoid
model.add(Dense(input_dim=units,units=units,activation='relu'))
for i in range(2):
# 定义隐藏层
model.add(Dense(units=units,activation='relu'))
#model.add(Dense(units=units, activation='relu'))
#model.add(Dense(units=units,activation='relu'))
# 定义输出层,有10个神经元,也就是10个输出,激活函数是Softmax
model.add(Dense(units=10,activation='softmax'))
# 损失函数选择交叉熵
model.compile(loss='categorical_crossentropy',optimizer=Adam(),metrics=['accuracy'])
model.fit(x_train,y_train,batch_size=100,epochs=20)
result = model.evaluate(x_train,y_train,batch_size=100) # 这里的批次数量也要加上,不然默认是32
print('\nTrain Acc:%.2f%%' % (result[1] * 100))
result = model.evaluate(x_test,y_test,batch_size=100)
print('\nTest Acc:%.2f%%' % (result[1] * 100))
if __name__ == '__main__':
run()
运行结果为:
Train Acc:99.56%
Test Acc:96.02%
在测试集上的准确率达到了96%,在训练集上的准确率是99.56%。
在下篇文章中会介绍,我们为什么要进行这样的调整来优化结果。