【深度学习 内力篇】Chap.1 单变量线性回归问题+梯度下降算法+Python建模实战

---

摘要

  我所理解的梯度下降法并不是一个机器学习算法，而是一种基于搜索的最优化方法。梯度下降算法 通过循环计算函数的梯度∇并更新待优化参数值，从而得到函数 获得极小值时参数的最优数值解。梯度下降的中心思想就是迭代的调整参数从而使损失函数最小化。

  值得说明的是，本文 实战篇 并没有使用到任何深度学习框架，只是利用其中的算法逻辑搭建了扼要逻辑框架。
  本文详细说明了梯度下降算法解决单变量线性回归问题的原理，并使用python代码给出了图像可视化证明。其中涉及Python语法方面，我参考《Python编程：从入门到实践》给读者提供了详细注释。

---

2.1 单变量线性回归问题 理论篇

吴恩达机器学习 学习笔记 之 二 ：代价函数和梯度下降算法

---

2.2.1 深度学习在单变量线性回归问题的应用

  在初高中时，为了求解一条线性直线，我们常常采用两点确定一条直线的方法，即知道两个样本即可知道该方程的解析解(Closed-form Solution)。
  但是实际上，对于样本数量大于2个的样本集，这时很有可能不存在解析解，我们只能借助数值方法去优化(Optimize) 出一个近似的数值解(Numerical Solution)。
  为什么叫作优化？这是因为计算机的计算速度非 常快，我们可以借助强大的计算能力去一次次地“搜索”和“试错”，从而一步步降低误差ℒ。
   最简单的优化方法就是暴力搜索或随机试验，比如对于y = w * x + b要找出最合适的w∗和∗，我们就可以从 (部分)实数空间中随机采样任意的和，并计算出对应模型的误差值ℒ（loss），然后从测试过的 {ℒ}中挑出最好的ℒ∗，它所对应的和就可以作为我们要找的最优w∗和∗。
  这种算法固然简单直接，但是面对大规模、高维度数据的优化问题时计算效率极低，基本不可行。
  梯度下降算法(Gradient Descent)是神经网络训练中最常用的优化算法，配合 强大的图形处理芯片GPU(Graphics Processing Unit)的并行加速能力，非常适合优化海量数 据的神经网络模型，自然也适合优化我们这里的神经元线性模型。这里先简单地应用梯度下降算法，用于解决神经元模型预测的问题。
  # 神经元线性模型即单输入单输出的模式的神经元模型，单变量线性模型回归问题可以应用神经网络的逻辑。
  # 需要注意的是，梯度下降法不是一个机器学习算法，而是一种基于搜索的最优化方法。它的作用是最小化一个损失函数从而得到模型参数值。

---

2.1.2 函数模型

目标函数与假设函数
  在机器学习（Machine Learning）中，总是用x来表示输入，y来表示输出；因此，为了研究机器学习就需要一个x与y之间的关系式，我们设为 y=f(x)。
 f(x)称为目标函数(target function) 。
  然而，遗憾的是我们并不知道这样一个关系式。因此，机器学习试图从已知的数据集中预先得知一个函数h(x)；而机器学习的目的就是找到这样一个h(x)，使其近似于（拟合）f(x)。实现推测未知数据的作用。
 h(x)称为假设函数(Hypothesis)。

---

单变量线性回归问题（Linear Regression with one variable）
  就是用一条直线较为精确地描述数据（点集）之间的关系。这样当出现新的数据的时候，就能够预测出一个简单的值。
  例如，房价预测问题：只有房屋面积这一个变量（自变量）影响着价格（因变量）。

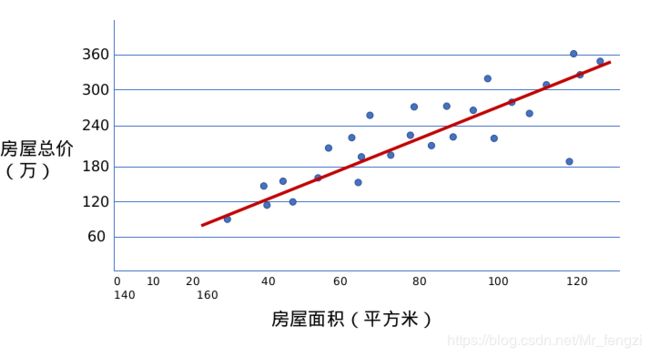
 这条直线的函数模型，用一元一次函数拟合样本数据集，即小学数学的“ y=kx+b ”.

 θ₀ ，θ₁是我们设计模型的关键参数。

---

假设函数 h( x )
  代表学习算法（Learning Algorithm）针对数据集（Training Set）的解决方案或函数也称为假设函数（hypothesis）

 h (x) 是只有一个变量的线性函数。初始作如下定义：

• (x, y) — 一个样本
• (x ⁱ, y ⁱ) — 第i个样本
• x — 输入变量 / 特征（features）
• y — 输出变量 / 目标变量（target varibles）
• m — 训练样本的数量

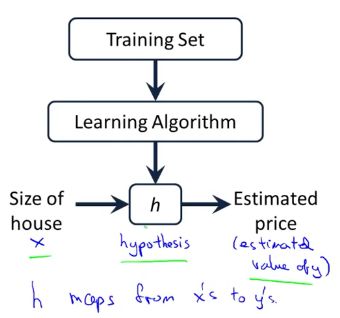
单变量线性回归问题构造函数模型的过程，就是一个有监督学习的工作方式，训练集集中的目标就是通过已有的一部分输入数据与输出数据之间的对应关系，生成一个函数，将输入映射到合适的输出。

我们可以看到这里有我们的训练集里房屋价格 我们把它喂给我们的学习算法，学习算法输出一个函数h(x), h 代表hypothesis(假设)。表示一个函数，输入是房屋尺寸大小， 根据输入的x 值来得出y 值，y 值对应房子的价格, 因此h是一个从x 到 y 的函数映射。

---

我们的目标就是建立这样一个方程。

但是如何评估一个我们所建立这样的方程 ，怎么判断这个函数好不好呢？也就是假设函数h(x) 是否可以用来近似的表示 目标函数f(x) 呢 ?
这个评价标准就是代价函数(cost function)，我们的训练模型的目标就是让代价【cost】最小。（我理解为整体误差）
在线性回归建模问题中，实际上我们要解决的其实是最小化(误差)问题。

---

代价函数(cost function)

  建模得出的参数（parameters）θ₀与θ₁决定了我们得到的直线模型相对于我们的训练集的准确程度。
  这个准确度（误差）的描述也叫代价函数，或是损失函数

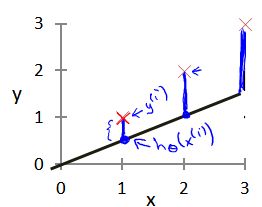
• 单个样本的误差即，模型所预测的值与训练集中实际值之间的差距
  （下图中单条蓝线所指）就是建模误差（modeling error）。
  

• 对于单个样本的误差来说，h (x)-f (x) 的值有正有负，为了统一这种关系以便于平均运算，我们将 ( h (x_i) - f (x_i) )² 视为单个样本的误差。

• 对于整体样本的误差来说，关于训练集的平均损失称作经验风险(empirical risk) 代价函数，是衡量一个假设函数的“损失”，又称作“平方和误差函数”（Square Error Function） ，
  

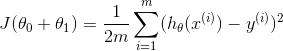
• 同样地，如果我们用均方误差来表达

---

均方误差（mean-square error, MSE）

  均方误差是反映估计量与被估计量之间差异程度的一种度量，换句话说，参数估计值与参数真值之差的平方的期望值。MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。

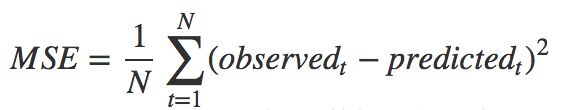
 某些教程此处歧义引用“均方差”，应当是平方差平均损失值，即均方差并不是均方误差

方差、协方差、标准差、均方差、均方根值、均方误差、均方根误差对比分析
均方误差(MSE)和均方根误差(RMSE)和平均绝对误差(MAE)

• 2 x 平方和误差 = 均方误差
  因为后面应用梯度下降算法会求偏导数（带2次幂），所以为了简化运算，我们一般使用平方和误差表达代价函数。

---

  优化的目标
   找到合适地θ₀与θ₁使得代价函数最小。
  如何优化？
   使用梯度下降算法

---

2.2.3 梯度下降算法(Gradient Descent)

1.大白话讲解梯度下降算法
2.图解梯度下降算法
3.梯度下降概念及推导过程

---

梯度
1.梯度与导数的关系

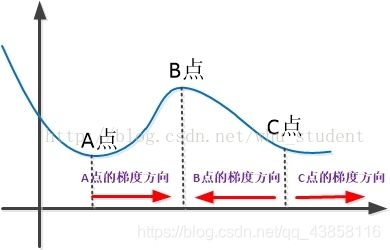
  梯度是矢量而某点的导数是个常量，两者应该有本质的区别，而导数的正负也反映了函数值的大小变化，而不是一直指向数值增大的方向。

2.对梯度的直观理解

  函数的梯度(Gradient)，记做grad，定义为函数对各个自变量的偏导数(Partial Derivative)组成的向量。则梯度∇为向量( / , / )。
梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该此梯度的方向变化最快，变化率最大（为该梯度的模）。

---

梯度下降算法
  梯度下降算法 通过循环计算函数的梯度∇并更新待优化参数值，从而得到函数 获得极小值时参数的最优数值解。梯度下降的中心思想就是迭代的调整参数从而使损失函数最小化。
  需要注意的是，梯度下降法不是一个机器学习算法，而是一种基于搜索的最优化方法。它的作用是最小化一个损失函数从而得到模型参数值。

线性回归中使用梯度下降法的目标：

• 使得均方差误差尽可能得小
  
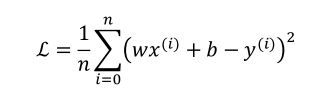
• 需要优化的模型参数是和【θ₀和θ₁】，因此我们按照
  
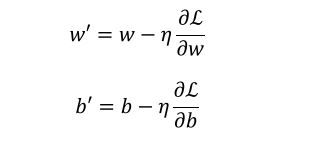
  的方式循环优化参数。
   η是超参数的学习率，其决定了选取的步长。如果学习率太低，算法需要经过大量迭代才能收敛，这将耗费很长时间；如果学习率太高，那你可能会越过谷底直接到达另一边，甚至有可能比之前的起点还高。这会导致算法发散，值越来越大，最后无法找到好的解决方案。

---

循环优化参数

  通过上式方式优化参数的方法称为梯度下降算法 ，其中的 η 指的是学习率

---

梯度下降的局部最小值问题

• 对于MSE来说，因为损失函数是个凸函数，所以不存在局部最小值，只有一个全局最小值
• 通过随机初始化θ，可以避开局部最小值
• 对于多变量，高维度的值，就算在某个维度上陷入和局部最小值，但是还能从别的维度跳出

---

2.2 单变量线性回归问题 实战篇：直线方程的拟合

  为了演视线性回归的准确性，我们需要一条直线的标准方程作为参考：设y = w*x + b。假设，对于已知真实样例中，我们直接从指定的 = 1.447 , = 0.089 的真实模型中直接采样得： = 1.447 ∗ x +0.089。
（1）为了模拟真实的数据，我们随机生成这条直线周围的点作为样本集。
（2）运用梯度下降算法进行拟合曲线，与标准方程作比较。
（3）以均方误差（mean-square error, MSE）作为损失函数，MSE越小，线性拟合越好。并绘图。

---

2.1.1采样数据

制造 “ 困难 ”
制造概率分布的标准差为0.5的高斯噪音，对应于分布的宽度0.5的正态分布曲线

data = []    # 保存样本集的列表
for i in range(100):     # 循环采样 100 个点
    x = np.random.uniform(-10., 10.,1)    # 随机采样输入 x 
    eps = np.random.normal(0., 0.5, size=None)   # 采样高斯噪声 
    y = 1.477 * x + 0.089 + eps    #得到模型的输出
    data.append([x, y])    # 保存样本点
data = np.array(data)    # 转换为 2维 Numpy 数组

代码详解：
  使用函数range()让Python遍历1 ~ 100的值，在每一次游历时描绘一个点，横坐标x是在-10.0 ~ 10.0之间随机的，纵坐标y是手动制造误差之后的样本点，误差值是标准解析值加上采样的高斯噪音。根据真实模型生成的数 据，并保存为Numpy 2维数组。

---

第2行——Python函数range()让你能够轻松地生成一个系列的数字
如果使用range(1,100)输出99个值（1 ~ 99）而不是100个（1 ~ 100）
for in循环使得Python按照range产生的数字顺序开始游历

---

第3行——uniform() 方法将随机生成一个实数，它在 [-10, 10] 范围内。

---

第4行——numpy.random.normal(loc=0.0, scale=0.5, size=None)
生成高斯分布的概率密度随机数
高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。

loc：float
此概率分布的均值（对应着整个分布的中心centre）
scale：float
此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高）
size：int or tuple of ints
输出的shape，默认为None，只输出一个值

---

第6行——append将元素添加到已有list的末尾，多用在for in循环

---

第7行——numpy.array

为什么要用numpy
Python中提供了list容器，可以当作数组使用。但列表中的元素可以是任何对象，因此列表中保存的是对象的指针，这样一来，为了保存一个简单的列表[1,2,3]。就需要三个指针和三个整数对象。对于数值运算来说，这种结构显然不够高效。
Python虽然也提供了array模块，但其只支持一维数组，不支持多维数组(在TensorFlow里面偏向于矩阵理解)，也没有各种运算函数。因而不适合数值运算。
NumPy的出现弥补了这些不足。
（——摘自张若愚的《Python科学计算》）

---

VScode绘图

# -*- coding: utf-8 -*-
# %matplotlib inline  ,如果用Notebook,需要加魔法
import numpy as np 
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
#防止Matplotlib下出现乱码解决办法-先把需要的字体（在系统盘C盘的windows下的fonts目录内）添加到FontProperties中，再调用即可

#1采样数据
data = []#保存样本集的列表
for i in range(100):#循环采样100个点
    x = np.random.uniform(-10,10,1)#随机采样输入X
    # 采样高斯噪声
    eps = np.random.normal(0.,0.5, size=None)
    #得到模型的输出
    y = 1.477*x +0.089 +eps
    data.append([x,y])#保存样本点
data = np.array(data)#转换为2维数组
#print(data)

font = FontProperties(fname=r"C:\Windows\Fonts\simhei.ttf", size=14)  
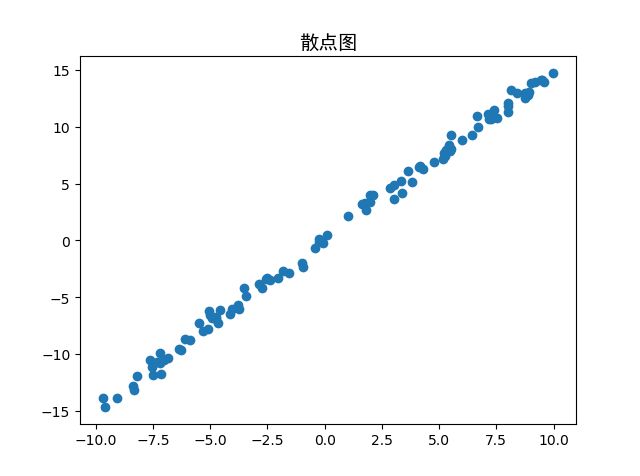
plt.title(u'散点图', FontProperties=font)
plt.scatter(data[:,0], data[:,1])
plt.show()

运行（采样）结果：

---

2.1.2 计算损失函数——（均方）误差

  循环计算在每个点((), ())处的预测值与真实值之间差的平方并累加，从而获得训练集上的均方差损失值（均方误差）。

def mse(b, w, points):   # 根据当前的 w,b 参数计算均方差损失
	totalError = 0       #均方差损失值
	for i in range(len(points)):    # 循环迭代所有点
	    x = points[i, 0]     # 获得i号点的输入x 
	    y = points[i, 1]     # 获得i号点的输出y 
	    totalError += (y - (w * x + b)) ** 2    # 计算各点误差的平方，并累加
        # 将累加的误差求平均，得到均方误差
    return totalError / float(len(points))
    # 最后的误差和除以数据样本总数，从而得到每个样本上的平均误差。

代码详解：

---

第1行——python定义函数的方法【关键字def】。函数能够提高代码的复用性，让代码更简洁。
变量b,w,points是形参,调用函数时加上实参：mse(b, w, data)

---

第3行——Python len() 方法返回对象（字符、列表、元组等）长度或项目个数。这里指的是所采取的样本点的数量。即100个

---

第6行(w * x + b)代表着该函数于该x点的解析值y
python里面**代表数值的平方运算

---

---

2.1.3 计算梯度

代码：计算b、w的梯度：

def step_gradient(b_current, w_current, points, lr): 
    # 计算误差函数在所有点上的导数，并更新 
    w,b b_gradient = 0 
    w_gradient = 0
    M = float(len(points)) # 总样本数
    for i in range(0, len(points)): 
        x = points[i, 0] 
        y = points[i, 1] 
        # 误差函数对 b 的导数：grad_b = 2(wx+b-y)，参考公式(2.3)
        b_gradient += (2/M) * ((w_current * x + b_current) - y)
        # 误差函数对 w 的导数：grad_w = 2(wx+b-y)*x，参考公式(2.2) 
        w_gradient += (2/M) * x * ((w_current * x + b_current) - y)
    # 根据梯度下降算法更新 w',b',其中 lr 为学习率
    new_b = b_current - (lr * b_gradient) 
    new_w = w_current - (lr * w_gradient)
    return [new_b, new_w]

代码解释：不用背公式
具体数学的推到见：梯度下降概念及推导过程
即我们只需要计算在每一个点上面的：(() + − ()) ∙ ()和(() + − ())值，平均后即可得到偏导数（∂ℒ / ∂）和（∂ℒ / ∂）。

---

2.1.4 梯度更新

def gradient_descent(points, starting_b, starting_w, lr, num_iterations):
    #循环更新 w,b 多次 
    b = starting_b # b的初始值 
    w = starting_w # w的初始值
    #根据梯度下降算法更新多次
    for step in range(num_iterations): 
    #计算梯度并更新一次
        b, w = step_gradient(b, w, np.array(points), lr) 
        loss = mse(b, w, points) # 计算当前的均方差，用于监控训练进度 
        if step%50 == 0: # 打印误差和实时的 w,b 值
            print(f"iteration:{step}, loss:{loss}, w:{w}, b:{b}")
return [b, w] # 返回最后一次的 w,b

主训练函数如下：

def main():
    #加载训练集数据，这些数据是通过真实模型添加观测误差采样得到的
    lr = 0.01 # 学习率 
    initial_b = 0 # 初始化 b 为 0
    initial_w = 0 # 初始化 w 为 0 
    num_iterations = 1000 # 训练优化 1000 次，返回最优 w*,b*和训练 Loss 的下降过程
    [b, w], losses = gradient_descent(data, initial_b, initial_w, lr, num_iterations) 
    loss = mse(b, w, data) # 计算最优数值解 w,b 上的均方差
    print(f'Final loss:{loss}, w:{w}, b:{b}')

if __name__ == '__main__':
    main()

代码详解：
if name == ‘main’ 如何正确理解?

---

2.1.5 算法测试+整体源码

整体代码：

# -*- coding: utf-8 -*-

import numpy as np 
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

#1采样数据
data = []
for i in range(100):
    x = np.random.uniform(-10,10,1)
    eps = np.random.normal(0.,0.5, size=None)
    y = 1.477*x +0.089 +eps
    data.append([x,y])
data = np.array(data)

#2计算误差
def mse(b,w,points):
    totalError = 0
    for i in range(0,len(points)):
        x = points[i,0]
        y = points[i,1]
        totalError+=(y-(w*x+b))**2
    return totalError/float(len(points))

#3，计算梯度
def step_gradient(b_current,w_current,points,lr):
    b_gradient = 0
    w_gradient =0
    M = float(len(points))
    for i in range(0,len(points)):
        x = points[i,0]
        y=points[i,1]
        b_gradient +=(2/M)*((w_current*x+b_current)-y)
        w_gradient += (2/M) * x*((w_current*x+b_current) - y)
    new_b = b_current -(lr*b_gradient)
    new_w = w_current -(lr * w_gradient)
    return [new_b,new_w]

#梯度更新
def gradient_descent(points,starting_b,starting_w,lr,num_iterations):
    b = starting_b
    w = starting_w
    loss_data = []
    for step in range(num_iterations):
        b, w = step_gradient(b,w,np.array(points),lr)
        loss = mse(b,w,points)
        loss_data.append([step+1, loss])
        if step % 50 == 0:
            print("iteration:{},loss:{},w:{},b:{}".format(step,loss,w,b))
    return [b, w, loss_data]

def main():
    lr = 0.01
    initial_b = 0
    initial_w = 0
    num_iterations = 1000
    [b, w, loss_data] = gradient_descent(data,initial_b,initial_w,lr,num_iterations)
    loss = mse(b,w,data)
    print("final loss:{},w:{},b:{}".format(loss,w,b))
    font = FontProperties(fname=r"C:\Windows\Fonts\simhei.ttf", size=14)  

    plt.figure()            #观察loss每一步情况
    loss_data = np.array(loss_data)
    plt.plot(loss_data[:,0], loss_data[:,1], 'g')
    plt.savefig('loss.png')
    #plt.show()

    plt.figure()        #观察最终的拟合效果
    plt.scatter(data[:,0], data[:,1], label='Training Set')
    m = np.linspace(-10, 10, +10)
    n = w*m+b
    plt.title(u'单变量线性回归问题', FontProperties=font)
    plt.plot(m,n, label='target function')
    t = 1.477*m+0.089
    plt.plot(m,t, label='Hypothesis')
    plt.legend()
    plt.savefig('final data.png')
    #plt.show()

if __name__ == '__main__':
    main()

---

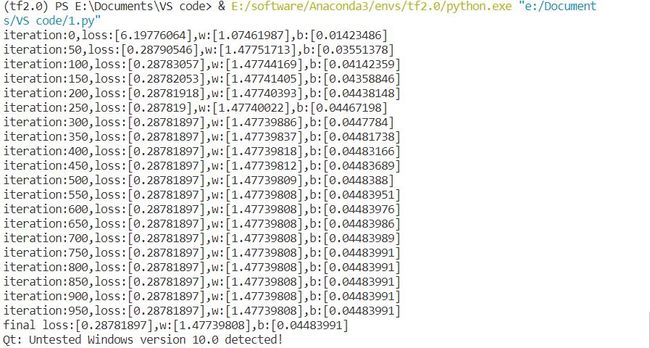
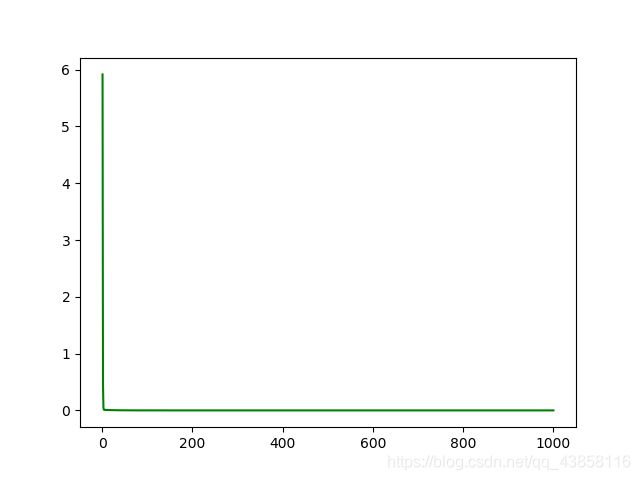
2.1.6 运行结果+代码可视化

• final data.png
  
• 放大一点来看
  
• 训练的次数对应的loss,w,b
  
• loss.png
  

---

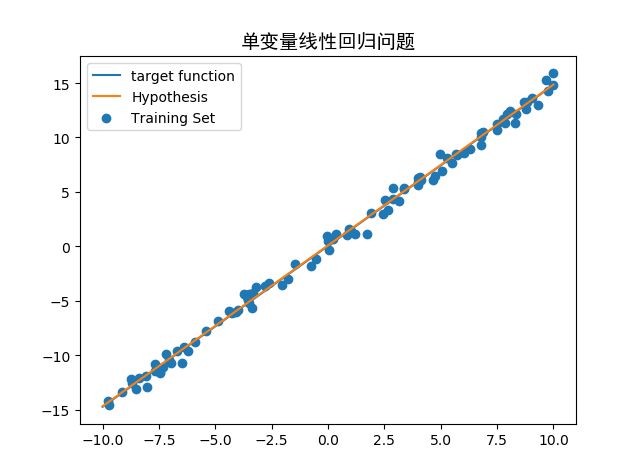
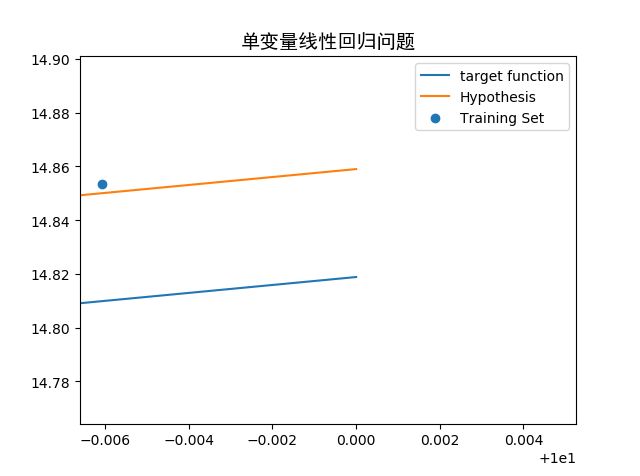
2.1.7 实验结论

  假设函数（Hypothesi）与目标函数（target function）拟合地非常好，误差平均在0.04上，而我们手工给定采样数据的误差【制造概率分布的标准差为0.5的高斯噪音，对应于分布的宽度0.5的正态分布曲线】，说明梯度下降算法可以很好的解决单变量线性回归问题。

相关链接

1. 目标函数、代价函数、结构损失

2. 有监督机器学习、无监督机器学习和半监督学习
   博客链接1
   博客链接2

3. dragen1860 / Deep-Learning-with-TensorFlow-book

4. 吴恩达深度学习课程

5. tensorflow2.0入门与实战 2019年最通俗易懂的课程
   

6. Python编程：从入门到实践：鸠摩、下载

总结

  我选择《吴恩达机器学习课程》课程视频，配合最近GitHub上热门的龙龙老师的书籍《TensorFlow2.0深度学习算法》以及日月光华老师的网课《Tensorflow深度学习入门与实战》，作为我在深度学习入门。Python语法方面我利用《Python编程：从入门到实践》进行同步学习。
  深度学习的核心是算法的设计思想，深度学习框架只是我们实现算法的工具。
  在数学推导方面，吴恩达机器学习课程非常有魅力。并且TensorFlow 2.0 弥补 了 TensorFlow 1.x 在上手难度方面的不足。所以我选择TensorFlow 2.0 版本作为主要框架，实战各种深度 学习算法。
  下一篇我将配合TensorFlow2.0深度学习框架使用单输入神经元线性模型求解单变量线性回归问题。