【深度学习 功法篇】Chap.1 从感知机到人工神经网络（ANN）

---

  本文详细的介绍了由生物学启发的人工神经网络思想，作为深度学习的入门材料，本专栏【深度学习 理论篇】中使用Python 3，尽量不依赖外部库或工具，带领读者从零创建一个经典的深度学习网络，使读者在此过程中逐步理解深度学习。

---

1. MCP神经元——最简单的脑神经元的抽象模型

如何让 机器 像 人类 一样思考 / 学习 ？
人类为什么可以思考 ？
人类是怎样学习的 ？

---

1.1 大脑的神经系统

人类的意识来自于大脑的神经系统，人脑有数十亿个神经（单）元。

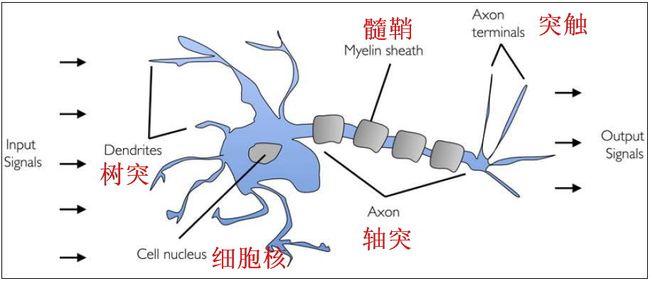
  1943年，研究员Warren McCullock和Walter Pitts提出了第一个脑神经元的抽象模型，简称麦卡洛可-皮茨神经元（McCullock-Pitts neuron）简称MCP神经元。见下图描述：

让我们复习一下高中生物知识：

• 神经元即神经细胞，是神经系统最基本的结构和功能单位。分为细胞体和突起两部分。突起有轴突和树突两种。
• 细胞体由细胞核、细胞膜、细胞质组成，具有联络和整合输入信息并传出信息的作用。
• 树突，短而(分枝)多，直接由细胞体扩张突出，形成树枝状，其作用是接受其他神经元轴突传来的冲动并传给细胞体。接收输入的信息
• 轴突，神经元的输出通道
• 突触，利用递质传递神经冲动，两个神经元之间或神经元与效应器细胞之间相互接触、并借以传递信息的部位。
• 髓鞘，髓鞘是包裹在神经细胞轴突外面的一层膜，即髓鞘由施旺细胞和髓鞘细胞膜组成。其作用是：绝缘，防止神经电冲动从神经元轴突传递至另一神经元轴突。

  神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统，通俗的讲就是具备学习功能。

---

1.2. 人工神经元（The Artificial Neuron）与 感知器（perceptron）

  1957年，Frank Rosenblatt基于MCP神经元 提出了 第一个感知器学习算法，它被描述成最简单的前向传播神经网络 。

---

模仿MCU神经元，搭建一个基本的人工神经元。图解信号传递：
人工记忆神经元是对生物神经元的一种形式化描述，它对生物神经元的信息处理过程进行抽象，并用数学语言予以描述；对生物神经元的结构和功能进行模拟，并用模型图予以表达。

我们提取一个神经元作为研究对象，构造并命名为单层感知机（Single layer perceptrons ），信号传递的过程至关重要。

感知机有四个部分：

1. Input values or One input layer   # 输入&输出
2. Weights and Bias      # 权重&偏置
3. Weighted Sum        # 加权求和
4. Activation Function     # 激活函数

单个神经细胞可被视为一种只有两种状态的机器——激活时为‘是’，而未激活时为‘否’。

感知器的语言描述：
  神经细胞的状态 取决于 从其它的神经细胞收到的输入信号量，及突触的强度（抑制或加强）。当信号量总和超过了某个阈值时，细胞体就会激动，产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。

感知机的概念	模拟神经细胞行为
权量	突触
偏置	偏置
激活函数	细胞体
输出量	轴突

  多个信号到达树突，然后整合到细胞体中，如果累积的信号超过某个阈值，则会生成输出信号，该信号将被轴突传递。

---

2. 单层感知器算法

信号传递的过程是如何在人工神经网络里实现的呢?

---

2.1 单层感知器算法的数学表达

如何让单层感知机可以做出 “是” / “否” 判断呢？
关键的阙值怎样可以用数学语言描述呢？
感知器可不可以实现基本的逻辑呢？

---

  假设感知机接收2个输入信号x1、x2，以及一个用于判断的阙值 b，输出一个信号 y，这个输出的信号只有“0”和“1”两种取值。
可以实现 单层二进制线性分类器 的 监督学习 的算法。

  输入信号x1 和 x2 乘以对应的权重（weight）w1 和 w2，神经元会计算传送过来的信号的总和，如果输入信号的总和超过某个阈值θ,(即下式的 -b )，则输出信号y = 1；否则，输出为y = 0。这也称为“神经元被激活” 。

• 权重越大，对应该权重的信号的重要性就越高。权重用于控制信号流动难度，
• b,偏置（bias），用于调整模型的阙值标准。

用数学式表示：y = h( ) 【激活函数】

激活函数

1. 激活函数的 作用在于决定如何来激活输入信号的总和
2. 信号的加权总和为节点a，然后节点a被激活函数h (x) 转换成节点y

具体步骤：可以分成下面两个式子。

1. a = b + w1x1 + w2x2
2. y = h(a) # 用h()函数将a转换为输出y。

选择合适的激活函数也十分重要

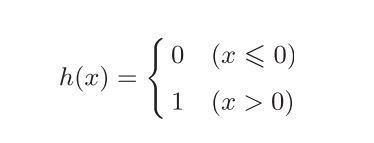
   该式的激活函数以阈值为界，一旦输入超过阈值，就切换输出。 这样的函数称为“阶跃函数”。因此，可以说感知机中使用了阶跃函数作为 激活函数。也就是说，在激活函数的众多候选函数中，下面的感知机使用了阶跃函数。

激活函数

---

2.2 python绘图可视化表达实现简单数字逻辑设计，如与门、非门、或门、异或门等

0和1——最简单的逻辑

• 用0和1可以表示对立的两种逻辑状态：“是”、“否”；
• 与、或、非 是逻辑运算的三种基本运算，其他的逻辑运算可以由这三种基本运算构成。数字逻辑是计算机的基础。

---

例，与门（AND）真值表
【下表的x1、x2代指门电路的两个输入，并不是上文所提输入信号】

用可视化的方式表达：
  在y = x + 0.5 直线之上方的点（1，1）可视为"1"；点（0，0）、（1，0）、（0，1）可视为“0”

import numpy as np
import matplotlib.pyplot as plt
 
x = np.linspace(-3,5, 100)
y = -x + 1.5
plt.xlim(-1,2)
plt.ylim(-1,2)

plt.scatter(0, 0,c='blue')
plt.scatter(0, 1,c='blue')
plt.scatter(1, 0,c='blue')
plt.scatter(1, 1,c='blue')

plt.plot(x, y)
 
plt.title('Linear classifier')
plt.xlabel('x')
plt.ylabel('y')
 
plt.show()

同理可表示NAND,OR等。

---

怎样用程序来描述人类数字逻辑思考的过程？

---

对于 “ 与 ” 运算，AND。
观察下列程序

import numpy as np

def AND(x1, y):
    x = np.array([x1, y])
    w = np.array([1, 1]) # Weight
    b = 1.5 # bias
    tmp = -1 * np.sum(w * x) + b
    if tmp >= 0:
        return 0
    else:
        return 1
        
if __name__ == '__main__':
    for xs in [(0, 0), (0, 1), (1,0),(1, 1)]:
        y = AND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

同样地，我们可以实现与非门、或门的手工搭建。

---

Single layer perceptrons are only capable of learning linearly separable patterns. For a classification task with some step activation function a single node will have a single line dividing the data points forming the patterns.
单层感知器仅能够学习线性可分离模式。 对于具有某些步骤激活功能的分类任务，单个节点将具有一条线，该线将形成模式的数据点分开。

---

  单层感知机只能实现与门、与非门、或门，而不能实现异或门（XOR gate）

---

启发

在这里，确定感知机参数的是人（我），而不是计算机。

  我设计程序的思路是，看着真值表的表现形式确定了模型的参数（w1, w2, b ）分别是（1.0, 1.0, 1.5 ）。所组成的直线：y = -x + 1.5把二维空间里面四个点(0，0)、(0，1)、(1，0) & (1，1)分割成两部分0 & 1。这样可以把输入的x1、x2归类到输出为0或者1上。

  机器学习的课题就是将这个决定参数值的工作交由计算机自动进行。学习是确定合适的参数的过程，而人要做的是思考感知机的构造（模型）【比如这样一个神经网络】，并把训练数据交给计算机。

---

2.4 异或门：单层感知机的局限性

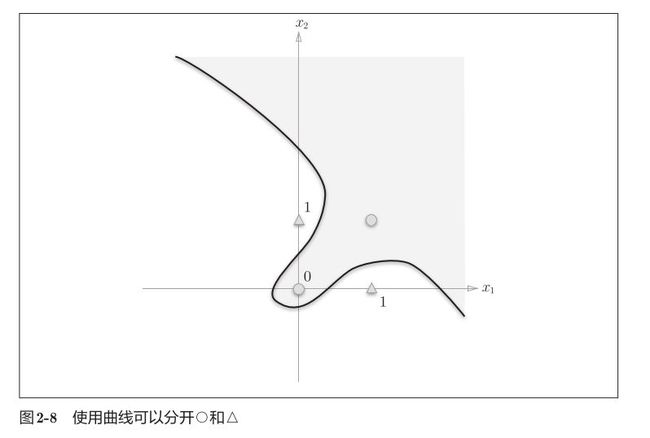
  单层感知机的局限性就在于它只能表示由一条直线分割的空间

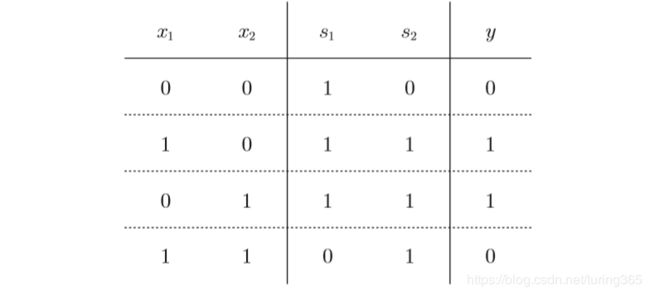
异或门的真值表：仅当x1 或x2 中的一方为1时，才会输出1。

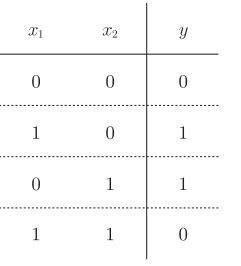
如何才能实现异或门逻辑呢？
即把（0，0）、（1，1）与（0，1）、（1，0）分开呢？

---

3. 多层感知机

多层感知器（Multilayer Perceptron,缩写MLP）是一种前向结构的人工神经网络，映射一组输入向量到一组输出向量。
MLP可以被看作是一个有向图，由多个的节点层所组成，每一层都全连接到下一层。除了输入节点，每个节点都是一个带有非线性激活函数的神经元（或称处理单元）。一种被称为反向传播算法的监督学习方法常被用来训练MLP。
MLP是感知器的推广，克服了感知器不能对线性不可分数据进行识别的弱点。

---

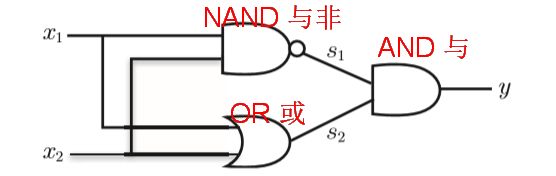
3.1 已有门电路的叠加实现异或逻辑

---

3.2 两层感知机可实现异或门

叠加层手段

---

与“与”门或“与”门不同，“异或”门需要一个中间的隐藏层进行初步转换，以实现“异或”门的逻辑。

• XOR门分配权重，以便满足XOR条件。
• 它不能用单层感知器实现，而需要多层感知器或MLP。
• H代表隐藏层，允许XOR实现。

import numpy as np
def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([1, 1]) # Weight
    b = 1.5 # bias
    tmp = -1 * np.sum(w * x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([1, 1]) # Weight
    b = 0.5 # bias
    tmp = -1 * np.sum(w * x) + b
    if tmp >= 0:
        return 0
    else:
        return 1
        
def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([1, 1]) # Weight
    b = 1.5 # bias
    tmp = -1 * np.sum(w * x) + b
    if tmp >= 0:
        return 0
    else:
        return 1

def XOR(x1,x2):
    s1=NAND(x1,x2)
    s2=OR(x1,x2)
    y=AND(s1,s2)
    return y

if __name__ == '__main__':
    for xs in [(0, 0), (0, 1), (1,0),(1, 1)]:
        y = XOR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

输出结果：

(0, 0) -> 0
(0, 1) -> 1
(1, 0) -> 1
(1, 1) -> 0

---

3.3 多层感知机（multi-layered perceptron）

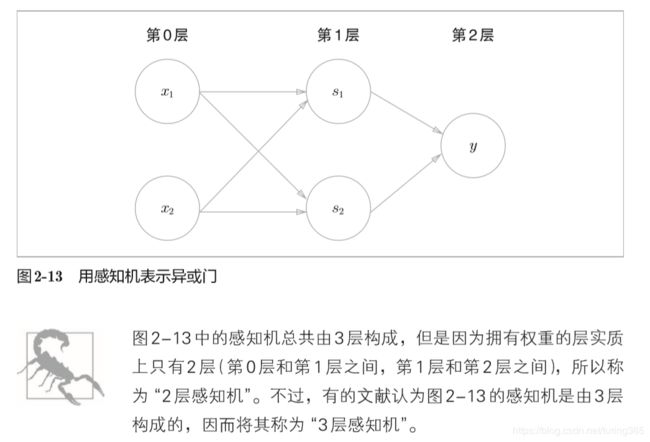
  感知机通过叠加层能够进行非线性的表示，理论上还可以表示一台计算机进行的处理。因为门电路和数字逻辑是现代计算机的基础。

  具有两层或多层的多层感知器或前馈神经网络具有更大的处理能力，并且还可以处理非线性模式。

---

3.4 神经网络——层的叠加到网络模型

• 神经网络由大量的人工神经元联结进行计算。
• 人工神经网络它是一种模仿动物神经网络行为特征，进行‘分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。

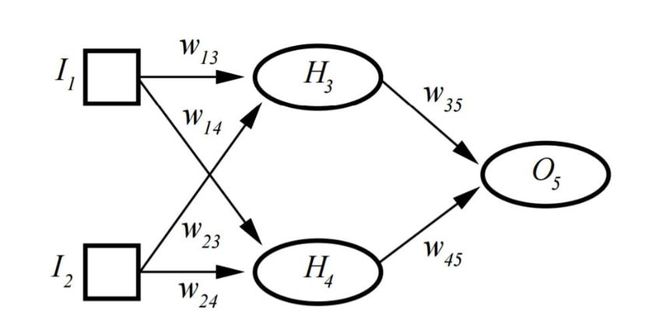
一种常见的多层结构的前馈网络（Multilayer Feedforward Network）由三部分组成，

• 输入层（Input layer），众多神经元（Neuron）接受大量非线形输入消息。输入的消息称为输入向量。
• 输出层（Output layer），消息在神经元链接中传输、分析、权衡，形成输出结果。输出的消息称为输出向量。
• 隐藏层（Hidden layer），简称“隐层”，是输入层和输出层之间众多神经元和链接组成的各个层面。隐层可以有一层或多层。隐层的节点（神经元）数目不定，但数目越多神经网络的非线性越显著，从而神经网络的强健性（robustness）（控制系统在一定结构、大小等的参数摄动下，维持某些性能的特性）更显著。习惯上会选输入节点1.2至1.5倍的节点。

  这种网络一般称为感知器（对单隐藏层）或多层感知器（对多隐藏层），神经网络的类型已经演变出很多种，这种分层的结构也并不是对所有的神经网络都适用。

下一篇文章我将详细的叙述如何训练人工神经网络

---

4 人工神经网络——学习过程概述

  在上述的感知机算法中，设定权重的工作，即确定合适的、能符合预期的输 入与输出的权重，现在还是由人工进行的。上一节中，我们结合与门、或门 的真值表人工决定了合适的权重。

神经网络的优势就在于它可以自动地从数据中学习到合适的权重参数。

---

4.1学习过程

  通过训练样本的校正，对各个层的权重进行校正（learning）而创建模型的过程，称为自动学习过程（training algorithm）。具体的学习方法则因网络结构和模型不同而不同，常用反向传播算法（Backpropagation/倒传递/逆传播，以output利用一次微分Delta rule来修正weight）来验证。

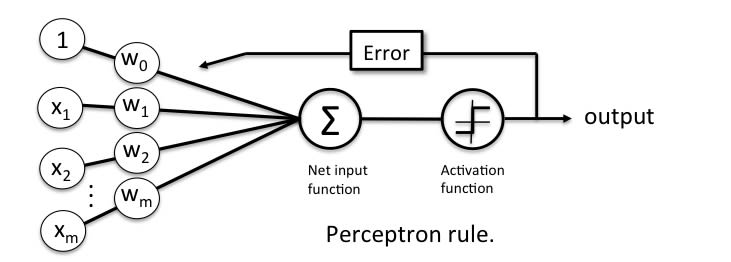
4.2 感知器学习规则

  Perceptron学习规则指出该算法将自动学习最佳权重系数。然后将输入要素与这些权重相乘，以确定神经元是否触发。

  感知器接收多个输入信号，并且如果输入信号的总和超过某个阈值，则它会输出信号或不返回输出。在监督学习和分类的情况下，这可以用来预测样本的类别。

如果你想要了解代码如何实现，请进入下一文，我将详细的推导运算过程。

---

总结

  本文详细的介绍了由生物学启发的人工神经网络思想，作为深度学习的入门材料，本专栏【深度学习 理论篇】中使用Python 3，尽量不依赖外部库或工具，带领读者从零创建一个经典的深度学习网络，使读者在此过程中逐步理解深度学习。

参考的资料：

1. 吴恩达《deeplearning.ai》课程
2. 斋藤康毅《深度学习入门：基于 Python 的理论与实现》
3. simplilearn《What is Perceptron: A Beginners Tutorial for Perceptron》