C:时间复杂度与空间复杂度
时间复杂度与空间复杂度
一、时间复杂度:执行一个算法,代码运行的次数和问题规模之间的函数关系,用O()表示
时间复杂度 = 递归总次数 * 每次递归的次数
O(1):常数项,与问题规模无关,如下:
例1:
{++x;s=0;} //f(n)=2=2*1 O(f(n))=O(1)计算一般的时间复杂度注意:
1.只保留最高阶项
2.不要系数
3.本质计算其运行次数
例2:
for (int i=1;i <= n;++i) //1:n
{
for (int j=1; j <= n;++j) //2:n+n+n+...+n=n^2(n个n相加)
{
C[i][j]=0; //3:n^2(等同2)
for(int k=1;k<=n;++k) //4:n^3
{
C[i][j]+=a[i][k]*b[k][j]; //5:n^3
}
}
}由上面这段代码,可得O(f(n))=O(n^3).
例3:
for(int i = 1;i < n ; i *= 2) //1 2 4 8 16 32 64 ...
//算最高项:2*2*2*2*2*2*...=n
//2^x=n
//x=log(2,n)(其中2为底数)例3 中的不一样处为,i *= 2,由上述注释算的O(f(n))=O(log(2,n))(其中2为底数,n为对数),以下表示的含义相同,可发现这种算法的速度是非常的快。在二分查找中,时间复杂度也是如此。
例4:判断素数
bool Fun(int n)
{
int i=2;
while ((n%i)!=0 && i*1.0sqrt(n)) //O(n^1/2)
return true;
else
return false;
} 例四的时间复杂度为O(n^1/2).
二、空间复杂度:执行一个算法,需要额外的辅助空间和问题规模之间的函数关系,用O()表示(浪费内存)
空间复杂度 = 递归的深度 * 每次递归空间的大小
递归深度:树的高度(递归的过程是一个“二叉树”)
归并排序中,额外加了数组,则它的空间复杂度为O(n).
例5:问学生a多少岁,a说,他比b大2岁;问学生b多少岁,b说,他比c大2岁;问学生c多少岁,c说,他比d大2岁;第五个学生说自己10岁,问a多少岁?(用递归解决问题)
#include
int Age (int n)
{
int tmp;
if(n==1)
tmp=10;
else
tmp=Age(n-1)+2;
return tmp;
}
int main ()
{
printf("%d\n",Age(5));
return 0;
}
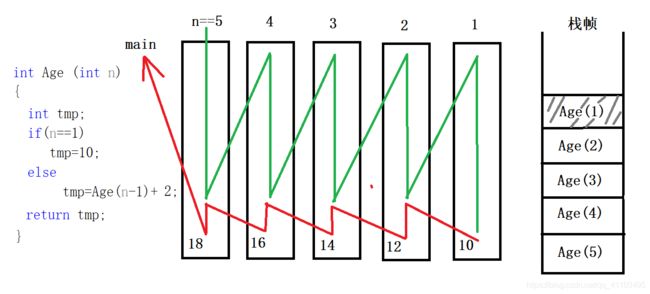
由例5 可看出,是典型的递归算法,其内部实现如图所示:
上图中,其中黑色矩形为实行Age(5)时,需要的内存,绿色的线为进去的时候,调用函数时,具体走到代码的哪个位置,与左边的代码是平行的,红色线是返回值的时候,最终答案18将给main函数,栈帧是用来保存每次调用下个函数之前,应将之前的步骤保存起来,而在走红线的时候,也就是返回值的时候,每个函数依次出栈,使得找到答案。综上,这个递归函数的空间复杂度为O(n).
例6:递归1,最普通的递归函数,由于额外占用内存与n有关,则空间复杂度为O(n).
int Fun(int n) //此递归时间复杂度为O(n),空间复杂度为O(n)
{
if(n <=1)
return n;
else
return Fun(n-1)+1;
}
例7:递归2,此递归特殊在,其中调用的函数为Fun(n/2),则求出时间复杂度与空间复杂度都为O(log(2,n)).
int Fun(int n) //此递归时间复杂度为O(log(2,n)),空间复杂度为O(log(2,n))
{
if(n <=1)
return n;
else
return Fun(n/2)+1;
}注意:空间复杂度如果太大,容易崩溃,最常见的是递归。
Windows 的栈空间 只有 1 M,若执行下面代码,则会崩溃,原因就是超出内存空间。
#include
int main ()
{
char arr[1024*1024];
printf("haha\n");
return 0;
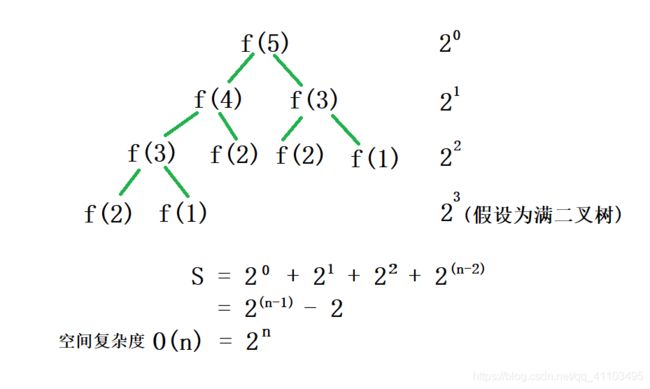
} 例8:斐波那契,最不适合递归的例子
//斐波那契 f(n) = f(n-1) + f(n-2)
int Fibno(int n)
{
if(n==1 || n==2)
return 1;
else
return Fibno(n-1)+Fibno(n-2);
}由例8可看出,斐波那契用递归的话,它的空间复杂度超级大,而如果用for循环的话,就会非常简单,因为它只占用了,几个变量的内存,所以空间复杂度为O(1).代码如下:
//斐波那契 f(n) = f(n-1) + f(n-2)
#include
int Fibno(int n)
{
int f1=1;
int f2=1;
int f3=0;
for(int i=2; i 编译如下:
例9:最适合递归的例子:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
代码如下:
#include
int g_count =0;
void Move (char x,char y)
{
g_count++;
printf("%c -> %c\n",x,y);
}
void Hanoi(int n,char a,char b,char c)
{
if(n == 1)
{
Move(a,c);
}
else
{
Hanoi(n-1,a,c,b);
Move(a,c);
Hanoi(n-1,b,a,c);
}
}
int main ()
{
Hanoi(5,'A','B','C');
printf("%d\n",g_count);
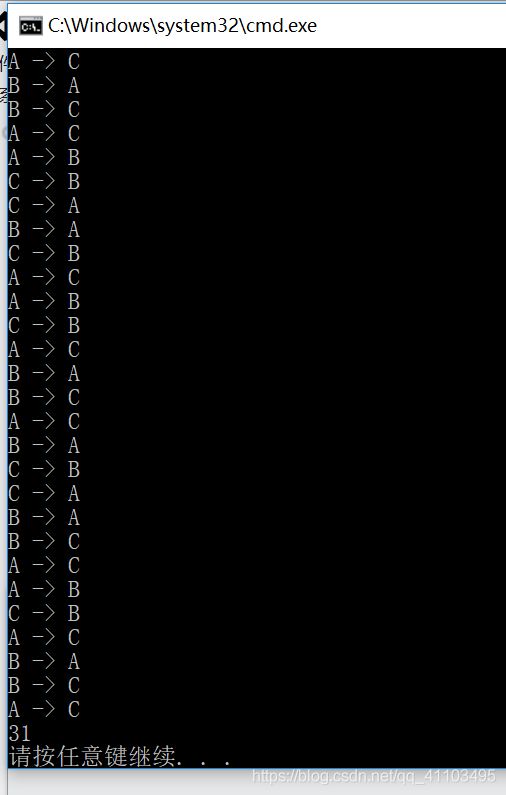
} 编译如下: 如果时候5块时,先是输出步骤,然后输出总共的次数为31。