Exp-Golomb指数哥伦布解码和编码

1,【H264/AVC 句法和语义详解】(五)：Exp-Golomb指数哥伦布编码（理论篇)

 https://blog.csdn.net/u011399342/article/details/80472399

公式如下:
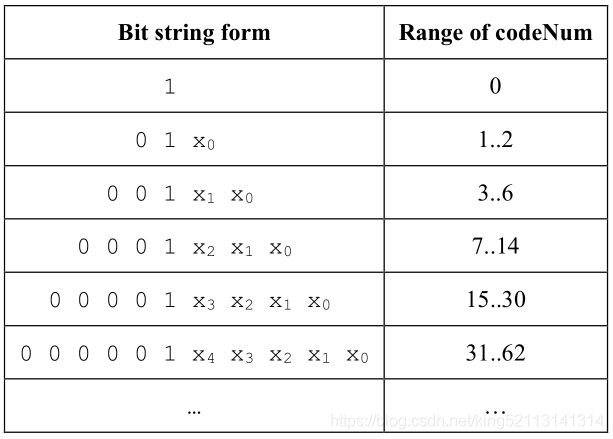
其中leadingZeroBits为1前面，0的个数。所以在解码的时候，如果遇到描述子为ue(v)，则可以先数0的个数，数到1为止，其中0的个数即为leadingZeroBits。而公式中的read_bits( leadingZeroBits )，则为从中间1开始，往后顺序数leadingZeroBits个比特位,将这几个比特位所表示的数值返回。

//ue(v)就代表了0阶指数哥伦布编码，通常被称为无符号指数哥伦布编码:

leadingZeroBits = −1
for (b = 0; !b; leadingZeroBits++)
    b = read_bits(1)
 
codeNum = 2^(leadingZeroBits) − 1 + read_bits(leadingZeroBits)


长度=2*leadingZeroBits+1

二进制比特串       长度          0阶指数哥伦布解码值
1001             1               0
001 1001         5               5
01 1010          3               2
010              3               1
000 1011         7               10
0001 001         7               8

利用上述公式，就可以计算出codeNum的值。

x0~x4可表示0或者1

2,Exponential-Golomb decoding

http://guoh.org/lifelog/2013/10/exp-golomb-coding/ 

 对于11110001 01100001 01100010 01100010进行哥伦布解码

过程就是读取1位，在这里结果是1，所以会跳出循环，但是leadingZeroBits++还是会执行，所以leadingZeroBits为0，后面read_bits也不会读取数据了。
codeNum = 2^0 – 1 + 0 = 0
也就是说编码为1的属性实际值为0
seq_parameter_set_id = 0 // Exp-Golomb解11110001中的第一个字码1

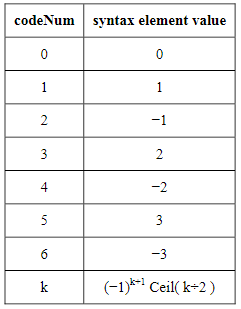
3,Se(v)

if the syntax element is coded as se(v), the value of the syntax element is derived by invoking the mapping process for signed Exp-Golomb codes as specified in ue(v) with codeNum as the input. 

4,Exponential-Golomb coding

https://en.wikipedia.org/wiki/Exponential-Golomb_coding

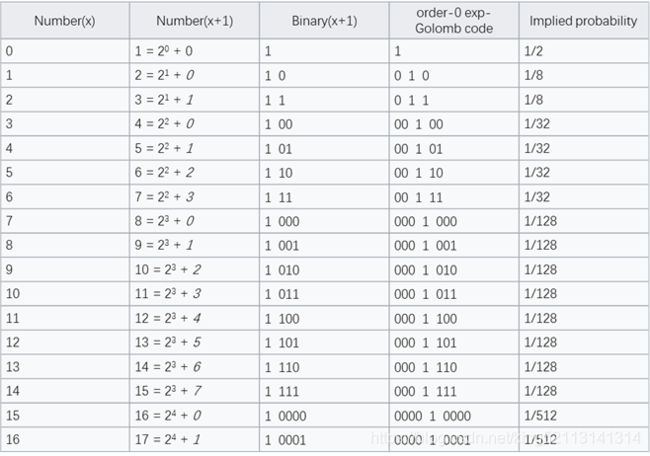
0阶哥伦布:

To code a number x ≥ 1:

1. Let 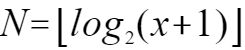 be the highest power of 2 it contains, so .
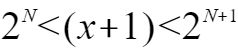2. Write out N zero bits, then
3. Append the binary form of (x+1), the binary form of (x+1) is an (N+1)-bit binary number.

An equivalent way to express the same process:  To encode any nonnegative integer x using the exp-Golomb code:

1. Write down x+1 in binary
2. Count the bits written, subtract one, and write that number of starting zero bits preceding the previous bit string.
3. 

k阶哥伦布:

To encode larger numbers in fewer bits (at the expense of using more bits to encode smaller numbers), this can be generalized using a nonnegative integer parameter  k. To encode a nonnegative integer x in an order-k exp-Golomb code:

第二步的删除前面的K个0,也可以改为在0阶指数哥伦布计算时不在前面写N个0,而是在前面写N-K个0

 

5,k阶哥伦布解码

leadingZeroBits = −1
for (b = 0; !b; leadingZeroBits++)
    b = read_bits(1)
 
codeNum = 2^(leadingZeroBits + k) − 2^k + read_bits(leadingZeroBits + k)