TF学习：Tensorflow基础案例、经典案例集合——基于python编程代码的实现

TF学习：Tensorflow基础案例、经典案例集合——基于python编程代码的实现

 

目录

Tensorflow的使用入门

1、TF：使用Tensorflow输出一句话

2、TF实现加法

3、TF实现乘法

4、TF实现计算功能

5、TF：Tensorflow完成一次线性函数计算

Tensorflow的基础案例

1、TF根据三维数据拟合平面

Tensorflow的经典案例

---

 

 

 

相关文章
TF学习——DL框架之Tensorflow：Tensorflow的简介、安装、使用方法之详细攻略

 

Tensorflow的使用入门

1、TF：使用Tensorflow输出一句话

#TF：使用Tensorflow输出一句话
import tensorflow as tf
import numpy as np

greeting = tf.constant('Hello Google Tensorflow!')
sess = tf.Session()           #启动一个会话
result = sess.run(greeting)   #使用会话执行greeting计算模块
print(result) 
sess.close()                  #关闭会话，这是一种显式关闭会话的方式

 

2、TF实现加法

张量和图的两种方式实现：声明两个常量 a 和 b，并定义一个加法运算。先定义一张图，然后运行它，

# -*- coding: utf-8 -*-

#1、张量和图的两种方式实现：声明两个常量 a 和 b，并定义一个加法运算。先定义一张图，然后运行它，
import tensorflow as tf
import os
import numpy as np
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' 

#T1
a=tf.constant([1,0,1,4]) 
b=tf.constant([ 1 , 0 , 0 , 4 ]) 
result=a+b 
sess=tf. Session () 
print (sess.run(result)) 
sess.close
#T2
with  tf.Session()  as  sess:
    a=tf.constant([ 1 , 0 , 1 , 4 ])
    b=tf.constant([ 1 , 0 , 0 , 4 ])
    result=a+b
    print (sess.run(result))


#2、常量和变量
#TensorFlow 中最基本的单位是常量（Constant）、变量（Variable）和占位符（Placeholder）。常量定义后值和维度不可变，变量定义后值可变而维度不可变。在神经网络中，变量一般可作为储存权重和其他信息的矩阵，而常量可作为储存超参数或其他结构信息的变量。下面我们分别定义了常量与变量
#声明了不同的常量（tf.constant()）
a = tf.constant( 2 , tf.int16)  #声明了不同的整数型数据
b = tf.constant( 4 , tf.float32)  #声明了不同的浮点型数据
c = tf.constant( 8 , tf.float32)  
#声明了不同的变量（tf.Variable()）
d = tf. Variable ( 2 , tf.int16) 
e = tf. Variable ( 4 , tf.float32)  
f = tf. Variable ( 8 , tf.float32)   

g = tf.constant(np.zeros(shape=( 2 , 2 ), dtype=np.float32))#声明结合了 TensorFlow 和 Numpy 

h = tf.zeros([ 11 ], tf.int16)  #产生全是0的矩阵
i = tf.ones([ 2 , 2 ], tf.float32)  #产生全是 1的矩阵
j = tf.zeros([ 1000 , 4 , 3 ], tf.float64)  
k = tf. Variable (tf.zeros([ 2 , 2 ], tf.float32))  
l = tf. Variable (tf.zeros([ 5 , 6 , 5 ], tf.float32))

#声明一个 2 行 3 列的变量矩阵，该变量的值服从标准差为 1 的正态分布，并随机生成
w1=tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
#TensorFlow 还有 tf.truncated_normal() 函数，即截断正态分布随机数，它只保留 [mean-2*stddev,mean+2*stddev] 范围内的随机数
#案例应用：应用变量来定义神经网络中的权重矩阵和偏置项向量
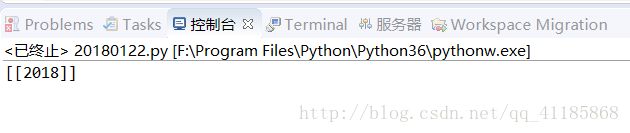
weights = tf.Variable(tf.truncated_normal([256 * 256, 10])) 
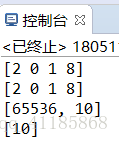
biases = tf. Variable (tf.zeros([10])) 
print (weights.get_shape().as_list()) 
print (biases.get_shape().as_list())

 

3、TF实现乘法

Tensorflow之session会话的使用，定义两个矩阵，两种方法输出2个矩阵相乘的结果

import tensorflow as tf

matrix1 = tf.constant([[3, 20]]) 
matrix2 = tf.constant([[6],      
                       [100]])
product = tf.matmul(matrix1, matrix2)  

# method 1，常规方法
sess = tf.Session()        
result = sess.run(product)
print(result)
sess.close()             

# # method 2，with方法
# with tf.Session() as sess:   #
#     result2 = sess.run(product)
#     print(result2)

 

4、TF实现计算功能

TF：Tensorflow定义变量+常量,实现输出计数功能

输出结果

代码设计

#TF：Tensorflow定义变量+常量,实现输出计数功能

import tensorflow as tf

state = tf.Variable(0, name='Parameter_name_counter')  
#print(state.name)
one = tf.constant(1)   

new_value = tf.add(state, one)  
update = tf.assign(state, new_value)

init = tf.global_variables_initializer()  

with tf.Session() as sess:  
    sess.run(init)        
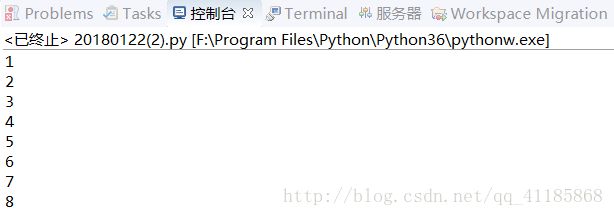
    for _ in range(8):
        sess.run(update)
        print(sess.run(state))

 

5、TF：Tensorflow完成一次线性函数计算

#TF：Tensorflow完成一次线性函数计算
#思路：TF像搭积木一样将各个不同的计算模块拼接成流程图，完成一次线性函数的计算，并在一个隐式会话中执行。
matrix1 = tf.constant([[3., 3.]])           #声明matrix1为TF的一个1*2的行向量
matrix2 = tf.constant([[2.],[2.]])          #声明matrix2为TF的一个2*1的列向量
product = tf.matmul(matrix1, matrix2)       #两个算子相乘，作为新算例
linear = tf.add(product, tf.constant(2.0))  #将product与一个标量2求和拼接.作为最终的linear算例

#直接在会话中执行linear算例，相当于将上面所有的单独算例拼接成流程图来执行
with tf.Session() as sess:
    result = sess.run(linear)
    print(result)

 

 

Tensorflow的基础案例

1、TF根据三维数据拟合平面

Python 程序生成了一些三维数据, 然后用一个平面拟合它.

import tensorflow as tf
import numpy as np

# 使用 NumPy 生成假数据(phony data), 总共 100 个点.
x_data = np.float32(np.random.rand(2, 100)) # 随机输入
y_data = np.dot([0.100, 0.200], x_data) + 0.300

# 构造一个线性模型
# 
b = tf.Variable(tf.zeros([1]))
W = tf.Variable(tf.random_uniform([1, 2], -1.0, 1.0))
y = tf.matmul(W, x_data) + b

# 最小化方差
loss = tf.reduce_mean(tf.square(y - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)

# 初始化变量
init = tf.initialize_all_variables()

# 启动图 (graph)
sess = tf.Session()
sess.run(init)

# 拟合平面
for step in xrange(0, 201):
    sess.run(train)
    if step % 20 == 0:
        print step, sess.run(W), sess.run(b)

# 得到最佳拟合结果 W: [[0.100  0.200]], b: [0.300]

 

 

Tensorflow的经典案例

后期更新……