实 验 报 告
课程:程序设计与数据结构
姓名:杨京典
班级:1623
学号:20162302
实验名称:查找与排序
实验器材:装有IdeaU的联想拯救者15ISK
实验目的与要求:
1.完成
Searching.Java及Sorting.java中方法的测试
2.重构代码
3.在Searching中补充查找算法并测试
4.在Sorting中补充实现课上讲过的排序方法
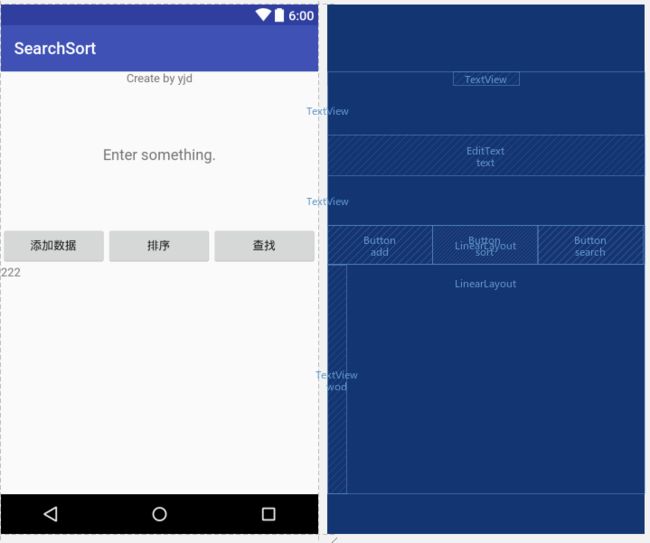
5.编写Android程序对各种查找与排序算法进行测试
实验内容、步骤与体会:
实验内容:
完成
Searching.Java及Sorting.java中方法的测试SeaSorTest
在测试中要有正常,异常,边界,正序,逆序的情况
在
Searching类里面,有两个查找方法:线性查找linearSearch()和二分查找binarySearch()。其中binarySearch()对于有序数据才有用。所以在建立数据的时候可以专门建立一组有序的数据来供它使用,也可以提前调用Sorting中的方法将数据排序构建数据,建立多种类型的数据以测试泛型的实现是否成功
String[] data1 = {"3", "1", "4", "1", "5", "9", "2", "20162302"};
Integer[] data2 = {20162302, 2, 5, 8, 95, 3, 6, 5, 2, 6, 7};
Character[] data3 = {'2', '0', '1', '6', '2', '3', '0', '2', '2', '4'};
Integer[] data4 = {1, 2, 3, 4, 5, 7, 8, 11, 56, 2302}测试正常情况,搜索已存在的数据
System.out.println(searching.linearSearch(data1, "20162302"));
System.out.println(searching.binarySearch(data4, 20162302));测试异常情况,搜索不存在的数据
System.out.println(searching.linearSearch(data2, 34));
System.out.println(searching.binarySearch(data4, 44));测试边界情况,搜索首位及末尾数据
System.out.println(seaching.linearSearch(data1,"3");
System.out.println(seaching.binarySearch(data4,2302);
System.out.println(seaching.binarySearch(data4,1);在
Sorting类里面,有五个排序方法选择排序selectionSort,插入排序insertionSort,冒泡排序bubbleSort,快速排序quickSort和归并排序mergeSort。由于每次排序都会对原来的数据造成损坏,所以每次测试都要重新创建数据。(为节省篇幅,这里只举出冒泡排序法的测试)测试正常情况
data1 = {"3", "1", "4", "1", "5", "9", "2", "20162302"};
sorting.bubbleSort(data1);测试异常情况,排列只有一个元素的数据以及没有元素的数据
data1 = {"1"};
sorting.bubbleSort(data1);
data1 = {};
sorting.bubbleSort(data1);测试边界情况,排列有序数据
sorting.bubbleSort(data4);增加方法,测试逆序情况
public static void diaBubbleSort(Comparable[] data) {
int position, scan;
for (position = data.length - 1; position >= 0; position--) {
for (scan = 0; scan <= position - 1; scan++)
if (data[scan].compareTo(data[scan + 1]) < 0)
swap(data, scan, scan + 1);
}
} data1 = {"3", "1", "4", "1", "5", "9", "2", "20162302"};
sorting.diaBubbleSort(data1); for (int i = 0; i < data1.length; i++)
System.out.print(data1[i]+" ");
System.out.println();重构代码到包
cn.edu.besti.cs1623.yjd2302和包test
把Sorting.java Searching.java放入cn.edu.besti.cs1623.(姓名首字母+四位学号) 包中,把测试代码放test包中,重新编译,运行代码。对于重构,有两种方法可以做到
第一种方法是在IDEA里面实现的
首先在项目里面找到src点击右键打开快捷菜单选择new→package
然后输入包的名称
然后找到需要移动的代码,点击右键打开快捷菜单选择Refactor→Move
最后在To package里面输入新建的包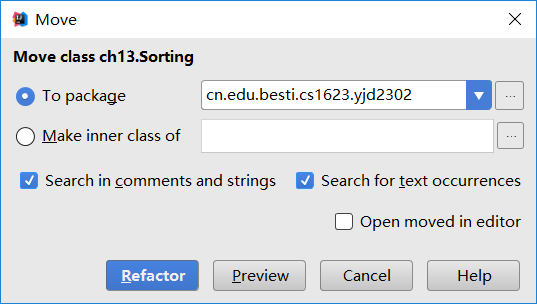
第二种方法可以脱离IDEA
打开项目的src,直接在里面创建文件夹cn
打开cn创建edu
以此类推创建一系列文件夹
然后把代码复制或剪切进来
最后把最前面的包名改成刚刚创建的
在
Searching中补充查找算法并测试
参考七大查找算法在Searching中补充查找算法并测试
- 插值算法。帖子里面给出的源码都是c++的
int InsertionSearch(int a[], int value, int low, int high)
{
int mid = low+(value-a[low])/(a[high]-a[low])*(high-low);
if(a[mid]==value)
return mid;
if(a[mid]>value)
return InsertionSearch(a, value, low, mid-1);
if(a[mid]但是在c++里面有很多和java是相同的,这个里面只应用到了简单的符号运算以及if判断,所以在java里面也可以直接使用,使其变成public即可
public int insertionSearch(int a[], int value, int low, int high) {
int mid = low + (value - a[low]) / (a[high] - a[low]) * (high - low);
if (a[mid] == value)
return mid;
if (a[mid] > value)
return insertionSearch(a, value, low, mid - 1);
if (a[mid] < value)
return insertionSearch(a, value, mid + 1, high);
else
return 0;
}斐波那契查找
基本思想:也是二分查找的一种提升算法,通过运用黄金比例的概念在数列中选择查找点进行查找,提高查找效率。同样地,斐波那契查找也属于一种有序查找算法。
相对于折半查找,一般将待比较的key值与第mid=(low+high)/2位置的元素比较,比较结果分三种情况:
1)相等,mid位置的元素即为所求
2)>,low=mid+1;
3)<,high=mid-1。
斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,及n=F(k)-1;
开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种
1)相等,mid位置的元素即为所求
2)>,low=mid+1,k-=2;
说明:low=mid+1说明待查找的元素在[mid+1,high]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个,所以可以递归的应用斐波那契查找。
3)<,high=mid-1,k-=1。
说明:low=mid+1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个,所以可以递归 的应用斐波那契查找。
我将构建斐波那契数组的方法合并到查找方法里面
int[] F = new int[max_size];
F[0] = 1;
F[1] = 1;
for (int i = 2; i < max_size; ++i)
F[i] = F[i - 1] + F[i - 2];
//构造一个斐波那契数组F在java中为了达到复制数组中的数据的目的
Integer[] temp = new Integer[F[k] - 1];//将数组a扩展到F[k]-1的长度
for (int i = 0; i < a.length; i++)
temp[i] = a[i];树表查找
基本思想:二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
在之前的学习中已经有完成的二叉查找树的代码,可以在这里直接调用。
public int binarySearchTree(int[] data, int a){
LinkedBinarySearchTree binarySearchTree = new LinkedBinarySearchTree();
for (int i = 0; i < data.length; i++)
binarySearchTree.add(data[i]);
if(binarySearchTree.find(a)==null)
return -1;
else
return a;
}哈希查找
算法思想:哈希的思路很简单,如果所有的键都是整数,那么就可以使用一个简单的无序数组来实现:将键作为索引,值即为其对应的值,这样就可以快速访问任意键的值。这是对于简单的键的情况,我们将其扩展到可以处理更加复杂的类型的键。
建立一个哈希表,然后把数据放进去,以数字为键,查找时检索整个哈希表
public int hashSearch(int[] data, int a){
boolean result = false;
HashMap hashMap = new HashMap();
for(int i = 0; i 在
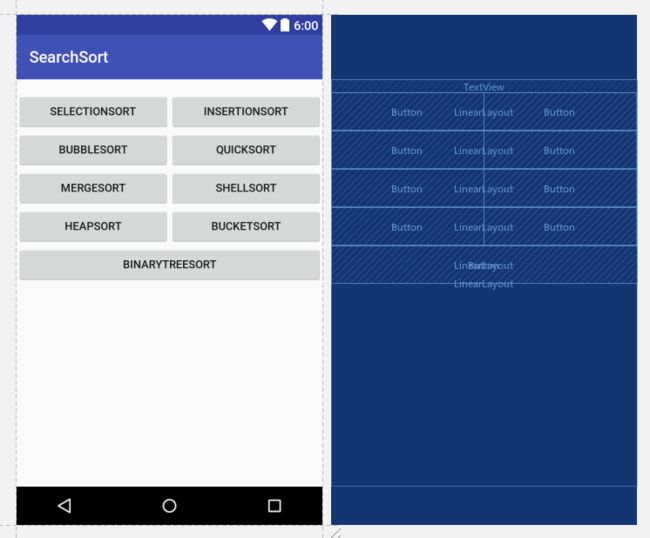
Sorting中补充实现课上讲过的排序方法
补充实现课上讲过的排序方法:希尔排序,堆排序,桶排序,二叉树排序等。
- 希尔排序,先取一个小于n的整数d1作为第一个 增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行 直接插入排序;然后,取第二个增量d2。
//希尔排序
public void shellSort(Comparable[] data) {
int d = data.length;
while (d!=1) {
d = d / 2;
for (int i = 0; i < d; i++) {
for (int j = i + d; j < data.length; j = j + d) {
Comparable temp = data[j];
int x;
for (x = j - d; x >= 0 && data[x].compareTo(temp) > 0; x = x - d)
data[x + d] = data[x];
data[x + d] = temp;
}
}
}
}- 堆排序,可以运用堆顶部元素总是为最大元素的特性来获取最大值
//堆排序
public void heapSort(Comparable[] data){
Comparable[] result = data;
LinkedMaxHeap linkedMaxHeap = new LinkedMaxHeap();
for (int i = 0; i < result.length; i++)
linkedMaxHeap.add(result[i]);
for (int i = result.length-1; i>=0;i--)
data[i]=linkedMaxHeap.removeMax();
}- 桶排序
参考资料:计数排序和桶排序(Java实现)
根据数据的范围对这些范围进行分成几个大桶,然后再逐一给大桶里面的数据排序。代码中大致的思路体现出来了,就是不能支持泛型,所以就要对这一部分进行优化。在Comparable中的Compureto()是对两个元素进行比较,并返回差距值,可以理解为做差,这样就可以获取最小值和最大值。
//桶排序
public void bucketSort(Comparable[] data){
Comparable max = data[0];
Comparable min = data[0];
for(int i = 0; i < data.length; i++){
if(max.compareTo(data[i])<0)
max = data[i];
if (min.compareTo(data[i])>0)
min = data[i];
}
//桶数
int bucketNum = (max.compareTo(min)) / data.length + 1;
ArrayList> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){
bucketArr.add(new ArrayList());
}
//将每个元素放入桶
for(int i = 0; i < data.length; i++){
int num = (data[i].compareTo(min)) / (data.length);
bucketArr.get(num).add(data[i]);
}
//对每个桶进行排序
for(int i = 0; i < bucketArr.size(); i++)
Collections.sort(bucketArr.get(i));
int x =0;
for (int i =0; i - 二叉树排序,把数据放到树里面,获取最小值然后删除最小值,然后再获取最小值。
//二叉树排序
public void binaryTreeSort(Comparable[] data){
LinkedBinarySearchTree linkedBinarySearchTree = new LinkedBinarySearchTree();
for (int i = 0; i < data.length; i++)
linkedBinarySearchTree.add(data[i]);
for (int i = 0; i < data.length; i++) {
data[i] = linkedBinarySearchTree.findMin();
linkedBinarySearchTree.remove(linkedBinarySearchTree.findMin());
}
}- 测试方法
public class TestF {
public static void main(String[] args) {
int[] data1 = {2302, 2, 5, 8, 95, 3, 6, 5, 2, 6, 7};
Integer[] data2 = {2, 2, 3, 5, 5, 6, 6, 7, 8, 95, 2302};
Searching searching = new Searching();
System.out.println(searching.insertionSearch(data1,8,2,0));
System.out.println(searching.FibonacciSearch(data2,95));
System.out.println(searching.binarySearchTree(data1, 2302));
System.out.println(searching.hashSearch(data1, 6));
}
}
public class TestS {
public static void main(String[] args) {
Integer[] data1 = {2302, 2, 5, 8, 95, 3, 6, 5, 2, 6, 7};
Sorting sorting = new Sorting();
sorting.shellSort(data1);
for (int i = 0; i < data1.length; i++)
System.out.print(data1[i]+" ");
System.out.println();
Integer[] data2 = {2302, 2, 5, 8, 95, 3, 6, 5, 2, 6, 7};
sorting.heapSort(data2);
for (int i = 0; i < data1.length; i++)
System.out.print(data2[i]+" ");
System.out.println();
Integer[] data3 = {2302, 2, 5, 8, 95, 3, 6, 5, 2, 6, 7};
sorting.bucketSort(data3);
for (int i = 0; i < data3.length; i++)
System.out.print(data3[i]+" ");
System.out.println();
Integer[] data4 = {2302, 2, 5, 8, 95, 3, 6, 5, 2, 6, 7};
sorting.binaryTreeSort(data4);
for (int i = 0; i < data4.length; i++)
System.out.print(data4[i]+" ");
}
}编写Android程序对各种查找与排序算法进行测试
- 可以直接在按下跳转按钮的时候传送数据
Button button1 = (Button) findViewById(R.id.search);
button1.setOnClickListener(new View.OnClickListener() {
@Override
public void onClick(View v) {
String data = editText.getText().toString();
Intent intent = new Intent(MainActivity.this, Search.class);
intent.putExtra("extra_data", data);
startActivity(intent);
}
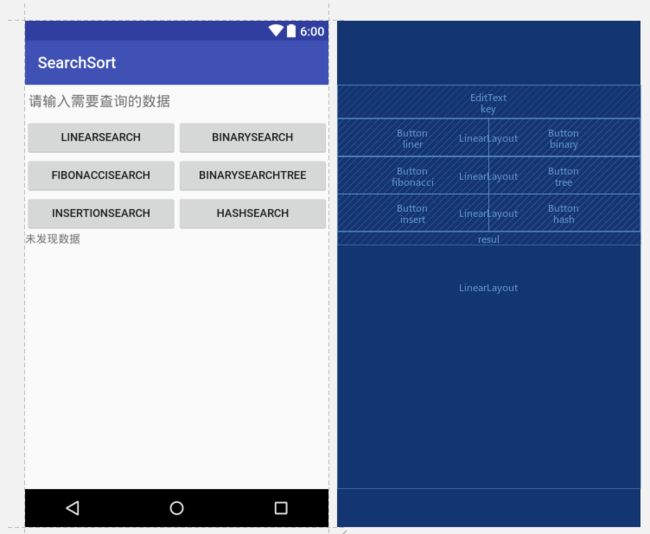
});- 对于
Search及Sort界面大量的按钮可以通过Switch来统一管理
public void onClick(View v) {
switch (v.getId()) {
case:
break;
}