学习之旅-红黑树之删除
前人栽树,后人乘凉。关于这样红黑树的帖子已经很多。我就不再重复造轮子了。我自己发现一个删除说的很好的博客,链接:http://gengning938.blog.163.com/blog/static/1282253812011420103852696/
我只是说说自己的理解。方便以后自己回来忘了的时候,能很快看懂。
分为几种情况:
1、删除的是叶子节点。那么,如果是红色,直接删除。如果是黑色,则这条分支少了一个黑色节点。需要调整。
2、删除的不是叶子节点,那么从他的右子树中找一个最小的节点和他交换,然后要删除的点就移到了叶子节点,回到情况1。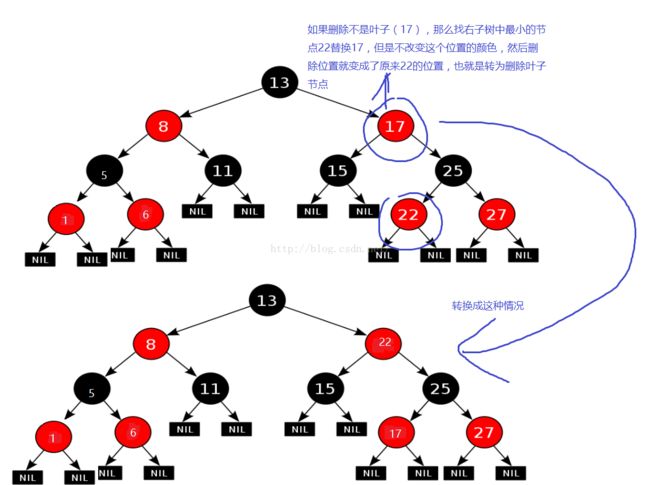
那么这个时候回到情况1了。这个运气好是红色的。但是如果是删除黑色的点呢?比如删除根节点13 。
如果删除的是13,那么右子树最小的是15,交换13和15。然后删除位置变为15。这个时候要删除的是黑色的节点,那就复杂了。又可以分为下面几种情况
1、删除的点的兄弟是红色,那么他的父亲,孩子都是黑色。这一种,交换兄弟与父亲的颜色,然后以父节点为准,旋转树,旋转之后新的兄弟变成了黑色。。转到下一种情况
2、删除的点的兄弟是黑色。又可以分为几种情况:
1)、黑色的兄弟的孩子都是黑色,那么把兄弟染成红色,这样,兄弟子树和自己都少了一个黑色节点,兄弟子树和自己平衡了。但是整个子树又比其他子树少了一个黑色,所以需要看父亲节点是红色还是黑色,如果父亲是红色,直接染黑就完全平衡了,但是父亲节点如果是黑色,那就继续看父亲的兄弟颜色。。
2)、黑色的兄弟孩子有红色的。那么如果远亲侄子是红色,那么远亲侄子染成黑色,交换父亲与兄弟的颜色,然后以父亲为准,根据删除点是父亲的左孩子还是右孩子进行相应的旋转,如果是左孩子就左旋,如果是右孩子就右旋。最后平衡。
3)、如果黑色的兄弟的远亲侄子是红色,那就转换为2)的情况。
所以复杂的情况就是四种,第1种,和第二种的三种情况。
以下是代码,写的时候参照了一下STL :
void tst_rbt_delete(tst_rbtree* tree, tst_rbtnode* node)
{
tst_rbtnode **root, *subt, *temp, *sentinel, *w;
root = &tree->root;
sentinel = tree->sentinel;
/*二叉树的删除*/
//找到要删除的节点。
if (sentinel == node->lchild) //fd1
{
subt = node->rchild;
temp = node;
}
else if (sentinel == node->rchild) //fd2
{
subt = node->lchild;
temp = node;
}
else //fd3
{
//node的左右孩子都不为空,那么从右子树中找到key最小的节点,交换node和这个点,再删除node
temp = tst_rbt_min_node(node->rchild, sentinel);
if (temp->lchild == sentinel)
{
//既然是最小的节点,其实并不会进入这个分支,如果还有左孩子,肯定不是最小的
subt = temp->rchild;
}
else
{
subt = temp->lchild;
}
}
//如果要删除的点是根节点,这种情况只会是fd1,fd2中的一种
if (temp == *root)
{
*root = subt;
tst_rbt_set_black(subt);
tst_rbt_node_reset(node);
return;
}
unsigned char isRed = tst_rbt_is_red(temp);
//把找到的节点移出树外。孩子上提
if (tst_rbt_is_lchild(temp))
{
tst_rbt_parent(temp)->lchild = subt;
}
else
{
tst_rbt_parent(temp)->rchild = subt;
}
if (temp == node)
{
//如果要删除的点就是node,那么node已经被移出树外
subt->parent = temp->parent;
}
else
{
//如果要删除的点不是node,而是右子树中最小的节点
if (node == tst_rbt_parent(temp))
{
//如果node是temp的父节点,那么,subt的父节点还是temp,但是如果subt是sentinel,那么sentinel一开始parent是NULL
subt->parent = temp;
}
else
{
//如果不是,那么subt的父节点该是temp的父节点
subt->parent = temp->parent;
}
temp->parent = node->parent;
temp->lchild = node->lchild;
temp->rchild = node->rchild;
tst_rbt_copy_color(temp, node);
if (node == *root)
{
//如果node是根,设置根为找到的节点
*root = temp;
}
else
{
//把找到的点替换node
if (tst_rbt_is_lchild(node))
{
tst_rbt_parent(node)->lchild = temp;
}
else
{
tst_rbt_parent(node)->rchild = temp;
}
}
if (!tst_rbt_is_leaf(tree, temp->lchild))
{
temp->lchild->parent = temp;
}
if (!tst_rbt_is_leaf(tree, temp->rchild))
{
temp->rchild->parent = temp;
}
}
tst_rbt_node_reset(node);
if (isRed)
{
return;
}
//dsptree(*root, sentinel);//打印树
/* 重新平衡红黑树 */
while (subt != *root && tst_rbt_is_black(subt))
{
if (tst_rbt_is_lchild(subt))
{
w = tst_rbt_parent(subt)->rchild;
/*复杂情况1:
*兄弟是红色,那么父节点,兄弟的孩子都是黑色。交换兄弟与父亲的颜色
*然后左旋。转换情况为要删除的点的兄弟是黑色。
*/
if (tst_rbt_is_red(w))//w是红色。则w的parent,child必然是黑色
{
tst_rbt_set_red(tst_rbt_parent(subt));
tst_rbt_set_black(w);
tst_rbt_rotate_left(root, tst_rbt_parent(subt), sentinel);
w = tst_rbt_parent(subt)->rchild;//转化为subt的兄弟是黑色的情况
}
/*复杂情况2:
*如果要删除的点的兄弟不是红色,并且兄弟的左右孩子都是黑色
*那么把兄弟染成红色,再看父节点。如果是红色,跳出循环,最后染成黑色,ok
*如果父节点是黑色,那么又回到最原始的问题(情况1234都可能)
*/
if (tst_rbt_is_black(w->lchild) && tst_rbt_is_black(w->rchild))
{
tst_rbt_set_red(w);
subt = tst_rbt_parent(subt);
}
else
{
/*复杂情况3:兄弟节点有红色孩子
*如果兄弟的远侄子是黑色,那么肯定近亲侄子是红色。
*最终目的是把远侄子变成红色,转换成下一种情况,可以最终解决问题。
*/
if (tst_rbt_is_black(w->rchild))
{
tst_rbt_set_black(w->lchild);
tst_rbt_set_red(w);
tst_rbt_rotate_right(root, w, sentinel);
w = tst_rbt_parent(subt)->rchild;
}
/*复杂情况4:
*如果远侄子是红色,直接把远侄子设为黑色,交换父亲与兄弟颜色
*最终选择合适的旋转方向旋转子树。达到平衡。
*/
tst_rbt_copy_color(w, tst_rbt_parent(subt));
tst_rbt_set_black(tst_rbt_parent(subt));
tst_rbt_set_black(w->rchild);
tst_rbt_rotate_left(root, tst_rbt_parent(subt), sentinel);
subt = *root;//结束循环,同时方便后续设置根节点为黑色
}
}
else
{
//与上面,删除点是父亲的左孩子相似,只不过,旋转树的时候方向与上面情况相反
w = tst_rbt_parent(subt)->lchild;
if (tst_rbt_is_red(w))//w是红色。w的parent,child必然是黑色
{
tst_rbt_set_black(w);
tst_rbt_set_red(tst_rbt_parent(subt));
tst_rbt_rotate_right(root, tst_rbt_parent(subt), sentinel);
w = tst_rbt_parent(subt)->lchild;
}
if (tst_rbt_is_black(w->lchild) && tst_rbt_is_black(w->rchild))
{
tst_rbt_set_red(w);
subt = tst_rbt_parent(subt);
}
else
{
if (tst_rbt_is_black(w->lchild))
{
tst_rbt_set_red(w);
tst_rbt_set_black(w->rchild);
tst_rbt_rotate_left(root, w, sentinel);
w = tst_rbt_parent(subt)->lchild;
}
tst_rbt_copy_color(w, tst_rbt_parent(subt));
tst_rbt_set_black(tst_rbt_parent(subt));
tst_rbt_set_black(w->lchild);
tst_rbt_rotate_right(root, tst_rbt_parent(subt), sentinel);
subt = *root;
}
}
//dsptree(*root, sentinel);//打印树
}
tst_rbt_set_black(subt);
}