C语言实现FFT并与DFT比较(徐士良老师编写的c语言算法程序)
一 . FFT方法说明
计算n个采样点
的傅里叶变换,可以归结为计算多项式 :
在各n次单位根1,w,w 2,…,w n-1上的值,即
其中, w= e − j 2 π N {\rm e}^{-j\frac{2π}{N}} e−jN2π 为n次单位元根.
若n是2的k次幂,即 n=2 k (k>0), 则f(x)可以分解为关于x的的奇次幂和偶次幂两部分,即:
若令
则有
并且有
由此可以看出,为了求f(x)在各n次单位根上的值,只需求 Peven(x2) 和 x Podd(x2)在1,w 2,…,(w (n/2)-1) 2上的值就可以了。
而Peven 和 Podd同样可以分解成关于x2的偶次幂和奇次幂两部分。依此类推,
一直分解下去,最后可以归纳为只需求2次单位根1与-1上的值。
在实际计算时,可以将上述过程倒过来计算,这就是FFT算法。
二 . C语言实现FFT
1.函数语句与形参说明
void kfft (pr,pi,n,k,fr,fi,il)
| 形参与函数类型 | 参数意义 |
|---|---|
| double pr[n] | 存放n个采样输入的实部,返回离散傅里叶变换的摸 |
| double pi[n] | 存放n个采样输入的虚部 |
| double fr[n] | 返回离散傅里叶变换的n个实部 |
| double fi[n] | 返回离散傅里叶变换的n个虚部 |
| int n | 采样点数 |
| int k | 满足n=2k |
| void kfft() | 过程 |
2.FFT源程序(以徐士良老师编写的c程序为例)
#include "math.h"
void kfft(pr,pi,n,k,fr,fi)
int n,k;
double pr[],pi[],fr[],fi[];
{
int it,m,is,i,j,nv,l0;
double p,q,s,vr,vi,poddr,poddi;
for (it=0; it<=n-1; it++) //将pr[0]和pi[0]循环赋值给fr[]和fi[]
{
m=it;
is=0;
for(i=0; i<=k-1; i++)
{
j=m/2;
is=2*is+(m-2*j);
m=j;
}
fr[it]=pr[is];
fi[it]=pi[is];
}
pr[0]=1.0;
pi[0]=0.0;
p=6.283185306/(1.0*n);
pr[1]=cos(p); //w=e^-j2pi/n欧拉公式表示
pi[1]=-sin(p);
for (i=2; i<=n-1; i++) //计算pr[]
{
p=pr[i-1]*pr[1];
q=pi[i-1]*pi[1];
s=(pr[i-1]+pi[i-1])*(pr[1]+pi[1]);
pr[i]=p-q; pi[i]=s-p-q;
}
for (it=0; it<=n-2; it=it+2)
{
vr=fr[it];
vi=fi[it];
fr[it]=vr+fr[it+1];
fi[it]=vi+fi[it+1];
fr[it+1]=vr-fr[it+1];
fi[it+1]=vi-fi[it+1];
}
m=n/2;
nv=2;
for (l0=k-2; l0>=0; l0--) //蝶形计算
{
m=m/2;
nv=2*nv;
for (it=0; it<=(m-1)*nv; it=it+nv)
for (j=0; j<=(nv/2)-1; j++)
{
p=pr[m*j]*fr[it+j+nv/2];
q=pi[m*j]*fi[it+j+nv/2];
s=pr[m*j]+pi[m*j];
s=s*(fr[it+j+nv/2]+fi[it+j+nv/2]);
poddr=p-q;
poddi=s-p-q;
fr[it+j+nv/2]=fr[it+j]-poddr;
fi[it+j+nv/2]=fi[it+j]-poddi;
fr[it+j]=fr[it+j]+poddr;
fi[it+j]=fi[it+j]+poddi;
}
}
for (i=0; i<=n-1; i++)
{
pr[i]=sqrt(fr[i]*fr[i]+fi[i]*fi[i]); //计算幅值
}
return;
}
3.进行傅里叶变换
正弦波表达式为: s(t) = 0.6 sin( 2π 50t ) 和s(t) = 0.6 sin( 2π 500t )
(为便于计算,我们将采样频率8000次近似设为8192次)
#include "stdio.h"
#include "math.h"
#include "kfft.c"
#define PI 3.1415926535
main()
{
int i,j;
double pr[8192],pi[8192],fr[8192],fi[8192],t[8192];
for (i=0; i<=8191; i++)
{
t[i] = i*0.001;
pr[i]=0.6*sin(2*PI*50*t[i])+0.6*sin(2*PI*500*t[i]); pi[i]=0.0;
}
kfft(pr,pi,8192,13,fr,fi); //调用FFT函数
for (i=0; i<8192; i++)
{
printf("%d\t%lf\n",i,pr[i]);
}
}
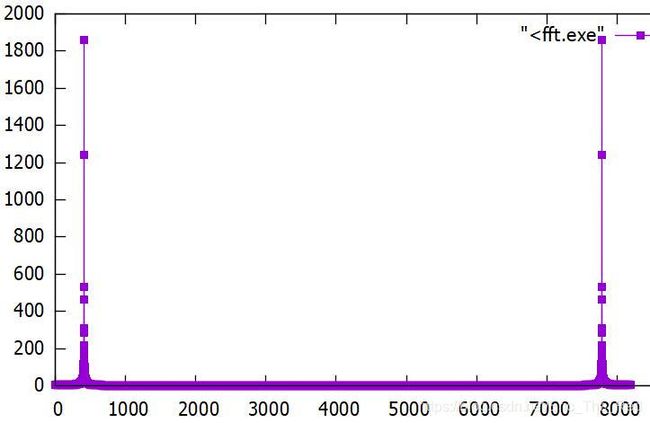
4.用gnuplot作图
将FFT.c在控制台编译后,用gnuplot作图:
一般来说,FFT比DFT运算量小得多,FFT充分利用了DFT运算中的对称性和周期性,从而将DFT运算量从N2减少到N*log2N。当N比较小时,FFT优势并不明显。但当N大于32开始,点数越大,FFT对运算量的改善越明显。比如当N为1024时,FFT的运算效率比DFT提高了100倍。