树形DP总结【acwing提高课】

树的最长路径

思路

基本想法就是dfs求出子树的最大高度

基于这个求出最大高度、次大高度

代码

#include
using namespace std;
const int N=2e4+100;
int h[N],ne[N],w[N],e[N],idx;
void add(int a,int b,int c)
{
     
    e[idx]=b;
    ne[idx]=h[a];
    w[idx]=c;
    h[a]=idx++;
}
int n,m;
int res=0;
int dfs(int u,int fa)
{
     
    int maxv=0;
    int d1=0,d2=0;
    for(int i=h[u];~i;i=ne[i])
    {
     
        int j=e[i];
        if(j==fa) continue;
        int d=dfs(j,u)+w[i];
        maxv=max(maxv,d);
        if(d>d1){
        //注意这里的更新
            d2=d1;
            d1=d;
        }
        else if(d>d2)
            d2=d;
    }
    res=max(d1+d2,res);
    return maxv;
}
int main()
{
     
    cin>>n;
    memset(h,-1,sizeof h);
    for(int i=1;i<n;i++)
    {
     
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
        add(b,a,c);
    }
    dfs(1,-1);
    cout<<res<<endl;
    //cout<
    return 0;
}

树的中心

思路

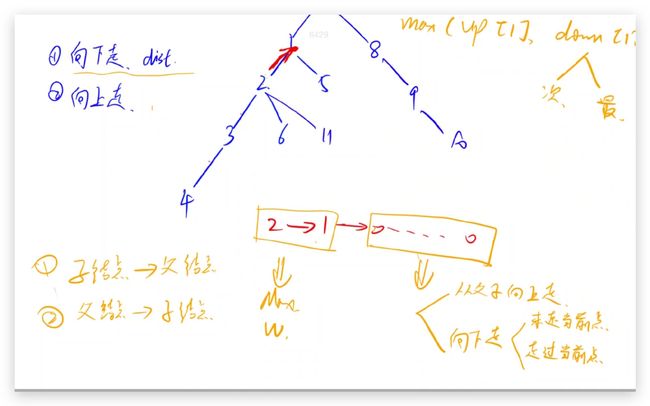
每个点分为向上走、向下走

向下走的最大值，简单的dfs

向上走，用父节点更新子节点，当父节点的d1经过子节点，子节点向上走，然后取（up[u],d2[u]+w)

不经过子节点，子节点向上走，然后取（up[u] , d1[u]+w)

考虑怎么判断是不是经过这个节点，开一个变量p1【】

代码

#include
using namespace std;
const int N=2e4+10;
int h[N],ne[N],w[N],e[N],idx;
void add(int a,int b,int c)
{
     
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}
int p1[N],d1[N],d2[N],n,up[N];
bool is_l[N];
int dfs_d(int u,int fa)
{
     
    int dist=-0x3f3f3f3f;
    d1[u]=d2[u]=-0x3f3f3f3f;
    for(int i=h[u];~i;i=ne[i])
    {
     
        int j=e[i];
        if(j==fa) continue;
        int d=dfs_d(j,u)+w[i];
        dist=max(dist,d);
        if(d>=d1[u])
        {
     
            d2[u]=d1[u],d1[u]=d;
            p1[u]=j;
            
        }
        else if(d>d2[u]) d2[u]=d;
    }
    if(d1[u]==-0x3f3f3f3f)
    {
     
        d1[u]=d2[u]=dist=0;
        is_l[u]=1;
    }
    return dist;
}
void dfs_u(int u,int fa)
{
     
    for(int i=h[u];~i;i=ne[i])
    {
     
        int j=e[i];
        if(j==fa) continue;
        if(j==p1[u]) up[j]=max(up[u],d2[u])+w[i];
        else{
     
            up[j]=max(up[u],d1[u])+w[i];
        }
        dfs_u(j,u);
    }
}
int main()
{
     
    cin>>n;
    memset(h,-1,sizeof h);
    for(int i=1;i<n;i++)
    {
     
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c),add(b,a,c);
    }
    dfs_d(1,-1);
    dfs_u(1,-1);
    int res=d1[1];
    for(int i=2;i<=n;i++)
    {
     
        if(is_l[i]) res=min(res,up[i]);
        else res=min(res,max(up[i],d1[i]));
    }
    cout<<res<<endl;
}

数字转化

题意

思路

转化条件，可以换为在一个树上最长路径

怎么建立这个树

某个数的约数和小于这个数，求这个数的约数和，直接求约数和，复杂度有点高，考虑求倍数

枚举每个数的倍数，从2倍开始枚举,这个数的倍数加这个数，可以方便的求约数和

for(int i=1;i<=n;i++)
{
     
        for(int j=2;j*i<=n;j++)
            sum[i*j]+=i;
}

在sum里面判断条件之后，建树，然后求最长路径

#include
using namespace std;
const int N=1e6;
int sum[N],n,h[N],ne[N],e[N],w[N],idx;
void add(int a,int b)
{
     
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}
int ans;
int dfs(int u)
{
     
    int dist=0;
    int d1=0,d2=0;
    for(int i=h[u];~i;i=ne[i])
    {
     
        int j=e[i];
        int d=dfs(j)+1;
        dist=max(dist,d);
        if(d>=d1) d2=d1,d1=d;
        else if(d>d2) d2=d;
        ans=max(ans,d1+d2);
    }
    return dist;
}
int main()
{
     
    cin>>n;
    memset(h,-1,sizeof h);
    for(int i=1;i<=n;i++)
    {
     
        for(int j=2;j*i<=n;j++)
            sum[i*j]+=i;
    }
    for(int i=1;i<=n;i++)
        if(sum[i]<i)
        {
     
            add(sum[i],i);
        }
    dfs(1);
    cout<<ans<<endl;
}

二叉苹果树

题意

要保留与根连接的树枝，求权重最大值

思路

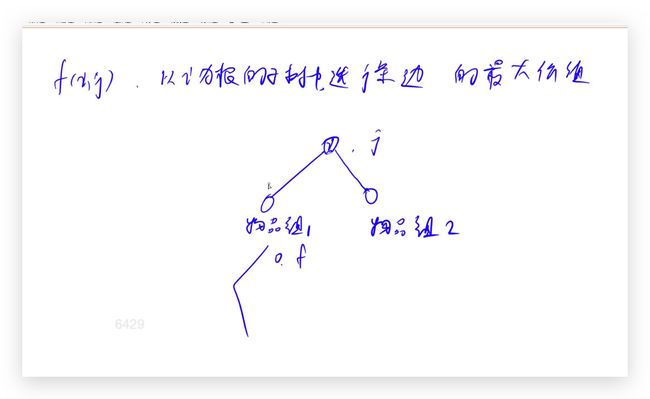
有依赖背包问题的化简版

状态表示：f[i] [j] :以i为节点，共j个树枝的最大值

状态转移：按照分组背包的方式，需要注意边数的变化

战略游戏

题意

树上的边最少选择一个点，求选择点的最少数

代码

#include
using namespace std;
const int N=2e4;
int n,f[N][2],ne[N],e[N],h[N],idx;
int st[N];
void add(int a,int b)
{
     
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}
void dfs(int u)
{
     
    f[u][0]=0;
    f[u][1]=1;
    for(int i=h[u];~i;i=ne[i])
    {
     
        int j=e[i];
        dfs(j);
        f[u][0]+=f[j][1];
        f[u][1]+=min(f[j][1],f[j][0]);
    }
}
int main()
{
     
    while(scanf("%d",&n)==1)
    {
     
        memset(h,-1,sizeof h);
        idx=0;
        memset(st,0,sizeof st);
        for(int i=0;i<n;i++)
        {
     
            int id,cnt;
            scanf("%d:(%d)",&id,&cnt);
            while(cnt--)
            {
     
                int b;
                cin>>b;
                add(id,b);
                st[b]=1;
            }
        }
        int root=0;
        for(int i=0;i<n;i++) 
            if(st[i]==0) 
                root=i;
       // cout<
       
        cout<<min(f[root][0],f[root][1])<<endl;
    }
}

皇宫看守

题意

树中一个点就可以看到其他直接相邻的点，求最少位置

类似状态机：每个点有3种情况：自己安排哨兵，被父节点哨兵看到，被子哨兵看到，3种状态。

0:表示被父节点看到

1:表示被子节点看到

2:表示在这个位置放

其中f（i,1) 可以优化一下

代码

#include
using namespace std;
const int N=3e3+10;
int h[N],ne[N],e[N],w[N],idx;
void add(int a,int b)
{
     
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}
int n;
int st[N];
int f[N][3];
void dfs(int u)
{
     
    f[u][2]=w[u];
    for(int i=h[u];~i;i=ne[i])
    {
     
        int j=e[i];
        dfs(j);
        f[u][0]+=min(f[j][1],f[j][2]);
        f[u][2]+=min(min(f[j][0],f[j][1]),f[j][2]);
    }
    f[u][1]=0x3f3f3f3f;
    for(int i=h[u];~i;i=ne[i])
    {
     
        int k=e[i];
        f[u][1]=min(f[u][1],f[u][0]-min(f[k][1],f[k][2])+f[k][2]);
    }
}
int main()
{
     
    cin>>n;
    memset(h,-1,sizeof h);
    for(int i=0;i<n;i++)
    {
     
        int id,cost,cnt;
        cin>>id>>cost>>cnt;
        w[id]=cost;
        while(cnt--)
        {
     
            int b;
            cin>>b;
            add(id,b);
            st[b]=1;
        }
    }
    int root=0;
    for(int i=1;i<=n;i++) 
        if(st[i]==0)
            root=i;
            
    dfs(root);
    cout<<min(f[root][1],f[root][2])<<endl;
}