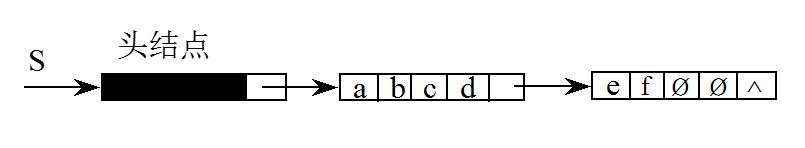数据结构(11)--串的模式匹配算法之BF、KMP算法

参考书籍：数据结构（C语言版）严蔚敏吴伟民编著清华大学出版社

本文中的代码可从这里下载：https://github.com/qingyujean/data-structure

1.串的存储

1.1定长顺序存储

串的定长顺序存储（静态数组）：

    #define  MAXSTRLEN  255  // 用户可在255以内定义最大串长

     typedef unsigned char  SString[MAXSTRLEN + 1];//0号单元存放串的长度

特点:
    串的实际长度可在这个预定义长度的范围内随意设定，超过预定义长度的串值则被舍去，称之为“截断” 。
    串长表示方法：

        一、下标0单元存串长
        二、在串值后面加一个不计入串长的结束标记字符。C语言中的串以一个‘\0’空字符为结束符，串长是一个隐含值。

1.2堆分配存储表示

 

串的堆分配存储表示（动态数组：malloc、realloc）:

typedef struct
 {
       char *ch;  // 若是非空串，则按串实际长度分配存储区，否则 ch 为NULL
        int  length;   // 串长度
} HString;

    通常，C语言中存在一个称之为“堆”的自由存储区，并由动态分配函数malloc( ) 和 free( ) 进行串值空间的动态管理。malloc函数为每个新产生的串分配一块实际串长所需的存储空间，若分配成功，则返回一个指向起始地址的指针，作为串的基址。

1.3块链存储表示

#define  CHUNKSIZE  80  // 可由用户定义的块大小
typedef  struct Chunk {  // 结点结构
    char  ch[CUNKSIZE];
    struct Chunk  *next;
} Chunk;
typedef struct {  // 串的链表结构
    Chunk *head, *tail; // 串的头和尾指针
     int   curlen;     // 串的当前长度
} LString;

    和紧缩存储类似，假设一个字中可以存储K个字符，则一个结点有K个数据域和一个指针域，若一个结点中数据域少于K个，用ø代替。例如，串S=‘abcdef’的存储结构具体形式如下图所示。假设K=4，并且链表带头结点。

    

2.串的模式匹配算法

下面的算法均以定长顺序结构表示串。

2.1BF算法

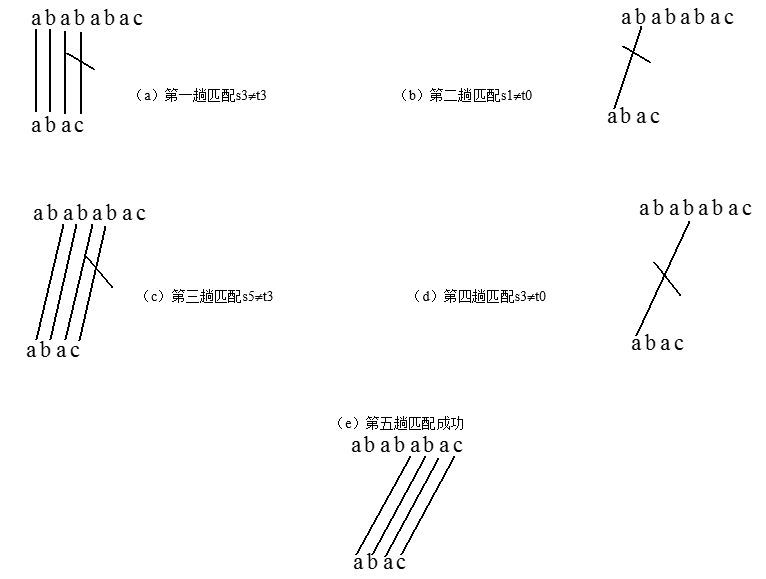
算法的基本思想：从主串的第1个字符起和模式串的第一个字符比较，若相等，则继续逐个比较后续字符，否则从主串的第2字符起重新和模式串的字符比较。依次类推，直到模式串t中的每个字符依次和主串s中的一个连续的字符序列相等，则匹配成功。否则匹配不成功。

模式匹配过程如下图所示，假设S=‘abababac’，T=“abac”。

BF算法最好情况下的时间复杂度是O(n+m)，最坏情况下的时间复杂度是O(n*m)，但在一般情况下，其实际的执行时间近似于O(n+m)，因此至今仍被采用。

下面利用BF算法实现求字串位置的定位函数。

 

#include
//串的定长顺序存储表示
#define MAXSTRLEN 50  // // 用户可在50以内定义最大串长
typedef unsigned char SString[MAXSTRLEN + 1];//0号单元存放串的长度

//返回子串T在主串S中第pos个字符之后的位置。若不存在，则函数值为0。其中，T非空，1<=pos<=StrLength(S)。
int indexBF(SString S, SString T, int pos){
	int i = pos, j = 1;
	while(i <= S[0] && j <= T[0]){
		if(S[i] == T[j]){
			i++;
			j++;
		}else{
			i = i - j + 2;//i回到原位置是i - j + 1 ,所以i退到远位置的下一个位置是i - j + 1 + 1
			j = 1;
		}
	}
	if(j > T[0]){//如果j > len(T)，说明模式串T与S中某子串完全匹配
		return i - T[0];//因为i是已经自增过一次了，所以是i-len(T)而不是i-len(T)+1
	}else
		return 0;
}

void init(SString &S, char str[]){
	int i = 0;
	while(str[i]!='\0'){
		S[i+1] = str[i];
		i++;
	}
	S[i+1] = '\0';
	S[0] = i;
}

void printStr(SString Str){
	for(int i = 1; i <= Str[0]; i++){
		printf("%c", Str[i]);
	}
	printf("\n");
}
void main(){
	SString S ;
	init(S, "ababcabcacbab");
	printStr(S);

	SString T;
	init(T, "abcac");
	printStr(T);

	int index = indexBF(S, T, 1);
	printf("index is %d\n", index);
}

运行结果：

 

2.1KMP算法

    造成BF算法速度慢的原因是回溯，即在某趟的匹配过程失败后，对于s串要回到本趟开始字符的下一个字符，t串要回到第一个字符。而这些回溯并不是完全必要的。
    KMP算法的核心思想是利用已经得到的部分匹配信息来进行后面的匹配过程。在匹配过程中指针 i 没有回溯。

    某趟在si和tj匹配失败后，即当 S[i] <> T[j] 时，已经得到的结果:S[ i-j+1 ... i-1 ] == T[ 1 ... j-1 ]
    如果模式串中有满足下述关系的子串存在：T[ 1 ... k-1 ] == T[ j-k+1 ... j-1 ]
    则有       S[i-k+1..i-1] == T[1..k-1]
    即：模式中的前k-1个字符与模式中tj字符前面的k-1个字符相等时，模式t就可以向右"滑动"至使tk和si对准，继续向右进行比较即可。

匹配过程如下图：

重点：模式中的next函数：当匹配过程中“失配”时，模式串“向右滑动的距离多远”，换句话说，当主串中的第i个字符与模式中的第j个字符“失配时”，主串中第i个字符（i指针不回溯）此时应与模式中哪个字符比较。这个字符定义为j的next位置，即i对应的主串字符应与next[j]对应的模式字符继续比较。

    模式中的每一个tj都对应一个k值，这个k值仅依赖于模式T本身字符序列的构成，而与主串S无关。

例如下列串的next值情况如下：

利用next值进行匹配：

那么next值如何求得呢？

 

求 next 函数值的过程是一个递推过程，分析如下:

已知：next[1] = 0；

假设：next[j] = k;即

此时， next[j+1]=？有两种可能：

（1）若tk=tj,则有，

            则：next[j+1] = k+1 = next[j] + 1

（2）若tk!=tj,则有

            则需往前回朔，检查 tj = t？

这实际上也是一个匹配的过程，不同在于：主串和模式串是同一个串。

由于此时tk!=tj,相当于k指示的是模式，j指示的是主串，则此时应比较k的next值即next[k]对应的模式字符，设next[k]=k’, 即比较tk’与tj。若tk’ = tj，则next[j+1] = k’+1 = next[k’]+ 1；若tk’也不等于tj，则需再找tk’的next值，若设next[tk’] = k’’ ,则比较tk’’与tj，……，以此类推，直至tj与某个模式中某个字符匹配成功或者不存在任何k’（1

（1

这样可得到next算法如下：

void get_next(SString &T, int &next[] )
{   // 求模式串T的next函数值并存入数组next。
    i = 1;   next[1] = 0;   j = 0;
    while (i < T[0])
    {    if (j == 0 || T[i] == T[j])
             {++i;  ++j; next[i] = j; }
        else  j = next[j];
    }
} // get_next

分析上面的代码：

    1.当比较到主串第第i个字符与模式的第j个字符时，若si != tj而导致j退回到0，说明模式串的第一个字符就“失配”了，此时要从主串的第i+1个字符起，与模式的第1个字符开始重新比较，即next[i+1] = 1,所以j == 0 时，由于 i,j均自增了，则就是next[i] = j;

    2.当比较到主串第第i个字符与模式的第j个字符时，当si !=tj 时，则应比较si与t next[j]，因为设置了新j = next[j] ，则是比较si与新tj，若此时有si = tj，则next[i+1] = j+1，所以当i、j均自增后，应有next[i] = j。

    3.当比较到主串第第i个字符与模式的第j个字符时，当si !=tj 时，则应比较si与t next[j]，因为设置了新j‘ = next[j] ，则是比较si与新tj’，若此时新的tj‘ = 旧的tj，那么新的tj’ 也不会等于si，即需要继续寻找新的tj‘的next值--j'' = next[j']对应的字符tj''，即next[j'] = next[j''](前提：tj' = tj'')，

所以根据上述的第3点，我们可以更加修正上面的next算法，当ti = tj'时，如果ti+1 != tj'+1，则next[i+1]  = j'+1，否则若ti+1 = tj'+1，则next[i+1] = next[j'+1]。

    KMP算法的时间复杂度可以达到O(m+n)。BF算法最好情况下的时间复杂度是O(n+m)，最坏情况下的时间复杂度是O(n*m)，但在一般情况下，其实际的执行时间近似于O(n+m)，因此至今仍被采用。KMP算法仅当模式与主串之间存在许多“部分匹配”的情况下才显得比BF算法快得多。

kmp算法实现：

 

//求模式串T的next函数（修正方法）值并存入next数组
void getNextVal(SString T, int next[]){
	next[1] = 0;
	int i = 1, j = 0;
	while(i < T[0]){
		if(j == 0 || T[i] == T[j]){
			i++;  //继续比较后续字符
			j++;
			if(T[i] == T[j])//若除去if(T[i] == T[j])：next[i] = next[j];这2句，则得到的就是修正之前的next求解算法
				next[i] = next[j];
			else
				next[i] = j;
		}else{
			j = next[j];//模式串向右滑动
		}
	}	
}

//返回子串T在主串S中第pos个字符之后的位置。若不存在，则函数值为0。其中，T非空，1<=pos<=StrLength(S)。
int indexKMP(SString S, SString T, int pos, int next[]){
	int i = pos, j = 1;
	while(i <= S[0] && j <= T[0]){
		if(j == 0 || S[i] == T[j]){
			i++;  //继续比较后续字符
			j++;
		}else{
			j = next[j];//模式串向右滑动
		}
	}
	if(j > T[0]){//如果j > len(T)，说明模式串T与S中某子串完全匹配
		return i - T[0];//因为i是已经自增过一次了，所以是i-len(T)而不是i-len(T)+1
	}else
		return 0;
}

void main(){
	SString S ;
	init(S, "ababcabcacbab");
	printStr(S);

	SString T;
	init(T, "abcac");
	printStr(T);

	//int index = indexBF(S, T, 1);
	//printf("index is %d\n", index);

	int next[6] = {0};
	getNextVal(T, next);
	//打印next值
	printf("next[]：");
	for(int k = 1; k <= T[0]; k++)
		printf("%d ", next[k]);
	printf("\n");

	int index = indexKMP(S, T, 1, next);
	printf("index is %d\n", index);
}

运行结果：