tplink图像岗提前批笔试、面试

选择题

1.景深是由什么决定的

景深（DOF）是指照片中在对焦平面前后画面清晰的部分。大景深意味着照片无论远近静物大部分都是清晰的。小（或浅）景深意味着照片中只有一部分画面是清晰的，其他画面都被虚化掉了。

在焦点前后，光线开始聚集和扩散，点的影象变成模糊的，形成一个扩大的圆，这个圆就叫做弥散圆。如果弥散圆的直径小于人眼的鉴别能力，在一定范围内实际影象产生的模糊是不能辨认的。这个不能辨认的弥散圆就称为容许弥散圆。

影响景深的因素
(1).镜头光圈：
光圈越大，景深越小；光圈越小，景深越大；

(2).镜头焦距
镜头焦距越长，景深越小；焦距越短，景深越大；

(3).拍摄距离
距离越远，景深越大；距离越近，景深越小。

2. 256＊256的图像，若灰度级数为16，则存储它所需的比特数为：

16级灰度存储需要4bit。256*4 ＝ 1024
结果为256K

3. 图像的二阶导数滤波器（拉普拉斯）对噪声更敏感

图像的二阶导数比一阶导数获得的物体边界更加细致。但是，显而易见的，二阶导数对噪声点也更加敏感，会放大噪声的影响。

4.消除小的连通域用什么操作（开运算）

先腐蚀后膨胀的过程称为开运算。用来消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积。

先膨胀后腐蚀的过程称为闭运算。用来填充物体内细小空洞、连接邻近物体、平滑其边界的同时并不明显改变其面积。
详细参考链接 https://blog.csdn.net/caojinpei123/article/details/81916005

简答题

1. 高斯成像公式

1/f=1/u+1/v。其中f为焦距，凸正凹负；u为物距；v为像距

LBP，HOG等特征的可扩展性等性质

旋转缩放后是否变化

SVM

核函数作用

将特征映射到高维空间

核函数种类

高斯核、线性核、多项式核

核函数选择

软性SVM中C的作用和怎么调节

信号采样

人声频率范围是300-3200Hz，问不失真的最小采样频率

8KHz的采样频率下，采用8bit的PCM，存储一秒钟的信号数据量有多大

VGG网络的每层参数量分析

https://www.imooc.com/article/details/id/30565
计算量（时间复杂度）
参数量（空间复杂度）
我们以VGG-16的第一层卷积为例：输入图像224×224×3，输出224×224×64，卷积核大小3×3。
计算量：
Times≈224×224×3×3×3×64=8.7×107
参数量：
Space≈3×3×3×64=1728

神经网络调参效果不理想时怎么分析

编程题

中值滤波

根据题目条件，逐步找到g最大条件下的threshold

g＝w0w1(u0-u1)*(u0-u1)
w0为小于threshold i的像素点占所有像素的比重，u0为像素点灰度的均值
w1为大于threshold i的像素点占所有像素的比重，u1为像素点灰度的均值

面试提问

图像去噪方法

高斯滤波、中值滤波

边缘检测算子

sobel、canny、roberts、拉普拉斯算子

二面

模型压缩和加速的方法

https://mp.weixin.qq.com/s/320ndRkhsMmaCPLbJtRAaw
mobile net与其他网络的不同
MobileNet的95%的计算都花费在了1×1的卷积上

mobile net V1 2017

引入深度可分离卷积
深度可分离卷积 ＝ 深度卷积 ＋ 逐点卷积

问题1：有人在实际使用的时候， 发现深度卷积部分的卷积核比较容易训废掉：训完之后发现深度卷积训出来的卷积核有不少是空的。
原因：对低维度做ReLU运算，很容易造成信息的丢失。而在高维度进行ReLU运算的话，信息的丢失则会很少。

问题2: 如果来的通道很少的话，DW深度卷积只能在低维度上工作，这样效果并不会很好，所以我们要“扩张”通道。

V2

同时引入shortcut结构，像Resnet一样复用特征。

步长为1时，先进行1×1卷积升维，再进行深度卷积提取特征，再通过Linear的逐点卷积降维。将input与output相加，形成残差结构。步长为2时，因为input与output的尺寸不符，因此不添加shortcut结构，其余均一致。

V3 2019

0. 网络的架构基于NAS实现的MnasNet（效果比MobileNetV2好）
1. 引入MobileNetV1的深度可分离卷积
2. 引入MobileNetV2的具有线性瓶颈的倒残差结构
3. 引入基于squeeze and excitation结构的轻量级注意力模型(SE)
4. 使用了一种新的激活函数h-swish(x)

原swish函数：

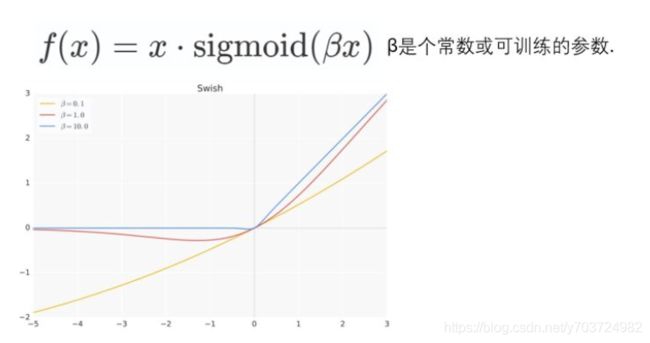
Swish具备无上界有下界、平滑、非单调的特性。并且Swish在深层模型上的效果优于ReLU。

问题：sigmoid()在移动设备上难以计算。
解决：h－swish(x)

能够将过滤器的数量减少到16个的同时保持与使用ReLU或swish的32个过滤器相同的精度，这节省了3毫秒的时间和1000万MAdds的计算量。

作者只在模型的后半部分使用h-swish。

5. 网络结构搜索中，结合两种技术：资源受限的NAS（platform-aware NAS）与NetAdapt

资源受限的NAS，用于在计算和参数量受限的前提下搜索网络来优化各个块（block），所以称之为模块级搜索（Block-wise Search） 。

NetAdapt，用于对各个模块确定之后网络层的微调每一层的卷积核数量，所以称之为层级搜索（Layer-wise Search）。

6. 修改了MobileNetV2网络端部最后阶段

将1×1层放在到最终平均池之后。这样的话最后一组特征现在不是7x7（下图V2结构红框），而是以1x1计算（下图V3结构黄框）。

在不会造成精度损失的同时，减少10ms耗时，提速15%，减小了30m的MAdd操作。

efficient net

SGD与Adam等优化器的不同

http://ruder.io/optimizing-gradient-descent/

1. Batch gradient descent
   根据整个数据集的数据计算参数的迭代更新。
   $$\theta =\theta -\eta \cdot {\nabla }_{\theta }J(\theta )$$
   缺点：1）慢 2）占用内存大 3）数据集中加入新图片

2. Stochastic(随机的) gradient descent
   根据每个训练数据 $x^{(i)}$ 和label $y^{(i)}$进行更新
   $$\theta =\theta -\eta \cdot {\nabla }_{\theta }J(\theta ;x^{(i)};y^{(i)})$$
   优点：1）快 2）可以在线学习new example
   缺点：波动大
   
   SGD’s fluctuation, on the one hand, enables it to jump to new and potentially better local minima. On the other hand, this ultimately complicates convergence to the exact minimum, as SGD will keep overshooting. However, it has been shown that when we slowly decrease the learning rate, SGD shows the same convergence behaviour as batch gradient descent, almost certainly converging to a local or the global minimum for non-convex and convex optimization respectively.

3. Mini-batch gradient descent
   根据每个batch中的n个训练数据进行更新
   $$\theta =\theta -\eta \cdot {\nabla }_{\theta }J(\theta ;x^{(i:i+n)};y^{(i:i+n)})$$
   优点：训练更稳定且足够快
   改进的SGD一般指的是mini-batch gradient descent

4. 挑战
   1）选择正确的学习率很困难
   2）训练中改变学习率的规则和threshold阈值要提前设定好，不能根据不同数据集智能调节。
   3）参数更新用的是同样的学习率（数据稀疏sparse或feature出现频率相差很大，prefer to perform a larger update for rarely occurring features.）
   4）优化非凸误差函数的另一个关键挑战是避免陷入其众多次优局部极小，以及鞍点。鞍点会让SGD陷入困境，因为各个维度上它的梯度都为0。

5. 动量 Momentum
   SGD很难在沟壑中导航，即表面在一个维度上的曲线比在另一个维度上的曲线陡得多的区域。在这些情况下，SGD在沟壑的斜坡上振荡，同时仅在底部朝着局部最佳状态缓慢前进，如图2所示。

   优点：有助于在相关方向上加速SGD并抑制振荡

   $v_t=\gamma v_{t-1}+\eta {\nabla }_{\theta }J(\theta )$
   $\theta =\theta -v_t$

   $\gamma$ 一般为0.9。

动量项增加了梯度指向相同方向的维度，并减少了梯度改变方向的维度的更新。因此，我们得到了更快的收敛和减少振荡。

6. Nesterov accelerated gradient (NAG)
   一个盲目地沿着斜坡滚下山的球是不够的。我们想要一个更聪明的球，它知道在山再次上坡之前减速。
   $v_t=\gamma v_{t-1}+\eta {\nabla }_{\theta }J(\theta -\gamma v_{t-1})$
   $\theta =\theta -v_t$

   基于参数未来的大致位置来更新而不是基于参数当前位置来更新。
   这种预期性的更新阻止了我们走得太快，从而提高了灵敏度，在RNN中取得了很好的效果。
   蓝线为momentum，绿线为NAG。
   
   现在，我们能够根据损失函数的斜率调整更新，并反过来加速SGD。我们还希望根据每个参数的重要性调整更新。

7. Adagrad 2010
   与频繁出现的feature相关的参数学习率较小；较少出现的feature相关的参数学习率较大。

   可用于训练word embedding模型，因为不经常使用的单词需要比经常使用的更新大得多。

$${\theta }_{t+1,i}={\theta }_{t,i}-\frac{\eta }{\sqrt{G_{t,ii}+ϵ}}\cdot g_{t,i}$$

Gt包括过去梯度的平方和。

Adagrad的主要好处之一是它消除了手动调整学习速度的需要。大多数初始学习率设为0.01。

问题：学习率会越来越小并趋于0。

8. Adadelta（自适应学习率调整）2012
   adadelta将累积过去梯度的窗口限制为一定的固定大小w。
   $$E[g^2{]}_t=\gamma E[g^2{]}_{t-1}+(1-\gamma )g_t^2$$
   用E代替G。

   $RMS[\Delta \theta {]}_t=\sqrt{E[\Delta {\theta }^2{]}_t+ϵ}$

   $\Delta {\theta }_t=-\frac{RMS[\Delta \theta {]}_{t-1}}{RMS[g{]}_t}{g}_t$

   ${\theta }_{t+1}={\theta }_t+\Delta {\theta }_t$

优点：不需要设置学习率。AdaDelta在训练初期和中期，具有非常不错的加速效果。

问题：到训练后期，进入局部最小值雷区之后，AdaDelta就会反复在局部最小值附近抖动。

9. RMSprop
   $E[g^2{]}_t=0.9E[g^2{]}_{t-1}+0.1g_t^2$
   ${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{E[g^2{]}_t+ϵ}}{g}_t$
   初始学习率设为0.01

10. Adam（Adaptive Moment Estimation）
    存储m类似动量，存储v类似RMSprop
    $m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t$
    $v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$

    m用于估计mean，v用于估计uncentered variance。
    为消除数据初始化的bias:

    ${\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t}$
    ${\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t}$
    更新法则如下：
    $${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}{\hat{m}}_t$$

    0.9 for β1, 0.999 for β2, Adam在众多自适应算法中最受欢迎。Adam, finally, adds bias-correction and momentum to RMSprop. 
    

11. AdaMax
    将l2 norm拓展到lp norm，u代替v没有bias。
    $u_t=\max ({\beta }_2\cdot v_{t-1},|g_t|)$
    ${\theta }_{t+1}={\theta }_t-\frac{\eta }{u_t}{\hat{m}}_t$

12. AMSGrad
    Adam的问题：It has been observed that some minibatches provide large and informative gradients, but as these minibatches only occur rarely, exponential averaging diminishes their influence, which leads to poor convergence.
    解决：用max替换原来平方相加得到的v
    $v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$
    ${\hat{v}}_t=\text{max}({\hat{v}}_{t-1},v_t)$
    最终公式：
    $${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}{m}_t$$

在小数据集和CIFAR－10上比Adam效果好，但其他数据集上效果变差。

鞍点和loss surfuce contour情况下自适应学习率的方法效果更好。

13. 怎么选优化器
    1）输入数据稀疏：自适应优化器
    2）SGD通常可以找到一个最小值，但它可能比某些优化器需要更长的时间，更依赖于一个健壮的初始化和学习率更新计划，并且可能陷入鞍点而不是局部极小值。

14. 训练SGD的trick
    1）并行分布的SGD：用于稀疏数据（互不影响）
    2）shuffle：每个epoch之后打乱训练数据
    3）Curriculum Learning：sort训练数据，以逐步变难的顺序
    4）Batch norm：为了便于学习，我们通常通过用零均值和单位方差初始化参数的初始值来规范化参数的初始值。随着训练的进展，我们将参数更新到不同的程度，我们会失去这种标准化，这会减慢训练速度，并随着网络的深入而扩大变化。

    Batch norm通过将规范化作为模型体系结构的一部分，我们可以使用更高的学习率，对初始化参数更鲁棒。批量规范化减少（有时甚至消除）Dropout的需要。
    5）early stop
    6）gradient noise

为什么参数的随机初始化比全0初始化好

1. 用普通SGD训练时，同样的loss对每一层的反馈一样，没有区分性。
2. 在逼近不同的局部最优点的时候，全0初始化只有一个固定的初始化点，不一定能找到合适的局部最优。随机初始化提供了更多可能性。