误报率、故障检测率、漏报率、虚警率、误警率等指标异同及计算公式
文章目录
- 误报率、故障检测率、漏报率、虚警率、误警率等指标异同及计算公式
-
- 1. 一些标准指标的计算
-
- true positive rate (tp rate)【真阳性率】, or hit rate 【命中率】, or recall 【召回率】:
- false positive rate (fp rate) 【假阳性率】, or false alarm rate:
- sensitivity【灵敏度】:
- specificity【特异度】:
- precision【精确度】:
- accuracy【准确度】:
- F measure【F值】:
- 2. 在化工等领域的故障检测中相关指标计算
-
- 故障检测率(fault detection rate,FDR):
- 故障L的故障检测率
- 误报率(false alarm rate,FAR)、虚警率、误检率:
- 漏报率(missing alarm rate,MAR)、漏检率、漏警率:
- 故障L的漏报率:
- 3. 在化工等领域的故障检测中哪个指标说法更专业?
-
- 误报率、故障检测率、false alarm rate、fault detection rate
- 4. 上述论述得到的结论
-
- 在 故障定义为阳性,正常定义为阴性 的前提下。
- 结论① 故障检测率=真阳性率=召回率
- 结论② 误报率=假阳性率
- 结论③ false alarm rate=误报率=虚警率=误检率等名称(纯粹是翻译不同)
- 结论④ missing alarm rate=漏报率=漏警率=漏检率等名称
- 结论⑤ 漏报率+故障检测率=1
- 结论⑥ 在化工等领域的故障检测中,用“误报率(false alarm rate)、故障检测率(fault detection rate)”是比较通用、比较专业的说法。
误报率、故障检测率、漏报率、虚警率、误警率等指标异同及计算公式
1. 一些标准指标的计算
参考论文:Fawcett T. An introduction to ROC analysis[J]. Pattern Recognition Letters, 2006, 27(8): 861–874.
谷歌学术显示这篇文章引用量有一万四千多,应该是比较权威经典的。
下面这部分相关指标的定义是从该论文中摘抄出来的
中括号【】内的【中文】,是自己根据相应英文含义加的
| True class 【真实类别】 | True class 【真实类别】 | ||
|---|---|---|---|
| p 【阳性】 | n 【阴性】 | ||
| Hypothesized class 【预测类别】 | Y 【阳性】 | TP(True Positives) 【真阳性】 | FP(False Positives) 【假阳性】 |
| Hypothesized class 【预测类别】 | N 【阴性】 | FN(False Negatives) 【假阴性】 | TN(True Negatives) 【真阴性】 |
注:Hypothesized class直接翻译好像是“被假定的类别”,不太清楚是什么意思,个人认为应该是指“预测类别”。
true positive rate (tp rate)【真阳性率】, or hit rate 【命中率】, or recall 【召回率】:
tp rate = T P T P + F N ≈ Positives correctly classified 【被正确分类的阳性数目】 Total positives 【总阳性数目】 \textrm{tp rate}=\frac{TP}{TP+FN}\approx\frac{\textrm{Positives correctly classified 【被正确分类的阳性数目】 }}{\textrm{Total positives 【总阳性数目】 }} tp rate=TP+FNTP≈Total positives 【总阳性数目】 Positives correctly classified 【被正确分类的阳性数目】
注:关于上面是约等号的问题,首先,原文说的是用后面这部分的公式去估计tp rate,个人想法是,前面的计算公式是理论公式,后面公式是用实验的结果来估计的意思吧。
false positive rate (fp rate) 【假阳性率】, or false alarm rate:
fp rate = F P F P + T N ≈ Negatives incorrectly classified【被错误分类的阴性数目】 Total negatives【总阴性数目】 \textrm{fp rate}=\frac{FP}{FP+TN}\approx\frac{\textrm{Negatives incorrectly classified【被错误分类的阴性数目】}}{\textrm{Total negatives【总阴性数目】}} fp rate=FP+TNFP≈Total negatives【总阴性数目】Negatives incorrectly classified【被错误分类的阴性数目】
sensitivity【灵敏度】:
sensitivity=recall \textrm{sensitivity=recall} sensitivity=recall
specificity【特异度】:
specificity = True negatives【真阴性】 False positives【假阳性】+True negatives【真阴性】 = 1 − fp rate \textrm{specificity}=\frac{\textrm{True negatives【真阴性】 }}{\textrm{False positives【假阳性】+True negatives【真阴性】}}=1-\textrm{fp rate} specificity=False positives【假阳性】+True negatives【真阴性】True negatives【真阴性】 =1−fp rate
precision【精确度】:
precision = T P T P + F P \textrm{precision}=\frac{TP}{TP+FP} precision=TP+FPTP
accuracy【准确度】:
accuracy = T P + T N T P + F N + T N + F P \textrm{ accuracy}=\frac{TP+TN}{TP+FN+TN+FP} accuracy=TP+FN+TN+FPTP+TN
F measure【F值】:
F measure = 2 1 precision + 1 recall \textrm{ F measure}=\frac{2}{\frac{1}{\textrm{precision}}+\frac{1}{\textrm{recall}}} F measure=precision1+recall12
2. 在化工等领域的故障检测中相关指标计算
以下是个人的理解,没有特意参照某篇论文,如有不同意见或错误,欢迎指出。
在故障检测里,因为只是故障检测,并不会区分故障1或者故障2,而是统统当成故障这一类别。
所以,将故障定义为阳性P,正常定义为阴性N,例如,故障1是阳性P,故障2也是阳性P。
那么故障检测中,常用的相关指标定义如下:
故障检测率(fault detection rate,FDR):
FDR = 被正确检测的故障(即故障被成功预测成故障)数目 故障总数目 = T P T P + F N = tp rate \textrm{FDR}=\frac{\textrm{被正确检测的故障(即故障被成功预测成故障)数目 }}{\textrm{故障总数目}}=\frac{TP}{TP+FN}=\textrm{tp rate} FDR=故障总数目被正确检测的故障(即故障被成功预测成故障)数目 =TP+FNTP=tp rate
因此,故障检测率与召回率、真阳性率是同一个计算公式,同一个含义。
故障L的故障检测率
故障L故障检测率 = 被正确检测的故障L(即故障L被成功预测成故障)总数 故障L总数目 \textrm{故障L故障检测率 }=\frac{\textrm{被正确检测的故障L(即故障L被成功预测成故障)总数 }}{\textrm{故障L总数目}} 故障L故障检测率 =故障L总数目被正确检测的故障L(即故障L被成功预测成故障)总数
其中,L是具体某类故障的标签。因此论文中,谈到“不同故障检测率”,用的是故障L的故障检测率公式。而“平均故障检测率”就是在不区分故障几的情况下计算的结果,即用的FDR或tp rate计算。
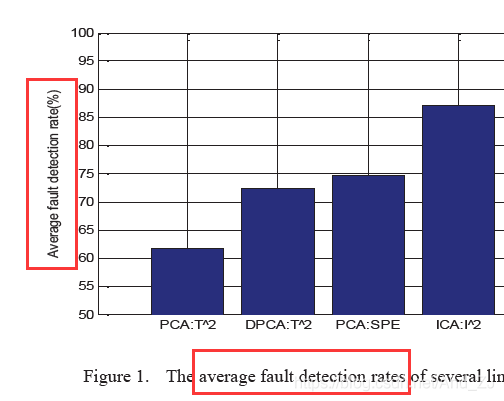
所以,如果在“fault detection rate”的讨论环境中,存在着不同故障,那用的是故障L的故障检测率公式。如果没有区分故障,那么指的就是原来的含义,不过,为了说明的更清楚,一般采用“average fault detection rate”,即平均故障检测率,所以,这样也算是作了相应的区分了。
论文示例 1:
来源:Lv F, Wen C, Bao Z, et al. Fault diagnosis based on deep learning[C]. 2016 American Control Conference (ACC). Boston, MA, USA: IEEE, 2016: 6851–6856.
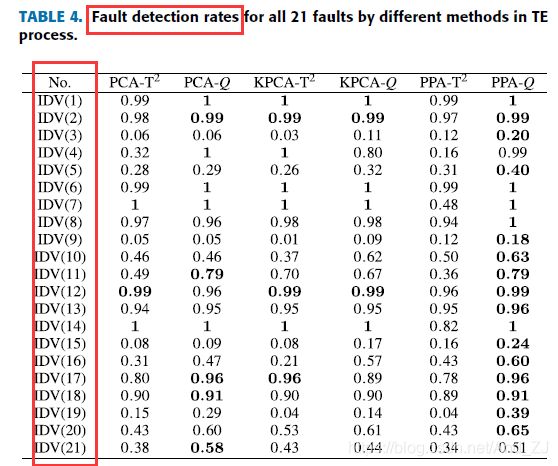
论文示例 2:
来源:Zhang X, Kano M, Li Y. Principal Polynomial Analysis for Fault Detection and Diagnosis of Industrial Processes[J]. IEEE Access, 2018, 6: 52298–52307.
这个讨论的是各故障的检测率,用的是故障L的故障检测率公式,左边第一列是21种故障:
误报率(false alarm rate,FAR)、虚警率、误检率:
FAR = 误报成故障的正常样本数目 正常总数目 = F P F P + T N = fp rate \textrm{FAR}=\frac{\textrm{误报成故障的正常样本数目}}{\textrm{正常总数目}}=\frac{FP}{FP+TN}=\textrm{fp rate} FAR=正常总数目误报成故障的正常样本数目=FP+TNFP=fp rate
误报的含义肯定是指正常被误报成故障(真实类别为正常,预测类别为故障),显然不会有故障误报成正常这一说法,只有故障漏报成正常的说法。
因此,误报率是与假阳性率同一个计算公式,同一个含义。
关于虚警率这个指标的问题,个人认为,完全是翻译的问题。
毕竟,false alarm rate 这个词,字面意思,假的警报比率,翻译成“误报率”、“虚警率”都是合理的翻译,甚至翻译成“误警率”,“虚报率”字面意思好像也完全说的通的,只是可能没有人这么说。
在百度翻译中,“虚警率”甚至被翻译成了“false positive rate”,即“假阳性率”了(而上面公式表明误报率和假阳性率确实是一样的)。
而在谷歌翻译中,“虚警率”被翻译成“false alarm rate”,而“false alarm rate”再翻译回中文时又成“误报率”了。
个人猜测,会不会是不同领域的故障检测的研究人员,由于侧重点不同或者什么原因,在翻译“false alarm rate”时,分别翻译成了“误报率”、“虚警率”、“误检率”之类的名称了,所以导致存在不同的翻译名称,但计算公式和含义是完全一样的。
漏报率(missing alarm rate,MAR)、漏检率、漏警率:
MAR = 漏报为正常的故障数目 故障总数目 = F N T P + F N \textrm{MAR}=\frac{\textrm{漏报为正常的故障数目}}{\textrm{故障总数目}}=\frac{FN}{TP+FN} MAR=故障总数目漏报为正常的故障数目=TP+FNFN
个人认为,漏报率、漏检率、漏警率等也是不同领域的翻译问题,它们其实是一样的。
故障L的漏报率:
故障L漏报率 = 漏报为正常的故障L数目 故障L总数目 \textrm{故障L漏报率}=\frac{\textrm{漏报为正常的故障L数目}}{\textrm{故障L总数目}} 故障L漏报率=故障L总数目漏报为正常的故障L数目
因此漏报率也可以分成“平均故障漏报率”和“故障L漏报率”。不过好像没见过用“平均故障漏报率”这一说法的。
漏报率这一指标,在使用时,存在和检测率一样的使用规则。
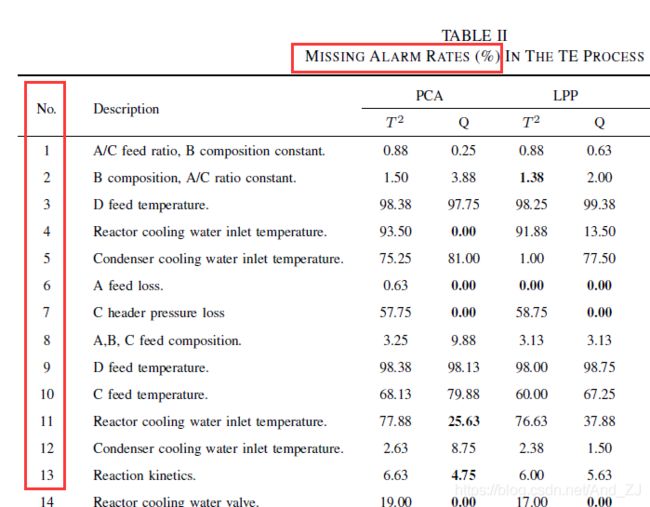
论文示例 3:
来源:Shi L, Tong C, Lan T, 等. Statistical process monitoring based on ensemble structure analysis[J]. IEEE/CAA Journal of Automatica Sinica, 2018: 1–8.
显然,这个漏报率+故障检测率=1,或者说平均漏报率+平均故障检测率=1,再或者说故障L漏报率+故障L故障检测率=1
因为和为1,所以,用故障检测率,一般就不用漏报率,反之亦然。
而“精确度”、“准确率”、“错误率”这类指标,在故障检测上一般没见使用,可能是这类指标会受到不同类别数目的影响,所以,在该领域讨论意义不大。
3. 在化工等领域的故障检测中哪个指标说法更专业?
误报率、故障检测率、false alarm rate、fault detection rate
阅读了一些该领域中的中英文论文,包括国内的硕博论文。
中文论文中,大家基本都是用的误报率、故障检测率这两个指标。用漏报率的比较少。用“虚警率”这类说法的几乎没有看到过。
个别人用了故障准确率等类似的说法,但是个人认为这一说法并不好,不知道什么意思,容易有歧义,也没看到它的计算公式,通过文章上下文,个人猜测,大概是故障检测率的意思吧。
英文论文中,一般都是用false alarm rate、fault detection rate,用missing alarm rate也有,但比较少见。
所以,个人认为,在化工过程的故障检测中,用误报率、故障检测率比用“虚警率、漏警率”更专业些。如有需要,不用故障检测率,用漏报率也是可以的。