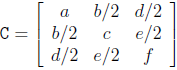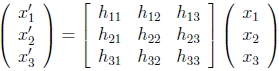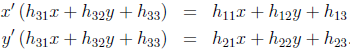平面的投影变换(1)——什么是投影变换?
1. 欧式几何、投影几何和投影变换
研究平面投影变换的任务是对一个平面在透视摄像机上成像时产生的几何畸变进行建模。
什么是投影变换?当我们看一张照片时,会发现物体的真实形状在相片中发生了变化,正方形不再是正方形了,圆形不再是圆形了。这就是投影变换造成的。
在一个平面的透视成像过程中,平面的某些几何属性被保留,某些则未保留。例如,一条直线成像后仍为直线(共线性),而原本平行的两条直线在成像后通常变为不平行了。那么,哪些几何属性会在投影变换中保留,那些不被保留呢?通常,平面的形状不会保留,例如正圆在投影后会变为椭圆,另外,角度、距离、距离比,等等,都不会保留。唯一能保留的几何属性似乎只有直线的共线性。
在欧式几何中,如果说在一个平面中任意两条直线必然相交于一点,是不能成立的,因为存在一个例外,即两条直线可以是平行的。这是欧式几何的麻烦之处。而换个说法,可以说平行的两条直线仍然相交于一点,只是它们相交于无限远处。这个在无限远处的交点,叫做理想点(ideal points)。由于增加了“理想点”,我们将传统的欧式空间拓展到了投影空间。在投影空间中,平面上任意两条直线的确是必然相交于一点的。
2. 投影空间和齐次(homogeneous)坐标
直线的齐次表示。平面R2中的一条直线用方程表示为ax+by+c=0,因此可以用向量(a,b,c)T来表示。注意向量(a,b,c)T和k(a,b,c)T表示同一条直线,或说是等价的。具有这种等价关系的一类向量叫做齐次向量。空间R3-(0,0,0)T中的一类等价向量构成投影空间P2,其中-(0,0,0)T表示该向量除外。注意,二维平面R2上的任一直线用三维向量表示,但该直线却是属于二维投影空间P2。
点的齐次表示。对于直线l=(a,b,c)T上的一点(x, y)T,有ax+by+c=0,写成向量内积的形式为(x, y,1) (a,b,c)T= (x, y,1)l = 0。其中(x, y,1)T就是点(x, y)T的齐次向量表示形式。点的任意齐次向量表示为(x1, x2, x3)T ,代表平面R2上的一点(x1/x3, x2/x3 )T ,其中前者为该点的齐次坐标,后者为非齐次坐标。以齐次向量表示的点也是投影空间P2的元素。
定理1:点x落于直线l上,当且仅当xTl = 0.
定理2:两条直线l和l′ 相交于点x = l × l′。其中×表示向量的叉积。
定理3:经过两点x和x' 连成一线l = x × x'。
3. 理想点和无穷线
平行直线的交点。两条平行直线的齐次表达式分别为l = (a,b,c)T和l' = (a,b,c')T,则由定理2,它们的交点为l × l' =(c' - c)(b, -a , 0)T,其最后一个坐标为0,对应于一个无限远处的点,叫做理想点。所有理想点的集合,(x1, x2, 0)T ,位于一条直线上,叫做无穷线,记作 l∞ =(0,0, 1)T。
经验证,理想点与无穷线的内积为(0, 0, 1)(x1, x2, 0)T = 0。
由定理2,直线l = (a,b,c)T与l∞相交于理想点(b, -a , 0)T,l 的平行线l' = (a,b,c')T与l∞相交于同一个理想点(b, -a , 0)T。而二维非齐次坐标(b, -a )T代表直线的方向,这意味着,理想点的位置沿l∞随直线的方向而变。因此,无穷线可被认为是平面上直线方向的集合。
这是投影几何与欧式几何的区别。在投影空间P2中,可以无条件地说两线必交于一点,两点必连成一线。而在欧式空间R2中,平行线是个例外。
投影平面模型。二维投影空间P2可以看做三维实数空间R3上的一组射线组成的集合。可以验证,两个不等的射线共同决定一个平面,两个平面相交于一个射线。正如同两点决定一条直线,两条直线相交于一点。
定理4(对偶定理): 对于2维投影几何中的任何定理,交换点、线的位置,得到的对偶定理也成立。
例如定理2和4就是一对对偶定理,即两点通过一线<=> 两线通过一点。
4. 二次曲线(conics)和对偶二次曲线(dual conics)
Conics是在平面中可用二次方程描述的一类曲线。在欧式几何中,conics包括三类(不包括非退行二次曲线):
- 双曲线(hyperbola)
- 椭圆(ellips)
- 抛物线(parabola)
而在2D投影几何中,这三类非退行二次曲线是等价的。
二次曲线在非齐次坐标中的方程为ax2 +bxy +cy2 + dx +ey +f = 0. 对它进行齐次化,即x→x1/x3, y→x2/x3,则得到
ax12 + bx1x2+ cx22 + dx1 x3 + ex2 x3 + f x32 = 0
写为矩阵形式:
xTCx = 0
其中C为二次曲线系数矩阵,
如点和线的齐次表示形式一样,在C中重要的是元素之间的比例。因此C就是二次曲线的齐次表达式。二次曲线有5个自由度。
一个conic可由5个点完全决定。将一个conic表示为一个6元向量c=(a,b,c,d,e,f)T,则由5个点得到
可见conic系数c是一个5×6矩阵的零向量,说明一个二次曲线由5个点决定。
定理5(conics切线定理): 直线 l = Cx 正切C于点x.
证明:对于直线 l = Cx,因为lTx = xTCx = 0,故 l 通过点x.
若 l 与C有另外一个交点y,则有yTCy = lTy = 0.
故对任一α,有 (x+αy)TC(x+αy) = 0.
这意味着,连接x和y的直线 l 上的任意一点都落在二次曲线C上,除非C是退行的。
对偶二次曲线(dual conics)。上面定义二次曲线C可以叫做点二次曲线,因为它定义在关于点的方程上。利用投影空间P2上的对偶定理,可以将二次曲线定义成关于线的方程,叫做线二次曲线,或对偶二次曲线,记作C*。C的切线 l 满足lTC*l = 0.
由conics切线定理,与C切于点x的切线为 l = Cx,若C满秩,则 x = C-1l,由xTCx = 0,得到(C-1l)TC(C-1l) =lTC-Tl = 0。考虑到C阵对称,故有lTC-1l = 0。因此在比例上有C* = C-1,可见C*是C的伴随矩阵。
此外,如果C不满秩,则变为退化二次曲线(degenerate conics)。
5. 投影变换
Felix Klein在他的名著 "Erlangen Program" [Klein-39]中认为,几何学是对变换中不变属性的研究。按照这一观点,2D投影几何研究的是投影空间P2在投影变换中的不变属性。
定义(投影):投影是在空间P2上的可逆映射h,在这个映射中,三个点x1, x2, x3位于同一条直线,当且仅当h(x1),h(x2),h(x3)也位于同一条直线。
投影也叫共射变换(collineation),投影变换,或单应性变换(homography)。
定理(投影变换定理):对于一个投影 h : P2→P2 ,一定存在一个非奇异3×3矩阵H,使得对任何P2上的齐次点x,有h(x) = Hx.
证明:给定直线l 上的三个点x1, x2, x3,则对于 i = 1,...,3,有lTxi = 0. 设H是一个非奇异3×3矩阵,则 lTH-1Hxi = 0,故所有的点Hxi 一定落在直线H-1l 上,在变换中保持了共线属性。
这个定理说明在齐次坐标系上的任何可逆的线性变换都是一个投影。
定义(投影变换):平面投影变换是对齐次3元向量的线性变换,它由一个非奇异3×3矩阵表示。
或简记为x' =Hx。其中H称为齐次矩阵,因为对它乘上一个任意非零系数不会影响投影变换的结果。这个投影变换有8个自由度。
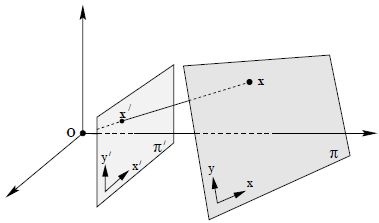
平面映射。沿着通过一个共同点(投影中心)的射线进行投影,则将一个平面映射为另一个平面。如果在每个平面中定义一个坐标系,则中心投影映射可以表示为x' = Hx。这种投影叫做透视,而不是一个全投影,它只有6个自由度。
从平面的透视图像中去除投影畸变。一个平面的中心投影成像是对原始平面进行投影变换生成的,而这种透视成像会造成形状畸变,通常在一个平面上的平行线成像后不再平行,而是相交于一个有限点。通过对成像进行反变换,可以去除投影畸变。方法是,首先通过点对点匹配计算投影变换,然后对得到的投影变换矩阵求逆。
设一对匹配点x和x'的非齐次坐标分别为(x,y)和(x',y' ),则投影变换可写为如下非齐次形式:
每一对匹配点产生两个关于H的元素的方程式:
若有4对匹配点,就可以产生8个关于H的元素的线性方程组,从而H可解(带一个无关紧要的因子)。
6. 直线和二次曲线的变换
直线的变换。相对于点变换x' = Hx,直线的变换是l' = H-Tl。对于直线l 上的一点xi,变换后l'Txi' = lTH-1Hxi = 0. 因此共线特性在变换中得以保留。注意,点变换针对H,线变换针对H-1,这是协变和逆变的区别。
二次曲线的变换。对于点变换x' = Hx,二次曲线方程写为xTCx = x'T[H-1]TCH-1x' = x'TH-TCH-1x',因此conic变换为
C'= H-TCH-1.
二次曲线变换是协变的。对偶二次曲线的变换为C*'= HC*HT.