A*算法的Matlab实现
A*算法的Matlab实现
- A*算法的Matlab实现
- 一、参考博客
- 二、代码如下:
- 1.pathfinding.m
- 2.AStar.m
- 3.FindList.m
- 4.GetBoundary.m
- 5.GetObstacle.m
- 6.GetPath
- 7.h.m
- 8.isObstacle
- 9.isopen
- 10.MotionModel
- 11.PlotGrid.m
- 12.FillPlot.m
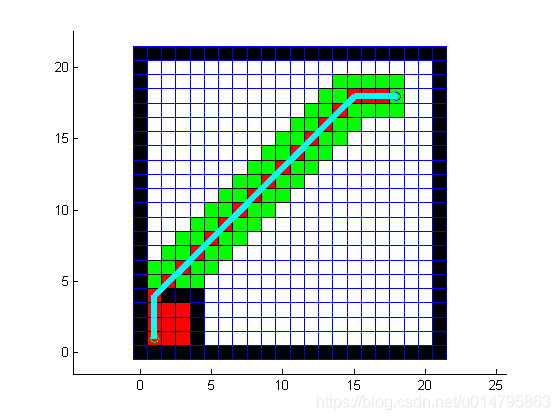
- 三、运行结果截图
A*算法的Matlab实现
一、参考博客
本文参考以下博客:
1.理解主要参考:
A*算法详解https://blog.csdn.net/m0_38054145/article/details/81808541
导航路径规划之五 A*算法https://blog.csdn.net/autonavi2012/article/details/80923431
2.代码主要参考:
手把手教用matlab做无人驾驶(三)-路径规划A*算https://blog.csdn.net/caokaifa/article/details/82314809
在之前的博客上修改的,重新改了画图函数!
二、代码如下:
注意:
1.以下代码是全部的代码,一个都没有少,大家可以直接复制运行;
2.程序运行时会动态绘制当前的close节点和open节点,直观展示寻路过程;
3.整个代码的注释还是挺详细的,理解起来应该没有问题的,我就不多加解释了;
4.代码打包下载:https://download.csdn.net/download/u014795863/11061995(现在的CSDN好像连资料下载所需积分都没法设置了,真是太差劲了,默认的是5分,不想下载可以直接复制下面的代码运行)。
1.pathfinding.m
起始角本文件,规定了障碍点,边界点,起点,终点及地图规模。
clear;
clc;
disp('A Star Path Planing start!!')
map.XYMAX=20; %%代表我们要画一个地图的长和宽
map.start=[1,1]; %起始点 注意必须在地图范围内
map.goal=[18,18]; %目标点 注意必须在地图范围内
obstacle=GetBoundary(map);%得到边界数据
nObstacle=0;%在地图中随机加入XX个障碍物
obstacle=GetObstacle(nObstacle,obstacle,map);%障碍物和边界坐标
obstacle = [obstacle;4,1; 4,2; 4,3; 4,4; 3,4 ;2,4;];%全封死的情况,是没有路的
%obstacle = [obstacle;1,2;2,1;2,2];%此也为全封死的情况,也没有路的
%obstacle = [obstacle;1,3;2,3;3,3;3,2;3,1];%此也为全封死情况,也没有路的
%
%load('obstacle1.mat');
%画出网格线
PlotGrid(map);
hold on;
%画出障碍点
FillPlot(obstacle,'k');
path=AStar(obstacle,map)%A*算法
%画出路径
%
if length(path)>=1
plot(path(:,1),path(:,2),'-c','LineWidth',5);hold on;
end
%}
2.AStar.m
整个Astar算法实现的核心代码,注释挺详细的,我就不多加解释了。
function path=AStar(obstacle,map)
%{
Astar算法思路
1.将起始点放在Openlist中
2.重复以下过程:
首先判断是否到达目标点,或无路径
>>如果终点已加入到Openlist中,则已找到路径(此时起始点就是目标点,无需再找)
>>Openlist为空,无路径
a.按照Openlist中的第三列(代价函数F)进行排序,查找F值最小的节点
b.把这个F值最小的节点移到Closelist中作为 当前节点
c.对当前节点周围的8个相邻节点:
>>如果它不可达,忽略它
>>如果它在Closelist中,忽略它
>>如果它不在Openlist中,加放Openlist,并把当前节点设置为它的父节点,记录该节点的F值
>>如果它已经在Openlist中,检查经当前节点到达那里是否更好(用G或F值判断),
>如果更好,则将当前节点设置为其父节点,并更新F,G值;如果不好,则不作处理
3.保存路径
%}
%用于存储路径
path=[];
%OpenList
open=[];
%CloseList
close=[];
%findFlag用于判断while循环是否结束
findFlag=false;
%================1.将起始点放在Openlist中======================
%open变量每一行 [节点坐标,代价值F=G+H,代价值G,父节点坐标]
open =[map.start(1), map.start(2) , 0+h(map.start,map.goal) , 0 , map.start(1) , map.start(2)];
%更新状态--下一步的八个点
next=MotionModel();
%=======================2.重复以下过程==============================
while ~findFlag
%--------------------首先判断是否达到目标点,或无路径-----
if isempty(open(:,1))
disp('No path to goal!!');
return;
end
%判断目标点是否出现在open列表中
[isopenFlag,Id]=isopen(map.goal,open);
if isopenFlag
disp('Find Goal!!');
close = [open(Id,:);close]
findFlag=true;
break;
end
%------------------a.按照Openlist中的第三列(代价函数F)进行排序,查找F值最小的节点
[Y,I] = sort(open(:,3)); %对OpenList中第三列排序
open=open(I,:);%open中第一行节点是F值最小的
%------------------b.将F值最小的节点(即open中第一行节点),放到close第一行(close是不断积压的),作为当前节点
close = [open(1,:);close];
current = open(1,:);
open(1,:)=[];%因为已经从open中移除了,所以第一列需要为空
%--------------------c.对当前节点周围的8个相邻节点,算法的主体:------------------------
for in=1:length(next(:,1))
%获得相邻节点的坐标,代价值F先等于0,代价值G先等于0 ,后面两个值是其父节点的坐标值,暂定为零(因为暂时还无法判断其父节点坐标是多少)
m=[current(1,1)+next(in,1) , current(1,2)+next(in,2) , 0 , 0 , 0 ,0];
m(4)=current(1,4)+next(in,3); % m(4) 相邻节点G值
m(3)=m(4)+h(m(1:2),map.goal);% m(3) 相邻节点F值
%>>如果它不可达,忽略它,处理下一个相邻节点 (注意,obstacle这个数组中是包括边界的)
if isObstacle(m,obstacle)
continue;
end
%flag == 1:相邻节点 在Closelist中 targetInd = close中行号
%flag == 2:相邻节点不在Openlist中 targetInd = []
%flag == 3:相邻节点 在Openlist中 targetInd = open中行号
[flag,targetInd]=FindList(m,open,close);
%>>如果它在Closelist中,忽略此相邻节点
if flag==1
continue;
%>>如果它不在Openlist中,加入Openlist,并把当前节点设置为它的父节点
elseif flag==2
m(5:6)=[current(1,1),current(1,2)];%将当前节点作为其父节点
open = [open;m];%将此相邻节点加放openlist中
%>>剩下的情况就是它在Openlist中,检查由当前节点到相邻节点是否更好,如果更好则将当前节点设置为其父节点,并更新F,G值;否则不操作
else
%由当前节点到达相邻节点更好(targetInd是此相邻节点在open中的行号 此行的第3列是代价函数F值)
if m(3) < open(targetInd,3)
%更好,则将此相邻节点的父节点设置为当前节点,否则不作处理
m(5:6)=[current(1,1),current(1,2)];%将当前节点作为其父节点
open(targetInd,:) = m;%将此相邻节点在Openlist中的数据更新
end
end
%下面的end是判断八个相邻节点的for循环的end
end
%=====绘制======
PlotGrid(map);
hold on;
pause(0.01);
%绘制节点close和open节点
FillPlot(close,'r');
hold on;
FillPlot(open,'g')
hold on;
end
%追溯路径
path=GetPath(close,map.start);
3.FindList.m
检查给定节点是否open列表中 是否在close列表中
function [flag,targetInd]=FindList(m,open,close)
%{
函数功能:
如果相邻节点(m存储其信息) 已经在Closelist中,则flag = 1 targetInd = 其所在close的行数,用来定位
如果相邻节点(m存储其信息) 不在Openlist 中,则flag = 2 targetInd = []
如果相邻节点(m存储其信息) 已经在Openlist 中,则flag = 3 targetInd = 其所在open的行数,用来定位
%}
%如果openlist为空,则一定不在openlist中
if isempty(open)
flag = 2;
targetInd = [];
else %open不为空时,需要检查是否在openlist中
%遍历openlist,检查是否在openlist中
for io = 1:length(open(:,1))
if isequal( m(1:2) , open(io,1:2) ) %在Openlist中
flag = 3;
targetInd = io;
return;
else %不在Openlist中
flag = 2;
targetInd = [];
end
end
end
%如果能到这一步,说明: 一定不在Openlist中 那么需要判断是否在closelist中
%遍历Closelist(注意closelist不可能为空)
for ic = 1:length(close(:,1))
if isequal( m(1:2) , close(ic,1:2) ) %在Closelist中
flag = 1;
targetInd = ic;
return;%在Closelist中直接return
end
end
%{
以下代码用于测试此函数的正确性:
open = [ 1,1 ; 2,2; 3,3; 4,4; 5,5; 6,6; 7,7; 8,8; 9,9];
%还有一种情况:open列表为空
close = [1,2 ; 2,3; 3,4; 4,5; 5,6; 6,7; 7,8];
m1 = [5,6]; %在close中 此时flag应为1 targetInd 应为 5
m2 = [0,0]; %不在open中, 此时flag应为2 targetInd 应为空[]
m3 = [3,3]; %在open中 此时flag应为3 targetInd 应为 3
[flag,targetInd] = FindList(m1,open,close) %flag = 1 targetInd = 5
[flag,targetInd] = FindList(m2,open,close) %flag = 2 targetInd = []
[flag,targetInd] = FindList(m3,open,close) %flag = 3 targetInd = 3
%}
end
4.GetBoundary.m
function boundary=GetBoundary(map)
%获得地图的边界的坐标
boundary=[];
for i1=0:(map.XYMAX+1)
boundary=[boundary;[0 i1]];
end
for i2=0:(map.XYMAX+1)
boundary=[boundary;[i2 0]];
end
for i3=0:(map.XYMAX+1)
boundary=[boundary;[map.XYMAX+1 i3]];
end
for i4=0:(map.XYMAX+1)
boundary=[boundary;[i4 map.XYMAX+1]];
end
end
5.GetObstacle.m
function obstacle=GetObstacle(nob,obstacle,map)
%生成障碍点的坐标
ob=round(rand([nob,2])*map.XYMAX);
%生成的障碍点有可能是和start点和goal点坐标重合的,需要删除,removeInd为重合点的数组索引index
removeInd=[];
%遍历ob数组,检查哪些坐标与start和goal重合,并将其索引存在removeInd中
for io=1:length(ob(:,1))
if(isequal(ob(io,:),map.start) || isequal(ob(io,:),map.goal))
removeInd=[removeInd;io];
end
end
%将重复的节点置空,去掉
ob(removeInd,:)=[];
%将ob障碍点加入到obstacle中(obstacle中已经包括边界节点的坐标了,这里还要再加上内部障碍点的坐标)
obstacle=[obstacle;ob];
6.GetPath
最后得到整个路径的坐标
function path=GetPath(close,start)
ind=1;
path=[];
while 1
path=[path; close(ind,1:2)];
if isequal(close(ind,1:2),start)
break;
end
for io=1:length(close(:,1))
if isequal(close(io,1:2),close(ind,5:6))
ind=io;
break;
end
end
end
end
7.h.m
启发函数的代价值,这里采用的是曼哈顿距离
function hcost = h( m,goal )
%计算启发函数代价值 ,这里采用曼哈顿算法
hcost =10* abs( m(1)-goal(1) )+10*abs( m(2)-goal(2) );
end
8.isObstacle
判断一个节点是否为障碍点(边界点也认为是障碍点)
function flag = isObstacle( m,obstacle )
%判断节点m是否为障碍点,如果是就返为1,不是就返回0
for io=1:length(obstacle(:,1))
if isequal(obstacle(io,:),m(1:2))
flag=true;
return;
end
end
flag=false;
end
9.isopen
判断一个节点是否在open列表中,感觉这个函数的功能和3中的FindList函数功能有些重复,但还是编了这个函数
function [isopenFlag,Id] = isopen( node,open )
%判断节点是否在open列表中,在open中,isopenFlag = 1,不在open中,isopenFlag = 0 .并反回索引号
isopenFlag = 0;
Id = 0;
%如果open列表为空,则不在open列表中
if isempty(open)
isopenFlag = 0;
else %open列表不为空时
for i = 1:length( open(:,1) )
if isequal( node(1:2) , open(i,1:2) ) %在Openlist中
isopenFlag = 1;
Id = i;
return;
end
end
end
end
10.MotionModel
得到当前节点周边的八个相邻节点的坐标差值和移动距离
function next = MotionModel()
%当前节点 周围的八个相邻节点 与 当前节点的坐标差值(前两列)
%当前节点 周围的八个相邻节点 与 当前节点的距离值(最后一列)
next = [-1,1,14;...
0,1,10;...
1,1,14;...
-1,0,10;...
1,0,10;...
-1,-1,14;...
0,-1,10;...
1,-1,14];
end
11.PlotGrid.m
绘制
function PlotGrid( map )
%PLOTGRID Summary of this function goes here
% Detailed explanation goes here
%绘制网格
for i = 1:map.XYMAX+3
line([-0.5,map.XYMAX+1.5],[i-1.5,i-1.5]);
end
for j = 1:map.XYMAX+3
line([j-1.5,j-1.5],[-0.5,map.XYMAX+1.5]);
end
hold on;
plot(map.start(1),map.start(2),'og');
hold on;
plot(map.goal(1),map.goal(2),'ob');
axis([-1.5,map.XYMAX+2.5,-1.5,map.XYMAX+2.5]);
axis equal;
end
12.FillPlot.m
function FillPlot(coord,color)
%coord为给出的点的坐标,为 n by 2 的向量,第一列为点的x坐标,第二列为点的y坐标
%我们画出以这些点为中心,边长为1的填充正方形 color为颜色 如color = 'k'时,表示黑色
for i = 1:length(coord(:,1))
x = coord(i,1);
y = coord(i,2);
X = [x-0.5,x+0.5,x+0.5,x-0.5];
Y = [y-0.5,y-0.5,y+0.5,y+0.5];
fill(X,Y,color);
hold on;
end
axis equal;
end