Randomized Online PCA Algorithms with Regret Bounds that are Logarithmic in the Dimension
文章目录
- Setup of Batch PCA and Online PCA
- Hedge Algorithm
- 改进算法
- 用于矩阵
- $rounding()$
前俩次,都用到了 r o u n d i n g ( ) rounding() rounding(),遗憾的是,都没有讲清楚,这次稍微具体地讲下这篇论文。但是说实话,我感觉,我还是没有领会到这篇文章的精髓。
Setup of Batch PCA and Online PCA
Batch PCA的目标,就是寻找一个子空间,能够最小化平方误差。
这篇论文,给出了一个比较新颖的表达方式:
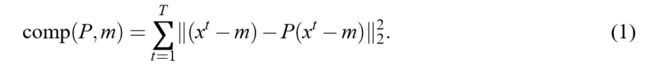
where,
m ∈ R n m\in \mathbb{R}^{n} m∈Rn
r a n k ( P ) = k rank(P) =k rank(P)=k
一般来讲,最优解就是, m = x ‾ m = \overline{x} m=x, 而 P P P所对应的子空间就是协方差矩阵的前 k k k个特征向量组成的子空间。
论文对(1)进行了一个改写:
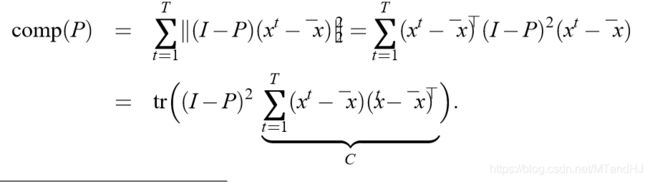
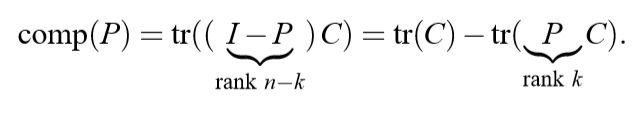
上面式子的一种直观解释就是, c o m p ( P ) comp(P) comp(P)就是一种损失,这个损失是由投影矩阵 P P P带来的。
而在streaming PCA(论文里为Online PCA):
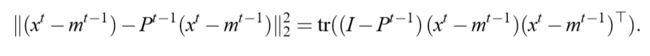
很自然的,
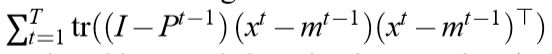
成了 T T T次迭代所积累的损失。
我们希望,这些损失,能够接近由Batch PCA所产生的损失。
Hedge Algorithm
假设,有 n n n个专家:expert i i i, i = 1 , 2 , … , n i=1,2,\ldots,n i=1,2,…,n.
有一个概率向量 w \mathsf{w} w,每个元素 w i \mathsf{w}_i wi为舍弃expert i i i的概率。
自然而然,会有一个损失,称之为: l \mathcal{l} l,每个元素是舍弃相应expert的损失,但是要求 l ∈ [ 0 , 1 ] \mathcal{l}\in[0,1] l∈[0,1],所以我估计得有个单位化的过程。
下面就是如何选取专家,和迭代更新 w \mathsf{w} w的算法。

这个 w \mathbf{w} w的更新,有点类似adaboost,感觉其它地方也有看到过,至于其中的原理,估计还是得看论文吧。
同时,有下面的性质:


改进算法
这个算法的目标是,将 w \mathbf{w} w分解为 ∑ i p i r i \mathop{\sum}\limits_{i}p_ir_i i∑piri,其中 p i p_i pi为概率, r i r_i ri为 ( n − k ) (n-k) (n−k)-corner. d d d-corner,是指有且仅有 d d d个非零项,且非零项的值为: 1 d \frac{1}{d} d1.分解完毕只有,不同于上面的算法,这个算法将通过分布 p i p_i pi选择 r i r_i ri,而 r i r_i ri中的非零项所对应的指标就是相应的要舍弃的专家,expert。
分解算法如下:

w ∈ B d n \mathbf{w} \in B_d^n w∈Bdn是指 ∣ w ∣ = ∑ i w i = 1 |\mathbf{w}|=\mathop{\sum}\limits_{i}\mathbf{w}_i=1 ∣w∣=i∑wi=1,且 0 ≤ w i ≤ 1 d 0 \leq \mathbf{w}_i \leq \frac{1}{d} 0≤wi≤d1
为了使 w ∈ B d n \mathbf{w} \in B_d^{n} w∈Bdn,有下面的算法:

用于矩阵
矩阵 d d d-corner是指 A A A的特征值,有且仅有 d d d个非零项,且均为 1 d \frac{1}{d} d1。
其他的类似定义。
这里的 W W W是密度矩阵:对称正定矩阵,且迹为1。
则:

![]()
l o g A = ∑ i l o g ( λ i ) a i a i ⊤ \mathbf{log}A=\mathop{\sum}\limits_ilog(\lambda_i)a_ia_i^{\top} logA=i∑log(λi)aiai⊤, 如果 A = ∑ i λ i a i a i ⊤ A=\mathop{\sum}\limits_i\lambda_ia_ia_i^{\top} A=i∑λiaiai⊤
e x p A \mathbf{exp}A expA同理。
这个算法貌似是为了将 W W W投影到 B d n B_d^{n} Bdn中的理论依据。
r o u n d i n g ( ) rounding() rounding()
那么如何将上面的种种算法应用到之前提到的文章呢。之前的文章说,算法二就可以了,所以是这么理解吗?
最后得到的矩阵,根据特征值,得到概率向量 w \mathbf{w} w,然后再进行分解,通过概率 p i p_i pi,得到 r i r_i ri,接着,舍弃这些特征向量,得到最后的投影矩阵 P P P?
但是,用特征值,总觉得和上面的不大相符,可不用特征值又能用什么呢?因为他们都是在最后一步利用这个 r o u n d i n g ( ) rounding() rounding()。但是,用算法五,就和他们本身的算法不一致了,具体如何,不得而知了。