分类和回归树，随机森林，霍夫森林（CART，random forests，hough forests）

1. 分类和回归树（CART，classification and regression tree）

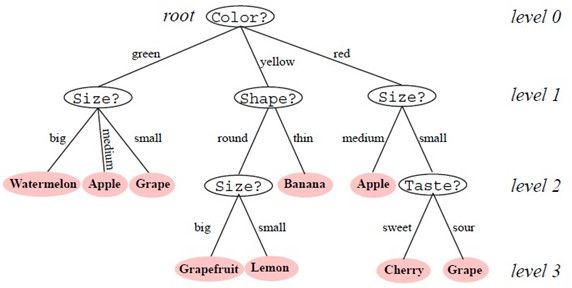
          基于树的方法的思路：把特征空间划分成一系列的矩形区域，然后在每个区域中拟合一个简单的模型（例如：常量）。下图是决策树（decision tree）的一个简单示意：

下面分别介绍回归树和分类树。

1.1 回归树（regression tree）

如何逐步生成回归树？给定（输入、响应）组成的N个观测，如何自动确定分裂变量、分裂点，以及树的结构。

第一步：搜索分裂变量和分裂点。假设将空间划分为M个区域，每个区域用对响应建模。在二叉划分中，假设搜索分裂变量j和分裂点s，定义一对半平面：

 

搜索分裂变量j和分裂点s的目标函数为：

内部极小化可以用下式求解：

第二步：树结构的控制。涉及两个方面，一个是何时停止分裂，另一个是对树进行剪枝。

何时停止分裂有两种方法：一种是仅当分裂是平方和的降低超过某个阈值时，才分裂；另一种是仅当达到最小节点大小时停止分裂。

对树进行剪枝：思路是定义树的一些子树，从它们中找到在“对数据拟合程度 + 树模型的复杂度”准则下最优的一个，如下式：

 其中：

参数来控制树的大小和对数据拟合程度之间的折中，对它的估计用5或10折交叉验证实现。

1.2 分类树（classification tree）

跟回归树相比，主要是分裂节点和修剪树的准则不同。首先定义节点m中类k的观测比例为：

 分裂准则常用下面三个“误分类不纯度”、“Gini不纯度”、“熵不纯度”：

分裂时，找到使不纯度下降最快的分裂变量和分裂点。不纯度的下降落差可以直观的定义为：

剪枝时，最常用的是“误分类不纯度”准则。

另外：三个准则在2类分类时节点不纯度的函数图为：

从图中可以看出“Gini不纯度”、“熵不纯度”可微，更适合数值优化。

1.3 优缺点

树的主要优点是：直观，有可以理解的规则；计算量相对来说不大等等。

主要缺点：

（1）有较高的方差，数据较小的变化会导致完全不同的分裂。Bagging通过对许多树求平均来降低方差。

（2）预测面缺乏光滑性，这点主要影响回归的效果，改进的方法为：MARS（多元自适应回归样条）。

2. 随机森林（random forests）

        随机森林是一个用随机方式建立的，包含多个决策树的分类器。其输出的类别是由各个树输出的类别的众数而定。

        随机性主要体现在两个方面：（1）训练每棵树时，从全部训练样本中选取一个子集进行训练（即bootstrap取样）。用剩余的数据进行评测，评估其误差；（2）在每个节点，随机选取所有特征的一个子集，用来计算最佳分割方式。

        随机森林的主要优点：（1）在大的、高维数据训练时，不容易出现过拟合而且速度较快；（2）测试时速度很快；（3）对训练数据中的噪声和错误鲁棒。

        OpenCV 中提供了Random forest 的函数：CvRTrees::train，CvRTrees::predict等。

3. 霍夫森林（hough forests）

         霍夫森林是随机森林和霍夫投票在计算机视觉中的应用，用在物体检测，跟踪和动作识别。主要特点是：

         （1） 每个叶子节点都是一个判别性的码本，对到达这个叶子节点的patch做出一个预测：它来自前景的概率是多少？它距离物体中心有多远？

         （2） 在节点分裂的时候，随机选择类别不纯度或是偏移量不纯度：

 

4.  Bagging vs. Random forests
      tong zhang老师课件中对二者的表述，言简意赅。

 

参考：

  《模式分类》 第二版

 The Elements of Statistical Learning

 Wiki :  Decision tree      Random forest

  决策树模型组合之随机森林与GBDT 

  Class-Specific Hough Forests for Object Detection 

 Random Forest and Its Applications , Liang Wang
 龙星计划： 机器学习