相机参数说明
1.为什么需要标定相机?
主要因为生产的相机成像传感器不是很完美,另外镜头与成像面不是水平的,而是有夹角的,所以通过相机看到的物体的位置与物体实际的位置像是不匹配的。
2.相机标定的内外参数说明
内参数主要为相机的基础矩阵M和畸变向量dist,分别表示为
M = [ f x 0 u 0 0 f y v 0 0 0 1 ] \begin{gathered} M= \begin{bmatrix} f_{x} & 0 & u_{0} \\ 0 & f_{y} & v_{0} \\0&0&1 \end{bmatrix} \quad \end{gathered} M=⎣⎡fx000fy0u0v01⎦⎤
d i s t = [ k 1 , k 2 , p 1 , p 2 , k 3 ] dist = [k_{1}, k_{2},p_{1},p_{2},k_{3}] dist=[k1,k2,p1,p2,k3]
其中 ( f x , f y ) (f_{x}, f_{y}) (fx,fy)是焦距, ( u 0 , v 0 ) (u_{0},v_{0}) (u0,v0)为焦点坐标
径向畸变 [ k 1 , k 2 , k 3 ] [k_{1}, k_{2},k_{3}] [k1,k2,k3]:这是由于透镜先天条件原因(透镜形状),成像仪中心(光学中心)的畸变为0,随着向边缘移动,畸变越厉害。这里有3个参数,k1,k2,k3其中k3是可选参数。
切向畸变 [ p 1 , p 2 ] [p_{1},p_{2}] [p1,p2]:这是摄像机安装过程造成的,如当透镜不完全平行于图像平面的时候产生的。
外参主要是旋转矩阵 R 3 ∗ 3 R_{3*3} R3∗3和平移向量 T = [ t 1 , t 2 , t 3 ] T=[t_{1}, t_{2}, t_{3}] T=[t1,t2,t3]。
[ x y 1 ] = [ f x 0 u 0 0 f y v 0 0 0 1 ] [ r 1 r 2 r 3 t 1 r 4 r 5 r 6 t 2 r 7 r 8 r 9 t 3 ] [ X Y Z 1 ] \begin{gathered} \begin{bmatrix} x \\ y \\1 \end{bmatrix}= \begin{bmatrix} f_{x} & 0 & u_{0} \\ 0 & f_{y} & v_{0} \\0&0&1 \end{bmatrix} \begin{bmatrix} r_{1} & r_{2}& r_{3} & t_{1}\\ r_{4} & r_{5} & r_{6} & t_{2}\\ r_{7}& r_{8}& r_{9}& t_{3} \end{bmatrix} \begin{bmatrix} X \\ Y \\Z\\1 \end{bmatrix} \quad \end{gathered} ⎣⎡xy1⎦⎤=⎣⎡fx000fy0u0v01⎦⎤⎣⎡r1r4r7r2r5r8r3r6r9t1t2t3⎦⎤⎣⎢⎢⎡XYZ1⎦⎥⎥⎤
(x,y)是图像平面的物理坐标,(X,Y,Z)为实际的世界坐标。它们的关系就是x=M*[R][T]*X,所以相机标定的内外参数是关乎物体实际坐标到相机图像的物理坐标的转换。
相机的外参和内参是不同的,内参是固定的不会变化,求出以后都可以直接使用,而外参是是决定世界坐标系到相机左标系的转换,如果相机位置改变,外参也会改变。所以决定单目相机的外参和双目相机的外参也有所不同,双目相机的外参是指一个相机相对于另一个相机的位置坐标变化,所以双目相机的两个摄像头固定后,其外参也是固定的,我们可以基于外参用来测距、求深度图等
3.坐标变换
我们在相机标定(视觉定位)要考虑的问题:
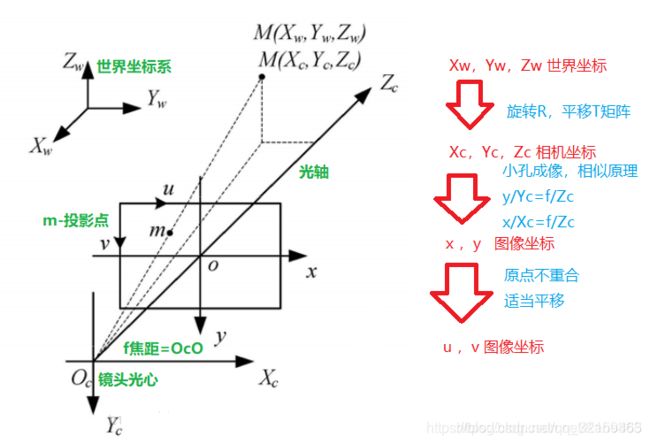
1.世界坐标←→相机坐标
就是将物体在世界中的坐标对应到相机坐标中,在这个过程中需要相机的外参:旋转矩阵R和平移向量T。
2.相机坐标←→图像的物理坐标
在这个过程中,是一个光学投影的过程,需要使用到相机的内参:焦距f、焦点坐标(u0,v0)等,也就是相机的基本矩阵。
3.图像的物理坐标←→图像的像素坐标
这个过程就是在步骤2的基础上,将物理坐标中的单位距离mm转换为像素pixel个数。
解决以上三个变换,我们就可以将世界坐标中的点和图像中的像素随意转换了。
另配图一幅加以理解:

具体标定过程请移步
1.单目相机标定python+opencv
2.双目相机标定matlab
参考:1.https://blog.csdn.net/weilixin88/article/details/91603319