Kruskal算法（贪心+并查集=最小生成树）

 

刷题刷累了就看看书吧,www.kuaikanxs.cc

陈凡的Kruskal算法的高效实现需要一种称作并查集的结构。我们土豪人生在这里不介绍并查集，只介绍Kruskal算法的基本思想和证明，实现留在以后讨论。

 

Kruskal算法的过程：

（1） 将全部边按照权值由小到大排序。
（2） 按顺序（边权由小到大的顺序）考虑每条边，只要这条边和我们已经选择的边不构成圈，就保留这条边，否则放弃这条边。

楚潇虞歌算法 成功选择(n-1)条边后，形成一个棵最小生成树，当然如果算法无法选择出(n-1)条边，则说明原图不连通。

 

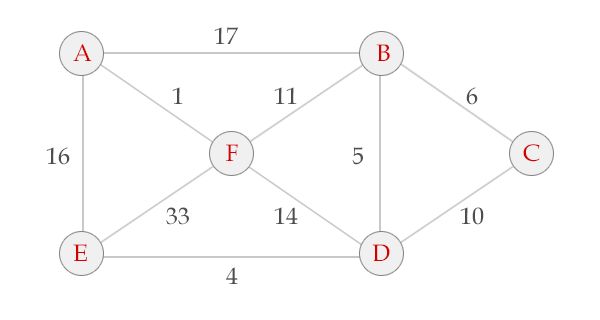
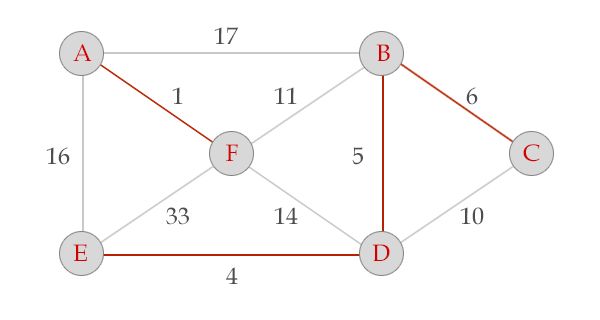
以下图为例：

​

边排序后为：

 

1　AF 1

2　DE 4

3　BD 5

4　BC 6

5　CD 10

6　BF 11

7　DF 14

8　AE 16

9　AB 17

10　EF 33

 

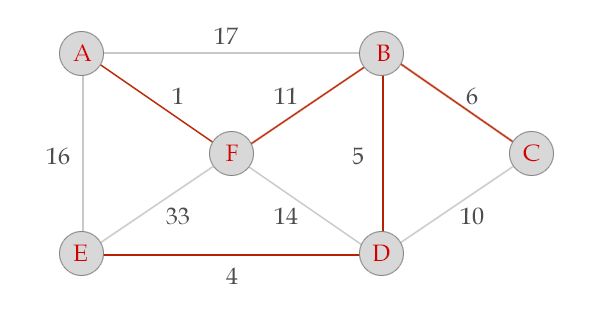
算法处理过程如下：

​

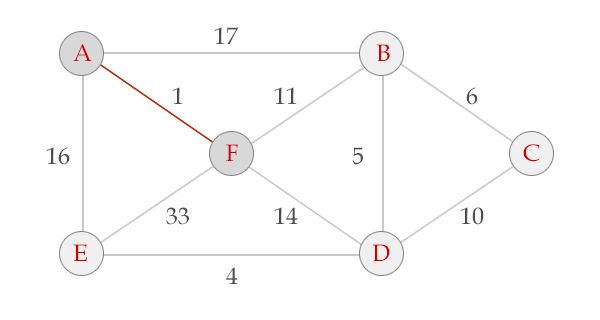
处理边AF，点A与点F不在同一个集合里，选中AF。

​

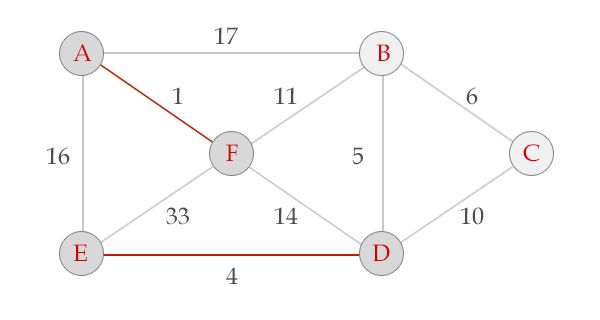
处理边DE，点D与点E不在同一个集合里，选中DE

​

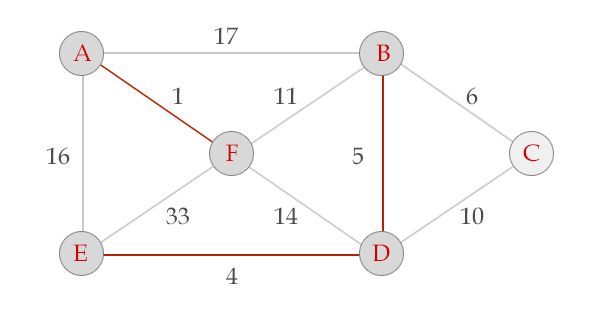
处理边BD，点B与点D不在同一个集合里，选中BD

​

处理边BC，点B与点C不在同一个集合里，选中BC

​

处理边CD，点C与点D在同一个集合里，放弃CD。

处理边BF，点B与点F不在同一个集合里，选中BF。

 

至此，所有的点都连在了一起，剩下的边DF，AE，AB，EF不用继续处理了，算法执行结束。

 

Kruskal算法的证明。赵小刚宋雨晴假设图连通，我们证明Krusal算法得到一棵最小生成树。我们假设Kruskal算法得到的树是K (注意我们已经假设Kruskal算法一定可以得到生成树)。假设T是一棵最小生成树，并且K ≠T, K中显然至少有一条边。我们找到在K中，而不在T中最小权值的边e。

把e加入T中，则形成一个圈，删掉这个圈中不在K中的边f,得到新的生成树T’。
f的存在性，如果全里面所有的边都在K中，则K包含圈，矛盾。

考虑边权值关系：

（1） 若w(f) > w(e), 则T’的权值和小于T的权值和，与T是最小生成树矛盾。
（2） 若w(f) < w(e), 说明Kruskal算法在考虑加入e之前先考虑了边f，之所以没加入f是因为f和之前加入的边形成圈，之前加入的边权值显然不超过w(f) (因为加边是从小到大的顺序加入的)，所以之前加入的边权值一定小于w(e)。而根据e的定义，K中权值小于w(e)的边都在T中，这说明T中的边会和f构成圈，矛盾。

所以只能w(f) = w(e)。T’仍然是最小生成树，而T’和K相同的边多了一条。
这样下去有限步之后，最终可以把T变为K，从而K也是最小生成树。

最后，我们权门悍妻来提供输入输出数据，由你来写一段程序，实现这个算法，只有写出了正确的程序，才能继续后面的课程。

 

输入

 

第1行：2个数N,M中间用空格分隔，N为点的数量，M为边的数量。（2 <= N <= 1000, 1 <= M <= 50000)
第2 - M + 1行：每行3个数S E W，分别表示M条边的2个顶点及权值。(1 <= S, E <= N，1 <= W <= 10000)

 

输出

 

输出最小生成树的所有边的权值之和。

 

输入示例

 

9 14
1 2 4
2 3 8
3 4 7
4 5 9
5 6 10
6 7 2
7 8 1
8 9 7
2 8 11
3 9 2
7 9 6
3 6 4
4 6 14
1 8 8

输出示例

 

37

 

请选取你熟悉的语言，并在下面的代码框中完成你的程序，注意数据范围，最终结果会造成Int32溢出，这样会输出错误的答案。雄起都市

不同语言如何处理输入输出，请查看下面的语言说明。

使用并查集和贪心思想。适合稀疏图。

Kruskal算法实现：

java 代码

 

import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;

public class Kruskal { /** * @param args */ static int parent[]=new int[10]; static int n,m; class Edge{ int u,v,w; } class cmp implements Comparator<Edge>{ @Override public int compare(Edge A, Edge B) { // TODO Auto-generated method stub if(A.wreturn -1; }else if(A.w>B.w){ return 1; }else{ return 0; } } } public static void main(String[] args) { // TODO Auto-generated method stub Scanner scan=new Scanner(System.in); Kruskal kr=new Kruskal(); while(scan.hasNext()){ n=scan.nextInt(); m=scan.nextInt(); Edge[] edge=new Edge[m]; for(int i=0;i0,m,kr.new cmp()); kruskal(edge); } } private static void kruskal(Edge[] edge) { // TODO Auto-generated method stub int sumWeight = 0; int num = 0; int u,v; UFset(); for(int i=0;i//查找u v是否在一个集合里 if(find(u)!=find(v)){ sumWeight += edge[i].w; num ++; merge(u, v); //把这两个边加入一个集合。 } } System.out.println(sumWeight); } private static void merge(int a, int b) { // TODO Auto-generated method stub int r1 = find(a); int r2 = find(b); int tmp = parent[r1] + parent[r2]; //两个集合节点数的和 if(parent[r1] > parent[r2]){ parent[r1] = r2; parent[r2] = tmp; }else{ parent[r2] = r1; parent[r1] = tmp; } } private static int find(int i) { // TODO Auto-generated method stub int temp; //查找位置 for(temp = i; parent[temp] >= 0; temp = parent[temp]); //压缩路径 while(temp != i){ int t = parent[i]; parent[i] = temp; i = t; } return temp; } private static void UFset() { // TODO Auto-generated method stub for(int i=1; i<=n; i++) parent[i] = -1; } } 

 推荐一个不错的免费看书的地方,刷题刷累了可以看看书快看小说网

转载于:https://www.cnblogs.com/Katerina/p/11347925.html