并查集(Disjoint Set)

　　在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。

本文地址：http://www.cnblogs.com/archimedes/p/disjoint-set.html，转载请注明源地址。

定义

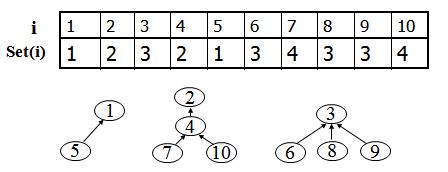
并查集（Disjoint Set），即“不相交集合”，是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。集就是让每个元素构成一个单元素的集合，也就是按一定顺序将属于同一组的元素所在的集合合并。

将编号分别为1…N的N个对象划分为不相交集合，在每个集合中，选择其中某个元素代表所在集合。

常见两种操作：

• 合并两个集合
• 查找某元素属于哪个集合

用编号最小的元素标记所在集合；定义一个数组 set[1..n] ，其中set[i] 表示元素i 所在的集合；

算法实现

查找 Θ(1)

find1(x)
{
    return set[x];
}

合并 Θ(N)

Merge1(a,b)
{   
    i = min(a,b);
    j = max(a,b);
    for (k = 1; k <= N; k++) {
        if (set[k] == j)
            set[k] = i;
    }
}    

对于“合并操作”，必须搜索全部元素！有没有可以改进的地方呢？

算法的优化

使用树结构

每个集合用一棵“有根树”表示，定义数组 set[1..n]

• set[i] = i , 则i表示本集合，并是集合对应树的根
• set[i] = j, j<>i, 则 j 是 i 的父节点. 

查找 最坏情况Θ(N)

find2(x)
{
   r = x;
   while (set[r] != r)
      r = set[r];
   return r;
}

合并 Θ(1)

merge2(a, b)
{
    if (a<b)
       set[b] = a;
    else
       set[a] = b;
}

性能有无本质的改进？如何避免最坏情况呢？

优化--避免最坏情况

方法：将深度小的树合并到深度大的树

实现：假设两棵树的深度分别为h1和h2, 则合并后的树的高度h是:

max(h1,h2), if h1<>h2.

h1+1, if h1=h2.

效果：任意顺序的合并操作以后，包含k个节点的树的最大高度不超过lgk

优化后算法及效率：

查找 Θ(N)

find2(x)    
{
   r = x;
   while (set[r] != r)
      r = set[r];
   return r;
}

合并 Θ(1)

merge3(a,b)
{ 
    if (height(a) == height(b)) {
       height(a) = height(a) + 1;
       set[b] = a; 
    } else if (height(a) < height(b)) {
       set[a] = b;
    } else {  
       set[b] = a; 
    }
}

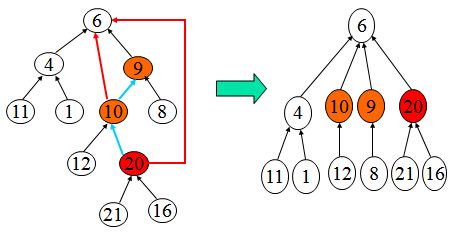
进一步优化--路径压缩

思想：每次查找的时候，如果路径较长，则修改信息，以便下次查找的时候速度更快

步骤:

• 第一步，找到根结点
• 第二步，修改查找路径上的所有节点，将它们都指向根结点

带路径压缩的查找算法：

find3(x)
{
      r = x;
      while (set[r]  !=  r) //循环结束，则找到根节点
          r = set[r];       
      i = x;
      while (i != r) //本循环修改查找路径中所有节点
      {   
          j = set[i];
         set[i] = r;
          i = j;
      }
}

路径压缩示意图:

编程实践

（HDOJ1232）畅通工程

某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？

典型的并查集题目

#include
int bin[1002];
int findx(int x)
{
    int r = x;
    while(bin[r] != r)
        r = bin[r];
    return r;
}
void merge(int x, int y)
{
    int fx, fy;
    fx = findx(x);
    fy = findx(y);
    if(fx != fy)
        bin[fx] = fy;
}
void solve()
{
    int n, m, i, x, y, count; 
    while(scanf("%d", &n), n) {
        for(i = 1; i <= n; i++)
            bin[i] = i;
        for(scanf("%d", &m); m > 0; m--) {
            scanf("%d %d", &x, &y);
            merge(x, y);
        }
        for(count = -1, i = 1; i <= n; i++) {
            if(bin[i] == i)
                count++;
        }
        printf("%d\n", count);
    }
}
int main()
{
    solve();
    return 0;
}

View Code

 （HDOJ1272）小希的迷宫

算法：

判断图是否连通且无回路

如果待连接的两点如果祖先节点相同，那么就构成回路，不符合

如果不构成回路，但是有多个根节点，也不符合

#include
#define N 100001
int set[N] = {0};
int findx(int x)
{
    int r = x;
    while(set[r] != r)
        r = set[r];
    return r;
}
void merge(int x, int y)
{
    int fx, fy;
    fx = findx(x);
    fy = findx(y);
    set[fy] = fx;
}
void solve()
{
    int flag, sum, i, x, y; 
    while(1) {
        flag = 0;
        while(scanf("%d %d", &x, &y) && (x || y)) {
            if(x == -1 && y == -1) return;
            if(set[x] == 0) set[x] = x;
            if(set[y] == 0) set[y] = y;
            if(findx(x) == findx(y)) {
                flag = 1;
            } else if(flag != 1) {
                merge(x, y);
            }
        }
        for(sum = 0, i = 1; i < N; i++) {
            if(set[i] == i) 
                sum++;
            set[i] = 0;
        }
        if(sum > 1 || flag == 1)
            printf("No\n");
        else
            printf("Yes\n");
    }
}
int main()
{
    solve();
    return 0;
}

View Code

 （HDOJ1558）Segment set

题目大意：

给你一些操作，P后边输入四个值，分别代表一条线段的起点、终点坐标，

当输入Q时，后边输入一个整形值K，输出第k条线段所在的集合中包含的线段的个数

思路：并查集+计算几何线段相交

当输入P时，判断后边输入的线段的起点和终点时，判断跟之前的线段有没有相交，如果有相交，就merge（）合并，

如果输入的是Q时，就打印出当前线段所在集合的个数

#include
#include
#define N 1010
int set[N], num[N];
typedef struct P
{
    double x, y;
}point;

typedef struct E
{
    point a, b;
}edge;
edge e[N];

double min(double a, double b)
{
    return a > b ? b : a;
}

double max(double a, double b)
{
    return a > b ? a : b;
}

int find(int x) /*带路径压缩的查找算法*/
{
    int r, i, j;
    i = r = x;
    while(set[r] != r)
        r = set[r];
    while(i != r) {
        j = set[i];
        set[i] = r;
        i = j;
    }
    return r;
}

void merge(int x, int y)
{
    int fx, fy;
    fx = find(x);
    fy = find(y);
    if(fx != fy) {
        set[fx] = fy;
        num[fy] += num[fx];
    }
}

/********计算几何（判断线段相交函数）**************/
double xmult(point a, point b, point c) /*大于零代表a,b,c左转*/
{  
    return (b.x - a.x)*(c.y - a.y) - (b.y - a.y) * (c.x - a.x);  
}  
bool OnSegment(point a,point b,point c)         /* a,b,c共线时有效 */  
{   
    return c.x >= min(a.x,b.x) && c.x <= max(a.x,b.x) && c.y >= min(a.y,b.y) && c.y <= max(a.y,b.y);  
}  
bool Cross(point a,point b,point c,point d) /* 判断ab 与cd是否相交 */ 
{  
    double d1, d2, d3, d4;  
    d1 = xmult(c,d,a);  
    d2 = xmult(c,d,b);  
    d3 = xmult(a,b,c);  
    d4 = xmult(a,b,d);  
    if(d1 * d2 < 0 && d3 * d4 < 0)  return true;  
    else if(d1 == 0 && OnSegment(c, d, a)) return true;  
    else if(d2 == 0 && OnSegment(c, d, b)) return true;  
    else if(d3 == 0 && OnSegment(a, b, c)) return true;  
    else if(d4 == 0 && OnSegment(a, b, d)) return true;  
    return false;  
}  
/**********************/

void solve()
{
    int t, k, n, i, j, temp;
    char s[5];
    scanf("%d", &t);
    while(t--) {
        scanf("%d", &n);
        k = 0;
        for(i = 1; i <= n; i++) {
            set[i] = i;
            num[i] = 1;
        }
        for(i = 1; i <= n; i++) {
            scanf("%s", s);
            if(s[0] == 'P') {
                k++;
                scanf("%lf %lf %lf %lf", &e[k].a.x, &e[k].a.y, &e[k].b.x, &e[k].b.y);
                for(j = 1; j < k; j++) {
                    if(find(k) != find(j) && Cross(e[k].a, e[k].b, e[j].a, e[j].b))
                        merge(k, j);
                }
            } else if(s[0] == 'Q') {
                scanf("%d", &temp);
                printf("%d\n", num[find(temp)]);
            }
        }
        if(t) printf("\n");
    }
}

int main()
{
    solve();
    return 0;
}

View Code

 

参考资料：

杭电--A​C​M​算​法​之​并​查​集