Heap——堆、二叉堆——堆排序——优先队列

---

堆(Heap)

  堆源自于1964年威廉姆斯发表的堆排序，当时他提出用二叉堆树来作为此算法的数据结构，所以我们一般讲堆这个数据结构，指的就是二叉堆。

---

二叉堆

  二叉堆是完全二叉树或近似于完全二叉树，一般使用数组来存储。

• 如果根节点在数组中的位置是1，则第i个位置的左儿子的位置为2i，右儿子的位置为2i+1
• 如果根结点在数组中的位置是0，则第i个位置的左儿子的位置为2i+1,右儿子的位置在2i+2

最大堆

  满足二叉堆情况下，父结点的键值总是大于或等于子节点的键值,最大堆中的最大元素在根结点

    即  $A[PARENT(i)]\ge A[i]$

  举例: 设根节点在数组的位置是1，下列这个最大堆在数组中的存储如下图所示

最小堆

  满足二叉堆情况下，父结点的键值总是小于或等于子节点的键值，最小堆的最小元素在根节点

    即  $A[PARENT(i)]\le A[i]$

---

堆的基本操作

对堆的基本操作最重要的是维护堆的性质(Max-Heapify)，需要让这个堆满足最大堆的性质或最小堆的性质。其次是建堆(Build-Max-Heapify)，给定一个无序的树，将其建立成一个最大堆或最小堆，下面将详细介绍这两个操作

---

维护堆的性质(Max-Heapify)

  以最大堆为例，输入为一个数组$A$和一个下标i,在调用Max-Heapify的时候，我们假设$Left(i)$和$Right(i)$都是最大堆，这时有可能$A[i]$小于其左右孩子，这是我们就需要找到左右孩子中的最大孩子max，将这个最大孩子$max$和$A[i]$交换，交换完后可能孩子结点的最大堆性质也被破坏了，这个时候就需要递归维护堆的性质。下面举例说明:



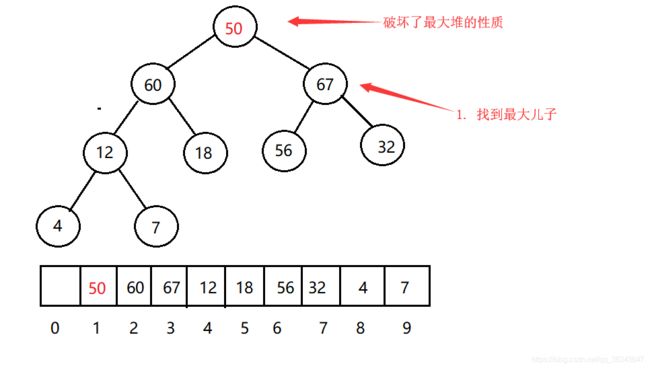
从图中我们可以推导出，步骤3和步骤4是重复的，可以形成递归。当然我们也可以不使用递归而直接使用循环来实现，下面给出递归版和非递归版

	/**
	 * 递归版本Max-Heapify
	 * 大前提: 
	 * 		这个二叉堆的儿子都已经是最大堆!!!
	 * 使用递归方法调整成最大堆
	 * @param arr	需要调整的二叉堆
	 * @param position	调整的位置
	 * @param size	二叉堆的大小
	 */
	private void adjustToMaxHeapify(int[] arr,int position,int size) {
		// 1. 寻找最大值
		int maxIndex = position;	// 默认最大值的索引
		int leftIndex = position * 2 + 2;	// 左儿子的索引
		int rightIndex = position *2 + 1;	// 右儿子的索引
		if(leftIndex < size) 
			if(arr[maxIndex] < arr[leftIndex]) maxIndex = leftIndex;
		if(rightIndex < size)
			if(arr[maxIndex] < arr[rightIndex]) maxIndex = rightIndex;
		/*
		 * 2. 互换数据并递归
		 * 如果maxIndex不和position相等，说明position处的值比儿子小
		 * 需要调整maxIndex和position的值
		 * 递归调整maxIndex处的值，因为maxIndex处的性质可能已经被破坏
		 */
		if(maxIndex != position) {	// 递归终止条件
			arr[maxIndex] = arr[maxIndex] ^ arr[position];
			arr[position] = arr[maxIndex] ^ arr[position];
			arr[maxIndex] = arr[maxIndex] ^ arr[position];
			adjustToMaxHeapify(arr, maxIndex, size);
		}
	}
	/**
	 * 非递归版本Max-Heapify
	 * 大前提: 
	 * 		这个二叉堆的儿子都已经是最大堆!!!
	 * 
	 * 使用非递归方法将数组调整成最大堆
	 * @param arr	需要调整的最大堆
	 * @param position 需要调整的位置
	 * @param size 二叉堆的大小
	 */
	private void adjustToMaxHeapify2(int[] arr,int position,int size) {
		int temp = arr[position];
		// 默认maxIndex为position的左子结点
		for(int maxIndex = position*2+1; maxIndex < size ; maxIndex = maxIndex*2 +1) {	
			if(maxIndex+1 < size)	// 在堆的范围内操作
				if(arr[maxIndex] < arr[maxIndex+1])	// 说明左子结点的值小于右子结点的值
					maxIndex = maxIndex + 1;	// 将最大值索引指向右子结点
			if(arr[maxIndex] > temp) {	// 说明子节点大于初始的父节点,即第一个position位置的值
				arr[position] = arr[maxIndex];
				position = maxIndex; 	// 为下一次循环做准备，将position指向下一个点
			}else {
				break;	// 说明已经是最大堆了，不需要调整
			}
		}
		// 循环结束，已经将position为父节点的树的最大值放在了最顶
		arr[position] = temp;	// 将temp值放到了调整后的位置
	}

---

建堆(Build-Max-Heapify)

  建堆之前我们需要先对二叉堆进行进一步分析

  结论:
    当用数组表示存储$n$个元素的堆时
     叶结点下标分别是$(n/2)+1,(n/2)+2,...,n$
     非叶子结点下标分别是$(n/2),(n/2)-1,...,1$

  证明:
   设最后一个非叶子结点的位置为$i$,有左儿子，则其左儿子的下标为$2i+1$, 又设这个堆有$n$个元素，则有$n=2i+1$,即 $i=n/2(取整)$，故最后一个非叶子结点的位置为$n/2$,所以第一个叶子结点为$n/2+1$

  举例说明

利用上面得到的结论，我们就可以开始建堆了，从第一个非叶子结点开始维护堆的性质,直到根节点。从第一个非叶子结点开始建的原因是我们需要保证后面每一个需要维护的结点的孩子都是最大堆。下面给出实现:

	/**
	 * 构建最大堆，从第一个非叶子结点开始调整,即从基础的堆开始调整
	 * @param arr 
	 */
	public void buildMaxHeap(int[] arr) {
		int size = arr.length;
		for(int i = size/2; i >= 0 ; i--) {	// 从第一个非叶子结点开始调整			
			adjustToMaxHeapify(arr, i, size);
		}
	
	}

---

堆排序

  利用堆的性质，我们可以使用堆来进行排序，这种排序也被称为堆排序。以最大堆为例，根结点的值为堆中最大的值，我们将根结点和最后一个值交换，然后将最后一个位置从堆中剔除，然后再维护堆的性质，循环上面的操作直到最后一个值，此时我们得到的就是一个升序的数组。类似于最大堆，使用最小堆得到的是一个降序的数组。
下面是堆排序升序的实现

	/**
	 * 二叉堆排序
	 * @param arr 需要排序的数组
	 */
	public void maxHeapSort(int[] arr) {
		buildMaxHeap(arr);	// 先构建一个二叉堆
		for(int i = arr.length - 1 ; i > 0 ; i--) {
			arr[0] = arr[0] ^ arr[i];
			arr[i] = arr[0] ^ arr[i];
			arr[0] = arr[0] ^ arr[i];
			adjustToMaxHeapify2(arr, 0, i);
		}
	}

---

优先队列

  利用堆的性质，我们可以得到优先队列。使用最大堆得到的是最大优先队列，使用最小堆得到的是最小优先队列。优先队列常用于程序的优先调度中，如使用最大优先队列则优先权高的进程先执行。优先队列常用的操作有insert(T x)、findXxx()、deleteXxx()。下面给出一个最小优先队列的实现

import java.util.Comparator;

public class BinaryHeap> {

	private static final int DEFAULT_CAPACITY = 10;
	private int currentSize;
	private T[] array;

	public BinaryHeap() {
		this(DEFAULT_CAPACITY);
	}

	public BinaryHeap(int capacity) {
		array = (T[]) new Comparable[capacity]; // 注意如何创建泛型数组
	}

	public BinaryHeap(T[] items) {
		currentSize = items.length;
		array = (T[]) new Comparable[items.length * 11 / 10];
		int i = 1;
		for (T t : items) {
			array[i++] = t;
		}
		buildHeap();
	}

	/*
	 * 上虑 将指定元素插入到合适的位置
	 */
	public void insert(T x) {
		if (currentSize == array.length - 1) // 扩容
			enlargeArray(array.length * 2 + 1);
		int hole = ++currentSize; // 获取到堆的大小
		// 对堆进行调整
		for (array[0] = x; x.compareTo(array[hole / 2]) < 0; hole /= 2)
			array[hole] = array[hole / 2];
		array[hole] = x;
	}

	public T deleteMin() throws UnderflowException {
		if (isEmpty())
			throw new UnderflowException("堆空");
		T minItem = findMin();
		array[1] = array[currentSize--];
		percolateDown(1);
		return minItem;
	}

	public T findMin() throws UnderflowException {
		if(isEmpty()) throw new UnderflowException("堆空");
		return array[1];
	}

	public boolean isEmpty() {
		return currentSize == 0;
	}

	public void makeEmpty() {
		for(int i = 0 ; i < array.length; i++) {
			array[i] = null;
		}
	}

	// 调整
	private void percolateDown(int hole) {
		int child;
		T tmp = array[hole];
		for (; hole * 2 <= currentSize; hole = child) {
			child = hole * 2;
			if (child != currentSize)
				if (array[child + 1].compareTo(array[child]) < 0)
					child++;
			if (array[child].compareTo(tmp) < 0)
				array[hole] = array[child];
			else
				break;
		}
		array[hole] = tmp;
	}

	private void percolateDown2(int position) {
		T tmp = array[position];
		for (int min = position * 2; min < currentSize; min = min * 2) {
			if (min + 1 < currentSize)
				if (array[min].compareTo(array[min + 1]) < 0)
					min = min + 1;
			if (array[min].compareTo(tmp) < 0) {
				array[position] = array[min];
				position = min;
			} else
				break;
		}
		array[position] = tmp;
	}

	private void buildHeap() {
		for (int i = currentSize / 2; i > 0; i--) {
			percolateDown(i);
		}
	}

	private void enlargeArray(int newSize) {
		if(newSize < array.length) return;
		T[] newArr = (T[]) new Comparator[newSize];
		for(int i = 0 ; i < array.length ; i++) {
			newArr[i] = array[i];
		}
		array = newArr;
	}

}

---

当然，上述只是堆的基础知识，关于堆还有很多扩展的数据结构，如左式堆、$d$-堆、斜堆、二项式堆、斐波那契堆(后面介绍)等