算法基础知识学习——非线性比较排序算法
算法学习系列
1、冒泡排序。
主要思想:每轮遍历,都进行两两交换,将大数往后排列。直接上python代码,简单易懂:
def bubbleSort(sortList):
#冒泡排序
for i in range(len(sortList)):#进行len(sortList)轮的比较
for j in range(len(sortList)-i-1):#每一轮在比较的时候下标取到长度减去1防止下标越界
if sortList[j]<sortList[j+1]:
sortList[j+1],sortList[j]=sortList[j],sortList[j+1]
return sortList
2、选择排序
主要思想:选择排序实际上比较的次数跟冒泡是一样的,只是降低交换的次数,冒泡排序是通过两两的交换将最大值或者最小值浮出水面,而选择排序则是首先遍历出最大值或最小值,每次与该轮的最后一个值进行交换,这样就降低了交换的次数。
def selectSort(sortList):
for i in range(len(sortList)-1,-1,-1):
maxIndex=i
for j in range(i+1):#下标是i但是需要从i+1个数字里面找出最大的
if sortList[j]>sortList[maxIndex]:
maxIndex=j
sortList[maxIndex],sortList[i]=sortList[i],sortList[maxIndex]
return sortList
3、插入排序
主要思想:就像打扑克牌一样,每次选取的元素插入已有的序列里都按顺序进行插入,一直保持已有的序列有序。一般人在做的时候都是先开辟一块新的内存用作存放有序的这个数列。如下:
def insertSort(sortList):
result = []
for cirle,value in enumerate(sortList):
if len(result)==0 :
result.append(value)
else:
for index in range(len(result)+1):##其实对比了len(result)+1次
if (index==0 and value<=result[index]):
result.insert(index,value)
break
elif(index==(len(result)) and value>=result[index-1]):##边界条件
result.append(value)
break
elif(result[index-1]<=value and result[index]>=value ):
result.insert(index,value)
break
print("第%s次的结果"%cirle,result)
return result
下面讲不用开辟新的内存的方法。首先将遍历到的这个数据元素提取出来,这样相应的位置就空了,然后像推箱子一样从前往后推,推到提出来的这个元素应该放的位置,再放进去:
def insertSortDeng(sortList):
for index in range(1,len(sortList)):
thisValue=sortList[index]#提起来这个数
position=index-1 #从当前位置的前一个位置开始
while position>=0 and sortList[position]>thisValue:#让后移过程停下来的两个条件1、指针指向边界了2有位置比这个数小了,只要小了,就把这个位置填上数
sortList[position+1]=sortList[position]
position-=1
sortList[position+1]=thisValue##帮value放在这个位置上
return sortList
sortList=[1,1,3,5,8,3,2,9,4]
4、谢尔排序
主要思想:连续的调用若干次的插入排序,每一次都在小的规模上进行插入排序,然后缩短间隔,整个数列渐渐的趋于有序,所以在最后一次排序的时候就能尽可能少的进行交换和比较。
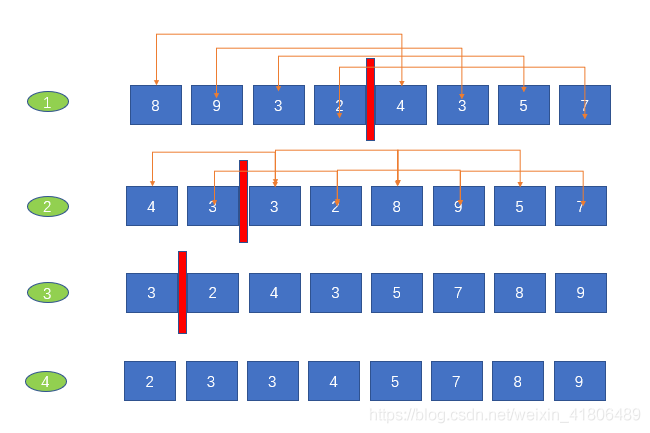
首先对该列数以4(1->2)为间隔进行插入排序,随后以2为间隔进行插入排序(2->3),最后以1为间隔进行插入排序(3->4),算法结束。
def shellOrder(lenGap,sortList):
for i in range(lenGap):
###接下来要进行lenGap次的排序
for j in range(i+lenGap,len(sortList),lenGap):##第一项不动,初始位置从i的后面取
thisValue=sortList[j]#将这个数提起来
beginPosition = j-lenGap#开始比较的位置是当前提起来数值的上一个
while beginPosition>=0 and thisValue<sortList[beginPosition]:
sortList[beginPosition+lenGap]=sortList[beginPosition]##往后拉一位
beginPosition-=lenGap
sortList[beginPosition+lenGap]=thisValue##一旦不满足条件,将当前值插入到当前指针的后一个位置
return sortList
sortList=[9,1,3,5,8,3,2,9,4]
lenGap=len(sortList)//2
while lenGap>=1:
sortList=shellOrder(lenGap,sortList)
lenGap=lenGap//2
5、归并排序
主要思想:首先将数据二等分,随后将二等分后的数据继续二等分,直至左边数据或右边数据为空或者为1,最后递归的将数据有序的合并起来。直接上代码,更能说明情况:
def merginSort(sortList):##用递归实现归并排序
if len(sortList)<=1:
return sortList
##否则反复调用该程序对左右进行排序
midIndex=len(sortList)//2
left=merginSort(sortList[:midIndex])
right=merginSort(sortList[midIndex:])
mergeResult=[]
while left and right:
if left[0]<right[0]:
mergeResult.append(left.pop(0))
else:
mergeResult.append(right.pop(0))
mergeResult.extend(right if right else left)
return mergeResult
sortList=[1,1,3,5,8,3,2,9,4]
print(merginSort(sortList))
6、快速排序
主要思想:每次从数列中选择出一个数字(这里涉及到选择得策略,是随机还是其他,本代码示例中每次从数列得最后选择一个数据)。然后以该数字为分界线左边都是小于该数得数,该数字得右边都是大于该数得数字。然后递归的执行该过程直到整个数列有序。
补充说明:下面代码中inplaceQuickSort不是真正得原地快速排序,因为虽然它没有开辟新得内存数组,但是在递归得过程中,python开辟了新得递归栈桢,所以它不是真正意义上得不开辟新内存下得排序方法。但是tureInplaceQickSort,通过循环实现尾递归,在不开辟新得栈桢得情况下实现快速排序。
class quickSort:
def __init__(self,s):
self.s=s
def getMidNumber(self,s,a,b):
l = a
r = b-1
p = s[b]#以最后一个作为随机数
while l<=r:
while l<=r and s[l]<=p:
l+=1
while r>=l and s[r]>=p:
r-=1
if l<r:##交换位置
s[l],s[r]=s[r],s[l]
s[l],s[b]=s[b],s[l]
return l
def inplaceQuickSort(self,s,a,b):
#得到一个左边的将数组划为左边比s[l]小,右边比s[l]大的两部分
if a>=b:
return
m=self.getMidNumber(s,a,b)
self.inplaceQuickSort(s,a,m-1)
self.inplaceQuickSort(s,m+1,b)
def tureInplaceQickSort(self,s,a,b):
#若函数在尾位置调用自身(或是一个尾调用本身的其他函数等等),则称这种情况为尾递归。
#这种排序方法减少了开辟递归栈
while a<b:
l=self.getMidNumber(s,a,b)
if l-a<b-l:
self.tureInplaceQickSort(s,a,l-1)
a=l+1
else:
self.tureInplaceQickSort(s,l+1,b)
b=l-1
def solveByInplaceQuickSort(self):
self.inplaceQuickSort(self.s,0,len(self.s)-1)
return self.s
def solveByTureInplaceQickSort(self):
self.tureInplaceQickSort(self.s,0,len(self.s)-1)
return self.s
sortList=[9,1,3,5,8,3,2,9,4]
print(quickSort(sortList).solveByInplaceQuickSort())
sortList1=[9,1,3,5,8,3,2,9,4]
print(quickSort(sortList1).solveByTureInplaceQickSort())
7、堆排序
主要思想:通过构建一个完全二叉树,然后循环的从该二叉树的根节点删除该二叉树的最小元素,最终实现排序。
对于数列[5,6,9,7,4,8,2,10]过程如下图:
构建二叉堆

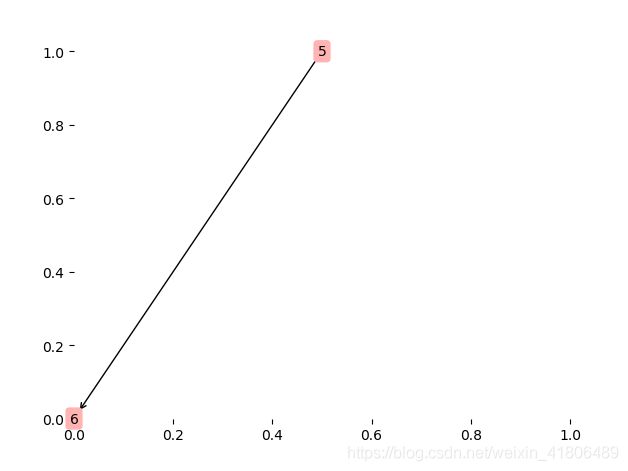

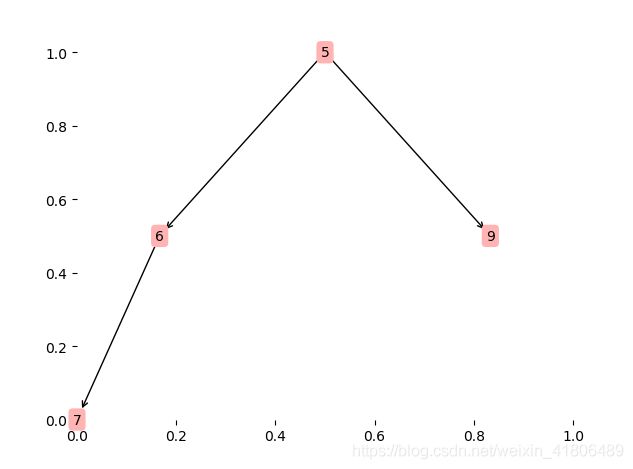
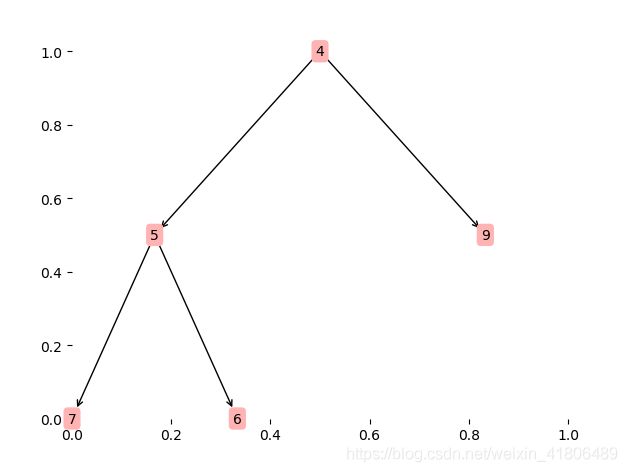
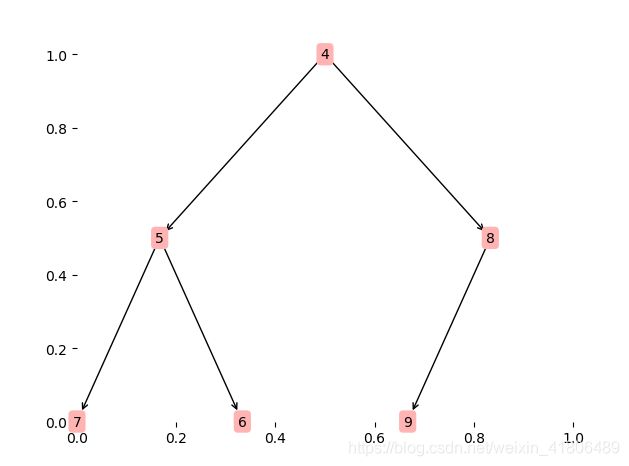

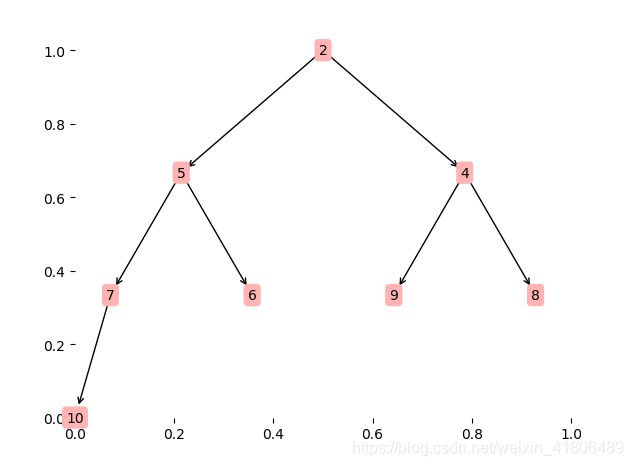
从栈顶删除二叉树
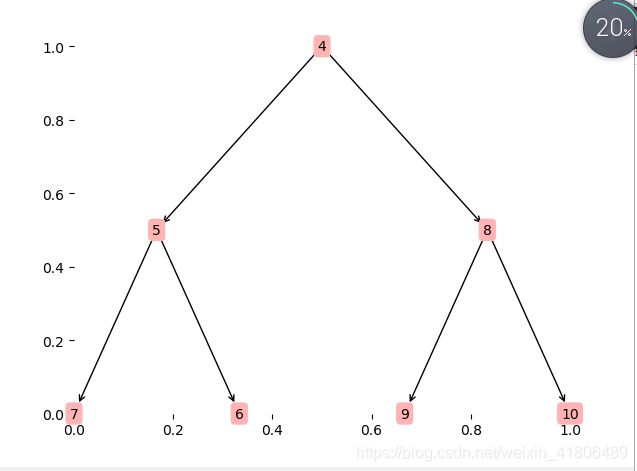
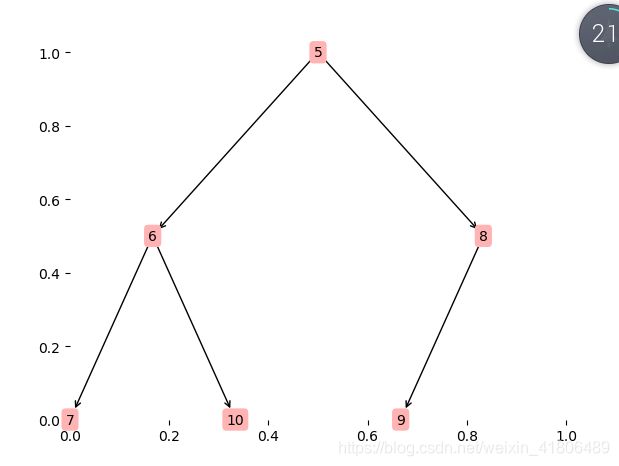
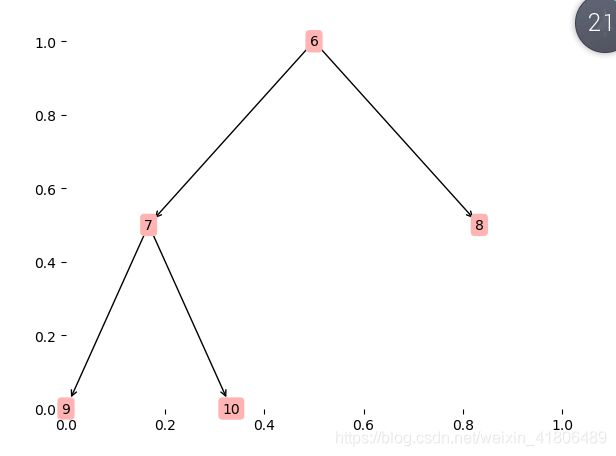
重复上述过程直到将所有的顶点删除,最终得结果。
class BinHeap:
def __init__(self):
self.heap=[0]#把首相填充,让列表从1位置开始填入数字
self.size=0
def perUp(self):
i=self.size
while i>1:
parI=i//2
if self.heap[parI]>self.heap[i]:
self.heap[parI],self.heap[i]=self.heap[i],self.heap[parI]
i=parI
def judgeLoR(self,i):##判断左孩子和右孩子哪一个比较小
leftIndex=2*i
rightIndex=2*i+1
if rightIndex>self.size:#说明没有右子树
return leftIndex
else:
if self.heap[leftIndex]<self.heap[rightIndex]:
return leftIndex
else:
return rightIndex
def perDown(self):
i=1#开始下沉的位置
while 2*i<self.size:#如果有左节点就进行下述操作
#判断跟左子树交换还是右子树交换
beChanged=self.judgeLoR(i)
if self.heap[beChanged]<self.heap[i]:
self.heap[i],self.heap[beChanged]=self.heap[beChanged],self.heap[i]
i=beChanged
def insert(self,value):#插入一个数据,在插入的时候需要上浮操作上浮到一个可以的位置
self.heap.append(value)
self.size+=1
#进行上浮操作
self.perUp()
def delMin(self):
##首先第一个位置和最后一个位置进行交换
if self.size==0:
return None
else:
self.heap[1],self.heap[-1]=self.heap[-1],self.heap[1]
beDeled=self.heap.pop()
self.size-=1
##首元素进行下沉操作
self.perDown()
return beDeled
def getHeap(self):
return self.heap
bh=BinHeap()
testList=[5,6,9,7,4,8,2,10]
for item in testList:
bh.insert(item)
while bh.size != 0:
print(bh.delMin())