【算法】分治法

二分搜索（二分查找、折半查找）

【要求】线性表为有序表（排好序的）
【基本思想】先确定待查找记录所在的范围，然后逐步缩小范围直至找到或找不到该记录位置。
【步骤】
1、先确定中间位置：middle = (left+right)/2;
2、将待查找得key值与data[middle].key值相比较。若相等，则查找成功并返回该位置，否则须确定新得查找区间，继续二分查找.如果data[middle].key大于key，right=middle-1。反之，data[middle].key小于key,left=middle+1。

//二分搜索算法
public class test{
    public static void main(String[] args){
        int[] a = {1,2,3,4,5,6,7,8,9};
        int position = bSearch(a,0,a.length-1,3);
        System.out.println(position);
    }
    public static int bSearch(int[] data,int left,int right,int key){
        //获取中间位置
        int middle = (left+right)/2;
        //三种情况
        if(data[middle] == key){
            return middle;
        }else if(data[middle] > key){
            return bSearch(data,left,middle-1,key);
        }else{
            return bSearch(data,middle+1,right,key);
        }
    }
}

汉诺塔

在汉诺塔游戏中，有三个分别命名为A、B、C得塔座，几个大小各不相同，从小到大一次编号得圆盘，每个原盘中间有一个小孔。最初，所有得圆盘都在A塔座上，其中最大得圆盘在最下面，然后是第二大，以此类推.

游戏的目的是将所有的圆盘从塔座A移动到塔座B;塔座C用来防止临时圆盘,游戏的规则如下:

1、一次只能移动一个圆盘

2、任何时候都不能将一个较大的圆盘压在较小的圆盘上面.

3、除了第二条限制,任何塔座的最上面的圆盘都可以移动到其他塔座上.

【解决思想】

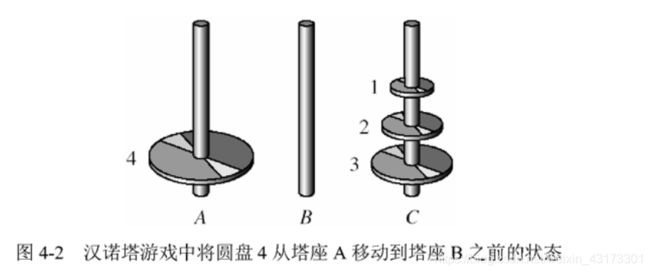
在解决汉诺塔问题时,事实上,我们不是关心圆盘1开始应该挪到哪个塔座上,而是关心最下面的圆盘4.当然,我们不能直接移动圆盘4,但是圆盘4最终将从塔座A移动到塔座B.按照游戏规则,在移动圆盘4之前的情况一定如下图

我们仍将分析,如何将前三个圆盘从A移动到C,然后圆盘4从A移动到B,前三个圆盘从C再移动到B.

但是上面的步骤可以重复利用!例如将三个圆盘从A移动到C,那么应该先将前两个圆盘从A移动到B,然后将圆盘3从A移动到C,最后将前两个圆盘从B移动到C.

持续简化这个问题,最终我们将只需要处理一个圆盘从一个塔座移动到另一个塔座的问题.

//汉诺塔
public class test{
    public static int count = 1;
    public static void main(String[] args){
        moved(4,"第一根柱子","第二根柱子","第三根柱子");

    }
    //i:圆盘数量
    //a:初始位置
    //b:最终位置
    //c:辅助位置
    public static void moved(int i,String a,String b,String c){
        if(i == 1){
            disPlay(1,a,b);
        }else{
            moved(i-1,a,c,b);
            disPlay(i,a,b);
            moved(i-1,c,b,a);
        }
    }
    public static void disPlay(int i,String a,String b){
        System.out.println("第"+count+"步：移动第"+i+"个塔从"+a+"到"+b);
        count++;
    }
}

合并排序（归并排序）

【归并排序思路】
将长度为n的待排序数组看做是由n个有序长度为1的数组组成
将其两两合并，得到长度为2的有序数组
然后再对这些子表进行合并，得到长度为4的有序数组
重复上述过程，一直到最后的子表长度为n也就完成了排序

一、合并两个有序数组

//合并排序（合并两个有序数组）
public class test{
    public static void main(String[] args){
        int[] a = {1,3,4,5,9};
        int[] b = {2,6,7,8,10};
        int[] result = merge2Arr(a,b);
        for(int i=0;i<result.length;i++){
            System.out.println(result[i]);
        }

   }
    public static int[] merge2Arr(int[] arr1,int[] arr2){
        int len1 = arr1.length;
        int len2 = arr2.length;
        int[]  result = new int[len1+len2];//新数组
        int i=0,j=0,k=0;
        while(i < len1 && j < len2){
            result[k++] = arr1[i] < arr2[j] ? arr1[i++] : arr2[j++];
        }
        while(i < len1){
            result[k++] = arr1[i++];
        }
        while(j < len2){
            result[k++] = arr2[j++];
        }
        return result;
    }

}

二、合并排序的递归实现

//合并排序（递归算法）
public class test {

    static int[] a = new int[] { 20, 9, 3, 5, 26, 100, 8, -1, 7, 50, -5 };

    public static void main(String[] args) {
        System.out.println("before sort");
        //ArrayUtils.printArray(a);
        for(int i=0;i<a.length;i++){
            System.out.println(a[i]);
        }
        //进行合并排序mergeSort
        mergeSort(a);
        System.out.println("after sort");
        for(int i=0;i<a.length;i++){
            System.out.println(a[i]);
        }
        //ArrayUtils.printArray(a);

    }

    private static void mergeSort(int[] k) {
        mSort(k, 0, k.length - 1);
    }

    private static void mSort(int[] k, int left, int right) {
        int center;
        // 递归退出条件，及left》=right的时候
        if (left < right) {
            // 找出中间索引
            center = (left + right) / 2;
            // 对左边数组进行递归
            mSort(k, 0, center);
            // 对右边数组进行递归
            mSort(k, center + 1, right);
            // 合并
            merging(k, left, center, right);

        }
    }

    private static void merging(int[] k, int left, int center, int right) {
       // 存放数据的数组
        int tempArr[] = new int[k.length];
        // third记录中间数组的索引
        int mid = center + 1;
        int third = left;//中间数组从左侧开始
        int temp = left;//先记录下初始左侧位置
        while (left <= center && mid <= right) {
            // 从左右两个数组找出最小的数存入tempArr数组
            if (k[left] < k[mid]) {
                tempArr[third++] = k[left++];
            } else {
                tempArr[third++] = k[mid++];
            }
        }

        // 剩余部分依次放入中间数组
        while (mid <= right) {
            tempArr[third++] = k[mid++];
        }

        while (left <= center) {
            tempArr[third++] = k[left++];
        }
        // 将中间数组中的内容复制回原数组
        while (temp <= right) {
            k[temp] = tempArr[temp];
            temp++;
        }
    }

}

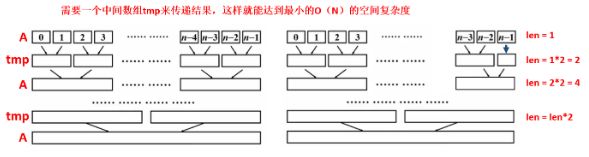
三、合并排序的非递归实现（迭代）