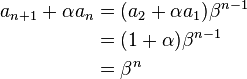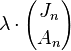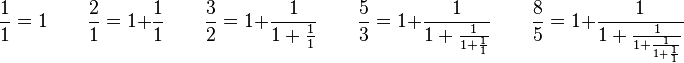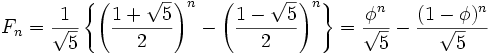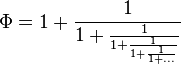斐波那契数列
转http://zh.wikipedia.org/wiki/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97
表达式
为求得斐波那契数列的一般表达式,可以借助线性代数的方法。高中的初等数学知识也能求出。
高中的初等数学知识解法
已知
- a1 = 1
- a2 = 1
- an = an − 1 + an − 2
1首先构建等比数列
设an + αan − 1 = β(an − 1 + αan − 2)
化简得
an = (β − α)an − 1 + αβan − 2
比较系数可得: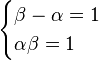
不妨设β > 0α > 0
解得:
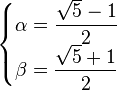
所以有an + αan − 1 = β(an − 1 + αan − 2) 即{an + αan − 1}为等比数列。
2求出数列{an + αan − 1}
3求数列{bn}进而得到{an}
![]()
设![]() 解得
解得![]() 故数列 bn + λ 为等比数列
故数列 bn + λ 为等比数列
即 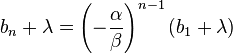 而
而 ![]() 故有
故有 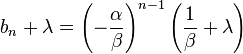
又有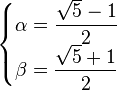 和
和 ![]()
可得 ![]()
得出 an 表达式
![]()
线性代数解法
1 首先构建一个矩阵方程
设Jn为第n个月新出生的兔子数量,An为这一月份的兔子数量。
上式表达了两个月之间,兔子数目之间的关系。而要求的是,An+1的表达式。
2 求矩阵的特征值: λ
行列式:-λ*(1-λ)-1*1=λ²-λ-1
3特征向量
将两个特征值代入
求特征向量![]() 得
得
4 分解首向量
第一个月的情况是兔子一对,新生0对。
将它分解为用特征向量表示。
5用数学归纳法证明
从
可得
6 化简矩阵方程
将(4) 代入 (5)
根据 3
7 求A的表达式
现在在6的基础上,可以很快求出An+1 的表达式,将两个特征值代入 6 中
(7)即为An+1 的表达式
近似值
用计算机求解
可通过编程观察斐波那契数列。分为两类问题,一种已知数列中的某一项,求序数。第二种是已知序数,求该项的值。
可通过递归的算法解决此两个问题。
和黄金分割的关系
开普勒发现两个斐波那契数的比会趋近黄金分割:
斐波那契数亦可以用连分数来表示:
而黄金分割数亦可以用无限连分数表示:
和自然的关系
许多的生物构成都和斐波那契数列有正相关。例如人体从肚脐至头顶之距离和从肚脐至脚底之距趋近于![]() 向日葵的种子螺旋排列99%是
向日葵的种子螺旋排列99%是![]() 。
。
恒等式
证明以下的恒等式有很多方法。以下会用组合论述来证明。Fn可以表示成用多个1和多个2相加令其和等于
- F1 + F2 + F3 + ... + Fn = Fn + 2 - 1
计算用多个1和多个2相加令其和等于n+1的方法的数目,同时最后一个加数是2的情况。
如前所述,当n ≥ 0,有Fn + 2种这样的方法。因为当中只有一种方法不用使用2,就即 1 + 1 + ... + 1 (n+1项),于是我们从Fn + 2减去1。
- 若第1个被加数是2,有Fn个方法来计算加至n-1的方法的数目;
- 若第2个被加数是2、第1个被加数是1,有Fn - 1个方法来计算加至n − 2的方法的数目。
- 重复以上动作。
- 若第n + 1个被加数为2,它之前的被加数均为1,就有F(0)个方法来计算加至0的数目。
若该数式包含2为被加数,2的首次出现位置必然在第1和n+1的被加数之间。2在不同位置的情况都考虑到后,得出Fn + Fn - 1 + ... + F0为要求的数目。
- F1 + 2F2 + 3F3 + ... + nFn = nFn + 2 - Fn + 3 + 2
- F1 + F3 + F5 + ... + F2n - 1 = F2n
- F2 + F4 + F6 + ... + F2n = F2n + 1 - 1
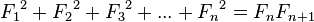
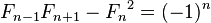
相关的数列
斐波那契数列是卢卡斯数列的特殊情况。或是斐波那契n步数列步数为2的情形。
和卢卡斯数列的关系
反斐波那契数列
反斐波那契数列的递归公式如下:
- Gn + 2 = Gn − Gn + 1
如果它以1,-1,之后的数是:1,-1,2,-3,5,-8, ...
即是F_{2n+1} = G_{2n+1},F_{2n} = - G_{2n}。
巴都万数列
斐波那契数列可以用一个接一个的正方形来表现,巴都万数列则是用一个接一个的等边三角形来表现,它有Pn = Pn − 2 + Pn − 3的关系。
应用
1970年,Yuri Matiyasevich 指出了偶角标的斐波那契函数
- y = F2x
正是满足 Julia Robison 假设的丢番图函数,因而证明了希尔伯特第十问题是不可解的。