Java学习day065 遗留的集合（Hashtable类、枚举、属性映射、栈、位集）

使用的教材是java核心技术卷1，我将跟着这本书的章节同时配合视频资源来进行学习基础java知识。

day065   遗留的集合（Hashtable类、枚举、属性映射、栈、位集）

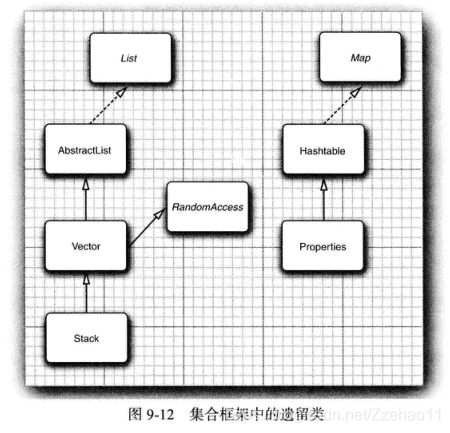
从Java第1版问世以来，在集合框架出现之前已经存在大量“遗留的”容器类。这些类已经集成到集合框架中，如图所示。

                                  

---

1.Hashtable类

Hashtable类与HashMap类的作用一样，实际上，它们拥有相同的接口。与Vector类的方法一样。Hashtable的方法也是同步的。如果对同步性或与遗留代码的兼容性没有任何要求，就应该使用HashMap。如果需要并发访问，则要使用ConcurrentHashMap。

---

2.枚举

遗留集合使用Enumeration接口对元素序列进行遍历。Enumeration接口有两个方法，即hasMoreElements和nextElement。这两个方法与Iterator接口的hasNext方法和next方法十分类似。

例如，Hashtable类的elements方法将产生一个用于描述表中各个枚举值的对象：

Enuineration e = staff.elements();
whi1e (e_HasMoreElements())
{
    Eniployee e = e.nextElement();
    ...
}

有时还会遇到遗留的方法，其参数是枚举类型的。静态方法Collections.enumeration将产生一个枚举对象，枚举集合中的元素。例如：

List streams = . . .;
Sequencel叩utStream in = new SequencelnputStream(Collections.enumeration(streams));
//the SequencelnputStream constructor expects an enumeration

                      

---

3.属性映射

属性映射（propertymap)是一个类型非常特殊的映射结构。它有下面3个特性：

•键与值都是字符串。

•表可以保存到一个文件中，也可以从文件中加载。

•使用一个默认的辅助表。

实现属性映射的Java平台类称为Properties。

  

---

4.栈

从1.0版开始，标准类库中就包含了Stack类，其中有大家熟悉的push方法和pop方法。但是，Stack类扩展为Vector类，从理论角度看，Vector类并不太令人满意，它可以让栈使用不属于栈操作的insert和remove方法，即可以在任何地方进行插入或删除操作，而不仅仅是在栈顶。

---

5.位集

Java平台的BitSet类用于存放一个位序列（它不是数学上的集，称为位向量或位数组更为合适)。如果需要高效地存储位序列（例如，标志）就可以使用位集。由于位集将位包装在字节里，所以，使用位集要比使用Boolean对象的ArrayList更加高效。

BitSet类提供了一个便于读取、设置或清除各个位的接口。使用这个接口可以避免屏蔽和其他麻烦的位操作。如果将这些位存储在int或long变量中就必须进行这些繁琐的操作。

例如，对于一个名为bucketOfBits的BitSet,

bucketOfBits.get(i)

如果第i位处于“开”状态，就返回true;否则返回false。同样地，

bucketOfBits.set(i)

将第i位置为“开”状态。最后，

bucketOfBits.clear(i)

将第i位置为“关”状态。

  

作为位集应用的一个示例，这里给出一个采用“Eratosthenes筛子”算法查找素数的实现（素数是指只能被1和本身整除的数，例如2、3或5,“Eratosthenes筛子”算法是最早发现的用来枚举这些基本数字的方法之一)。这并不是一种查找素数的最好方法，但是由于某种原因，它已经成为测试编译程序性能的一种流行的基准。（这也不是一种最好的基准测试方法，它主要用于测试位操作。）

在此，将尊重这个传统，并给出实现。其程序将计算2-2000000之间的所有素数（一共有148933个素数，或许不打算把它们全部打印出来吧)。

这里并不想深人程序的细节，关键是要遍历一个拥有200万个位的位集。首先将所有的位置为“开”状态，然后，将已知素数的倍数所对应的位都置为“关”状态。经过这个操作保留下来的位对应的就是素数。

下面的程序实现这个算法：

/**
 *@author  zzehao
 */
import java.util.*;

public class Sieve
{
	public static void main(String[] s)
	{
		int n = 2000000;
		long start = System.currentTimeMillis();
		BitSet b = new BitSet(n+1 );
		int count = 0;
		int i;
		for (i = 2;i<= n;i++)
			b.set(i);
		i = 2;
		while (i*i <= n)
		{
			if (b.get(i))
			{
				count++;
				int k = 2*i;
				while (k <= n)
				{
					b.clear(k);
					k+=i;
				}
			}
			i++;
		}
		while (i<=n)
		{
			if(b.get(i)) count++;
			i++;
		}
		long end = System.currentTimeMillis();
		System.out.println(count+ "primes");
		System.out.println((end - start)+ " milliseconds");
	}
}

 

运行的结果：

     

---