DP - 树形DP - 战略游戏 + 皇宫看守
DP - 树形DP - 战略游戏 + 皇宫看守
文章目录
-
- DP - 树形DP - 战略游戏 + 皇宫看守
-
- 1、战略游戏
- 2、皇宫看守
1、战略游戏
鲍勃喜欢玩电脑游戏,特别是战略游戏,但有时他找不到解决问题的方法,这让他很伤心。
现在他有以下问题。
他必须保护一座中世纪城市,这条城市的道路构成了一棵树。
每个节点上的士兵可以观察到所有和这个点相连的边。
他必须在节点上放置最少数量的士兵,以便他们可以观察到所有的边。
你能帮助他吗?
例如,下面的树:
只需要放置1名士兵(在节点1处),就可观察到所有的边。
输入格式
输入包含多组测试数据,每组测试数据用以描述一棵树。
对于每组测试数据,第一行包含整数N,表示树的节点数目。
接下来N行,每行按如下方法描述一个节点。
节点编号:(子节点数目) 子节点 子节点 …
节点编号从0到N-1,每个节点的子节点数量均不超过10,每个边在输入数据中只出现一次。
输出格式
对于每组测试数据,输出一个占据一行的结果,表示最少需要的士兵数。
数据范围 分析: 抽 象 地 , 本 题 是 要 在 一 棵 树 中 选 择 尽 量 少 的 点 , 使 得 每 条 边 上 至 少 选 择 了 一 个 点 。 求 最 少 需 要 选 择 多 少 个 点 。 抽象地,本题是要在一棵树中选择尽量少的点,使得每条边上至少选择了一个点。\\求最少需要选择多少个点。 抽象地,本题是要在一棵树中选择尽量少的点,使得每条边上至少选择了一个点。求最少需要选择多少个点。 与 与 与——《Anniversary party - POJ - 2342》 类 似 , 该 题 是 每 条 边 至 多 选 择 一 点 , 本 题 是 每 条 表 至 少 选 择 一 点 。 类似,该题是每条边至多选择一点,本题是每条表至少选择一点。 类似,该题是每条边至多选择一点,本题是每条表至少选择一点。 状 态 表 示 , f [ i , 0 ] : 表 示 不 选 择 节 点 i 所 需 的 点 的 数 量 的 最 小 值 。 f [ i , 1 ] : 表 示 选 择 节 点 i 所 需 的 点 的 数 量 的 最 小 值 。 状态表示,\\f[i,0]:表示不选择节点i所需的点的数量的最小值。\\f[i,1]:表示选择节点i所需的点的数量的最小值。 状态表示,f[i,0]:表示不选择节点i所需的点的数量的最小值。f[i,1]:表示选择节点i所需的点的数量的最小值。 状 态 计 算 : ① 、 若 不 选 择 节 点 i , 则 必 须 选 择 i 的 孩 子 节 点 j , 即 f [ i , 0 ] + = f [ j , 1 ] 。 状态计算:\\①、若不选择节点i,则必须选择i的孩子节点j,即f[i,0]+=f[j,1]。 状态计算:①、若不选择节点i,则必须选择i的孩子节点j,即f[i,0]+=f[j,1]。 另外: 由 于 是 有 向 图 , 需 要 从 根 节 点 进 入 搜 索 。 由于是有向图,需要从根节点进入搜索。 由于是有向图,需要从根节点进入搜索。 代码: 太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。 皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中结点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。 已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。 大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。 可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。 帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。 输入格式 第一行 n,表示树中结点的数目。 第二行至第 n+1 行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 i,在该宫殿安置侍卫所需的经费 k,该结点的子结点数 m,接下来 m 个数,分别是这个结点的 m 个子结点的标号 r1,r2,…,rm。 对于一个 n 个结点的树,结点标号在 1 到 n 之间,且标号不重复。 输出格式 数据范围 样例解释: 分析: 本 题 与 第 一 题 类 似 , 本 题 需 要 保 证 每 个 节 点 和 与 该 节 点 直 接 相 邻 的 节 点 中 , 至 少 选 择 一 个 点 。 选 择 每 个 节 点 需 要 一 定 的 花 费 , 要 求 最 小 花 费 。 本题与第一题类似,\\本题需要保证每个节点和与该节点直接相邻的节点中,至少选择一个点。\\选择每个节点需要一定的花费,要求最小花费。 本题与第一题类似,本题需要保证每个节点和与该节点直接相邻的节点中,至少选择一个点。选择每个节点需要一定的花费,要求最小花费。 样例: 这 样 对 每 个 节 点 u 来 说 有 三 种 情 况 : 这样对每个节点u来说有三种情况: 这样对每个节点u来说有三种情况: ① 、 u 节 点 由 父 节 点 看 守 , 那 么 可 以 选 择 u , 也 可 以 不 选 择 u 。 若 不 选 择 u , 则 必 选 择 u 的 孩 子 j 。 即 f [ u , 0 ] + = m i n ( f [ j , 1 ] , f [ j , 2 ] ) 。 ①、u节点由父节点看守,那么可以选择u,也可以不选择u。若不选择u,则必选择u的孩子j。\\\qquad即f[u,0]+=min(f[j,1],f[j,2])。 ①、u节点由父节点看守,那么可以选择u,也可以不选择u。若不选择u,则必选择u的孩子j。即f[u,0]+=min(f[j,1],f[j,2])。 ② 、 u 节 点 由 自 己 看 守 , 则 u 的 孩 子 节 点 选 不 选 均 可 。 若 不 选 , 则 必 选 择 j 的 孩 子 。 即 f [ u , 2 ] + = m i n ( f [ j , 0 ] , f [ j , 1 ] , f [ j , 2 ] ) 。 ②、u节点由自己看守,则u的孩子节点选不选均可。若不选,则必选择j的孩子。\\\qquad即f[u,2]+=min(f[j,0],f[j,1],f[j,2])。 ②、u节点由自己看守,则u的孩子节点选不选均可。若不选,则必选择j的孩子。即f[u,2]+=min(f[j,0],f[j,1],f[j,2])。 ③ 、 u 节 点 由 孩 子 节 点 看 守 , 则 需 考 虑 由 哪 个 孩 子 节 点 看 守 的 花 费 最 低 , 总 花 费 应 当 是 选 择 孩 子 j 看 守 的 花 费 f [ j , 2 ] + 选 择 其 他 孩 子 的 最 小 花 费 。 u 所 有 孩 子 被 看 守 到 的 方 案 当 中 的 最 小 花 费 是 ∑ m i n ( f [ j , 1 ] , f [ j , 2 ] ) , 选 择 第 j 个 孩 子 后 , 其 他 孩 子 的 最 小 花 费 就 是 ∑ m i n ( f [ j , 1 ] , f [ j , 2 ] ) − f [ j , 2 ] 。 而 ∑ m i n ( f [ j , 1 ] , f [ j , 2 ] ) 在 第 ① 步 已 被 计 算 出 来 了 , 就 是 f [ u , 0 ] , 故 总 的 最 小 花 费 应 为 f [ u ] [ 1 ] = m i n ( f [ u ] [ 1 ] , f [ j ] [ 2 ] + f [ u ] [ 0 ] − m i n ( f [ j ] [ 1 ] , f [ j ] [ 2 ] ) ) 。 ③、u节点由孩子节点看守,则需考虑由哪个孩子节点看守的花费最低,\\ \ \\\qquad总花费应当是选择孩子j看守的花费f[j,2]+选择其他孩子的最小花费。\\ \ \\\qquad u所有孩子被看守到的方案当中的最小花费是\sum min(f[j,1],f[j,2]),\\ \ \\\qquad选择第j个孩子后,其他孩子的最小花费就是\sum min(f[j,1],f[j,2])-f[j,2]。\\ \ \\\qquad而\sum min(f[j,1],f[j,2])在第①步已被计算出来了,就是f[u,0],\\ \ \\\qquad故总的最小花费应为f[u][1]=min(f[u][1],f[j][2]+f[u][0]-min(f[j][1],f[j][2]))。 ③、u节点由孩子节点看守,则需考虑由哪个孩子节点看守的花费最低, 总花费应当是选择孩子j看守的花费f[j,2]+选择其他孩子的最小花费。 u所有孩子被看守到的方案当中的最小花费是∑min(f[j,1],f[j,2]), 选择第j个孩子后,其他孩子的最小花费就是∑min(f[j,1],f[j,2])−f[j,2]。 而∑min(f[j,1],f[j,2])在第①步已被计算出来了,就是f[u,0], 故总的最小花费应为f[u][1]=min(f[u][1],f[j][2]+f[u][0]−min(f[j][1],f[j][2]))。 代码:
0输入样例:
4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
输出样例:
1
2
② 、 若 选 择 节 点 i , 则 可 选 孩 子 j 也 可 不 选 , 即 f [ i , 0 ] + = m i n ( f [ j , 0 ] , f [ j , 1 ] ) 。 ②、若选择节点i,则可选孩子j也可不选,即f[i,0]+=min(f[j,0],f[j,1])。 ②、若选择节点i,则可选孩子j也可不选,即f[i,0]+=min(f[j,0],f[j,1])。#include
2、皇宫看守
输入中数据描述一棵树,描述如下:
输出一个整数,表示最少的经费。
1≤n≤1500输入样例:
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
输出样例:
25
在2、3、4结点安排护卫,可以观察到全部宫殿,所需经费最少,为 16 + 5 + 4 = 25。
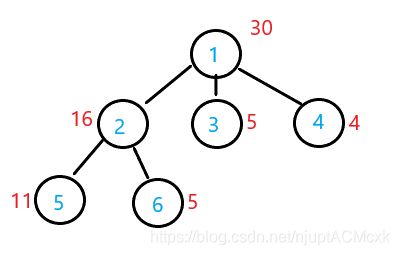
状 态 表 示 , f [ u , 0 ] : 节 点 u 由 父 节 点 看 守 。 状态表示,\\f[u,0]:节点u由父节点看守。 状态表示,f[u,0]:节点u由父节点看守。
f [ u , 1 ] : 节 点 u 由 孩 子 节 点 看 守 。 f[u,1]:节点u由孩子节点看守。 f[u,1]:节点u由孩子节点看守。
f [ u , 2 ] : 节 点 u 由 自 己 看 守 。 f[u,2]:节点u由自己看守。 f[u,2]:节点u由自己看守。#include
