LCCUP 力扣杯2020秋季编程大赛题解
目录
1. 速算机器人
2. 早餐组合
3. 秋叶收藏集
4. 快速公交
5. 追逐游戏
1. 速算机器人
小扣在秋日市集发现了一款速算机器人。店家对机器人说出两个数字(记作 x 和 y),请小扣说出计算指令:
"A"运算:使x = 2 * x + y;"B"运算:使y = 2 * y + x。
在本次游戏中,店家说出的数字为 x = 1 和 y = 0,小扣说出的计算指令记作仅由大写字母 A、B 组成的字符串 s,字符串中字符的顺序表示计算顺序,请返回最终 x 与 y 的和为多少。
示例 1:
输入:
s = "AB"输出:
4解释:
经过一次 A 运算后,x = 2, y = 0。
再经过一次 B 运算,x = 2, y = 2。
最终 x 与 y 之和为 4。
提示:
0 <= s.length <= 10s由'A'和'B'组成
解题思路:
直接便利一遍字符串,按照题意直接进行计算
代码:
class Solution {
public:
int calculate(string s) {
int x = 1,y = 0;
for(int i = 0;i2. 早餐组合
小扣在秋日市集选择了一家早餐摊位,一维整型数组 staple 中记录了每种主食的价格,一维整型数组 drinks 中记录了每种饮料的价格。小扣的计划选择一份主食和一款饮料,且花费不超过 x 元。请返回小扣共有多少种购买方案。
注意:答案需要以 1e9 + 7 (1000000007) 为底取模,如:计算初始结果为:1000000008,请返回 1
示例 1:
输入:
staple = [10,20,5], drinks = [5,5,2], x = 15输出:
6解释:小扣有 6 种购买方案,所选主食与所选饮料在数组中对应的下标分别是:
第 1 种方案:staple[0] + drinks[0] = 10 + 5 = 15;
第 2 种方案:staple[0] + drinks[1] = 10 + 5 = 15;
第 3 种方案:staple[0] + drinks[2] = 10 + 2 = 12;
第 4 种方案:staple[2] + drinks[0] = 5 + 5 = 10;
第 5 种方案:staple[2] + drinks[1] = 5 + 5 = 10;
第 6 种方案:staple[2] + drinks[2] = 5 + 2 = 7。
示例 2:
输入:
staple = [2,1,1], drinks = [8,9,5,1], x = 9输出:
8解释:小扣有 8 种购买方案,所选主食与所选饮料在数组中对应的下标分别是:
第 1 种方案:staple[0] + drinks[2] = 2 + 5 = 7;
第 2 种方案:staple[0] + drinks[3] = 2 + 1 = 3;
第 3 种方案:staple[1] + drinks[0] = 1 + 8 = 9;
第 4 种方案:staple[1] + drinks[2] = 1 + 5 = 6;
第 5 种方案:staple[1] + drinks[3] = 1 + 1 = 2;
第 6 种方案:staple[2] + drinks[0] = 1 + 8 = 9;
第 7 种方案:staple[2] + drinks[2] = 1 + 5 = 6;
第 8 种方案:staple[2] + drinks[3] = 1 + 1 = 2;
提示:
1 <= staple.length <= 10^51 <= drinks.length <= 10^51 <= staple[i],drinks[i] <= 10^51 <= x <= 2*10^5
解题思路:
首先对两个数组进行排序,然后遍历第一个数组的每一个数,然后用x减去该数,在另一个数组中进行二分查找,就能找到在满足第一个数组值的同时,第二个数组中满足的个数,求和即可
代码:
class Solution {
public:
const int mod = 1e9+7;
int breakfastNumber(vector& staple, vector& drinks, int x) {
sort(staple.begin(),staple.end());
sort(drinks.begin(),drinks.end());
long long ans = 0;
for(int i = 0;ix)break;
int idx = lower_bound(drinks.begin(),drinks.end(),x-s+1)-drinks.begin();
if(idx==0)continue;
ans = (ans+idx)%mod;
}
return ans;
}
}; 3. 秋叶收藏集
小扣出去秋游,途中收集了一些红叶和黄叶,他利用这些叶子初步整理了一份秋叶收藏集 leaves, 字符串 leaves 仅包含小写字符 r 和 y, 其中字符 r 表示一片红叶,字符 y 表示一片黄叶。
出于美观整齐的考虑,小扣想要将收藏集中树叶的排列调整成「红、黄、红」三部分。每部分树叶数量可以不相等,但均需大于等于 1。每次调整操作,小扣可以将一片红叶替换成黄叶或者将一片黄叶替换成红叶。请问小扣最少需要多少次调整操作才能将秋叶收藏集调整完毕。
示例 1:
输入:
leaves = "rrryyyrryyyrr"输出:
2解释:调整两次,将中间的两片红叶替换成黄叶,得到 "rrryyyyyyyyrr"
示例 2:
输入:
leaves = "ryr"输出:
0解释:已符合要求,不需要额外操作
提示:
3 <= leaves.length <= 10^5leaves中只包含字符'r'和字符'y'
解题思路:
借鉴这里的说法,用 s[x] 表示 [0, x) 区间内红叶的数量. 假设整理后红叶的区间为 [0, i] 和 [j, n), 那么黄叶的区间为 [i+1, j), 需要操作的总次数为 (i + 1 - s[i + 1]) + (n - j - s[n] + s[j]) + (s[j] - s[i + 1]), 整理后得到 n - s[n] + (i - 2 * s[i]) - (j - 2 * s[j]), 只需要记录到目前为止看到的 x - 2 * s[x] 的最小值即可,因此令s[x] = x - 2 * s[x],结果ans=min(ans,s[n] + s[i] - j)
代码:
class Solution {
public:
int minimumOperations(string leaves) {
int n = leaves.size();
int ans = 1e9;
vectors(n+1,0);
for(int i = 0;i 4. 快速公交
小扣打算去秋日市集,由于游客较多,小扣的移动速度受到了人流影响:
- 小扣从
x号站点移动至x + 1号站点需要花费的时间为inc; - 小扣从
x号站点移动至x - 1号站点需要花费的时间为dec。
现有 m 辆公交车,编号为 0 到 m-1。小扣也可以通过搭乘编号为 i 的公交车,从 x 号站点移动至 jump[i]*x 号站点,耗时仅为 cost[i]。小扣可以搭乘任意编号的公交车且搭乘公交次数不限。
假定小扣起始站点记作 0,秋日市集站点记作 target,请返回小扣抵达秋日市集最少需要花费多少时间。由于数字较大,最终答案需要对 1000000007 (1e9 + 7) 取模。
注意:小扣可在移动过程中到达编号大于 target 的站点。
示例 1:
输入:
target = 31, inc = 5, dec = 3, jump = [6], cost = [10]输出:
33解释:
小扣步行至 1 号站点,花费时间为 5;
小扣从 1 号站台搭乘 0 号公交至 6 * 1 = 6 站台,花费时间为 10;
小扣从 6 号站台步行至 5 号站台,花费时间为 3;
小扣从 5 号站台搭乘 0 号公交至 6 * 5 = 30 站台,花费时间为 10;
小扣从 30 号站台步行至 31 号站台,花费时间为 5;
最终小扣花费总时间为 33。
示例 2:
输入:
target = 612, inc = 4, dec = 5, jump = [3,6,8,11,5,10,4], cost = [4,7,6,3,7,6,4]输出:
26解释:
小扣步行至 1 号站点,花费时间为 4;
小扣从 1 号站台搭乘 0 号公交至 3 * 1 = 3 站台,花费时间为 4;
小扣从 3 号站台搭乘 3 号公交至 11 * 3 = 33 站台,花费时间为 3;
小扣从 33 号站台步行至 34 站台,花费时间为 4;
小扣从 34 号站台搭乘 0 号公交至 3 * 34 = 102 站台,花费时间为 4;
小扣从 102 号站台搭乘 1 号公交至 6 * 102 = 612 站台,花费时间为 7;
最终小扣花费总时间为 26。
提示:
1 <= target <= 10^91 <= jump.length, cost.length <= 102 <= jump[i] <= 10^61 <= inc, dec, cost[i] <= 10^6
解题思路:
到达位置target可以分为先到位置【target/jump[i]】(下取整的意思),再经过一个jump[i],然后一步一步增加走到target,也可以先走到【target/jump[i]】+ 1位置,再经过jump[i],然后再一步一步减少到target,储存中间结果进行记忆化搜索
代码:
class Solution {
map mp;
const int mod = 1e9+7;
long long fun(int target, int inc, int dec,vector& jump, vector& cost)
{
if(target==0)return 0;
if(mp.count(target))return mp[target];
long long s=(long long)target*inc;
for(int i=0;i1&&target%jump[i])s=min(s,fun(target/jump[i]+1,inc, dec,jump, cost)+cost[i]+(long long)(jump[i]-target%jump[i])*dec);
}
return mp[target]=s;
}
public:
int busRapidTransit(int target, int inc, int dec, vector& jump, vector& cost) {
mp.clear();
return fun(target,inc, dec,jump, cost)%mod;
}
};
5. 追逐游戏
秋游中的小力和小扣设计了一个追逐游戏。他们选了秋日市集景区中的 N 个景点,景点编号为 1~N。此外,他们还选择了 N 条小路,满足任意两个景点之间都可以通过小路互相到达,且不存在两条连接景点相同的小路。整个游戏场景可视作一个无向连通图,记作二维数组 edges,数组中以 [a,b] 形式表示景点 a 与景点 b 之间有一条小路连通。
小力和小扣只能沿景点间的小路移动。小力的目标是在最快时间内追到小扣,小扣的目标是尽可能延后被小力追到的时间。游戏开始前,两人分别站在两个不同的景点 startA 和 startB。每一回合,小力先行动,小扣观察到小力的行动后再行动。小力和小扣在每回合可选择以下行动之一:
- 移动至相邻景点
- 留在原地
如果小力追到小扣(即两人于某一时刻出现在同一位置),则游戏结束。若小力可以追到小扣,请返回最少需要多少回合;若小力无法追到小扣,请返回 -1。
注意:小力和小扣一定会采取最优移动策略。
示例 1:
输入:
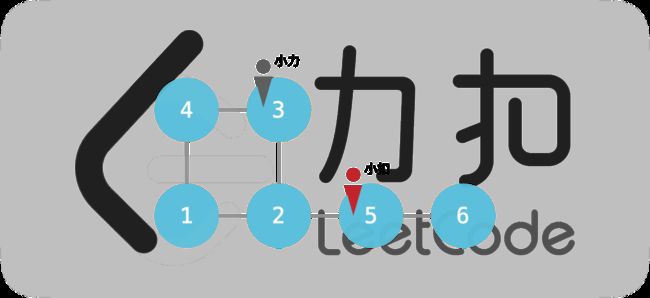
edges = [[1,2],[2,3],[3,4],[4,1],[2,5],[5,6]], startA = 3, startB = 5输出:
3第一回合,小力移动至 2 号点,小扣观察到小力的行动后移动至 6 号点;
第二回合,小力移动至 5 号点,小扣无法移动,留在原地;
第三回合,小力移动至 6 号点,小力追到小扣。返回 3。
示例 2:
输入:
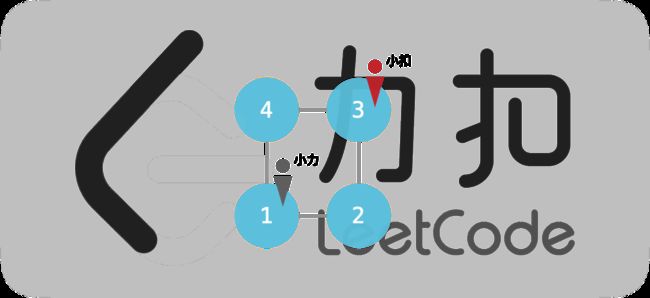
edges = [[1,2],[2,3],[3,4],[4,1]], startA = 1, startB = 3输出:
-1小力如果不动,则小扣也不动;否则小扣移动到小力的对角线位置。这样小力无法追到小扣。
提示:
edges的长度等于图中节点个数3 <= edges.length <= 10^51 <= edges[i][0], edges[i][1] <= edges.length 且 edges[i][0] != edges[i][1]1 <= startA, startB <= edges.length 且 startA != startB
解题思路:
代码: