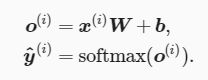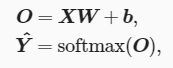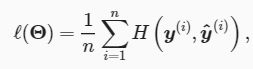[STAT-157] Softmax
课程Youtube:Deep Learning UC Berkeley STAT-157
课本:动手学深度学习
代码:d2l-ai
3.4. softmax回归
前几节介绍的线性回归模型适用于输出为连续值的情景。在另一类情景中,模型输出可以是一个像图像类别这样的离散值。对于这样的离散值预测问题,我们可以使用诸如softmax回归在内的分类模型。和线性回归不同,softmax回归的输出单元从一个变成了多个,且引入了softmax运算使输出更适合离散值的预测和训练。本节以softmax回归模型为例,介绍神经网络中的分类模型。
3.4.1. 分类问题
让我们考虑一个简单的图像分类问题,其输入图像的高和宽均为2像素,且色彩为灰度。这样每个像素值都可以用一个标量表示。我们将图像中的4像素分别记为![]() 。假设训练数据集中图像的真实标签为狗、猫或鸡(假设可以用4像素表示出这3种动物),这些标签分别对应离散值
。假设训练数据集中图像的真实标签为狗、猫或鸡(假设可以用4像素表示出这3种动物),这些标签分别对应离散值![]() 。
。
我们通常使用离散的数值来表示类别,例如![]() 。如此,一张图像的标签为1、2和3这3个数值中的一个。虽然我们仍然可以使用回归模型来进行建模,并将预测值就近定点化到1、2和3这3个离散值之一,但这种连续值到离散值的转化通常会影响到分类质量。因此我们一般使用更加适合离散值输出的模型来解决分类问题。
。如此,一张图像的标签为1、2和3这3个数值中的一个。虽然我们仍然可以使用回归模型来进行建模,并将预测值就近定点化到1、2和3这3个离散值之一,但这种连续值到离散值的转化通常会影响到分类质量。因此我们一般使用更加适合离散值输出的模型来解决分类问题。
3.4.2. softmax回归模型
softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于,softmax回归的输出值个数等于标签里的类别数。因为一共有4种特征和3种输出动物类别,所以权重包含12个标量(带下标的w)、偏差包含3个标量(带下标的b),且对每个输入计算![]() 这3个输出:
这3个输出:
图3.2用神经网络图描绘了上面的计算。softmax回归同线性回归一样,也是一个单层神经网络。由于每个输出![]() 的计算都要依赖于所有的输入
的计算都要依赖于所有的输入![]() ,softmax回归的输出层也是一个全连接层。
,softmax回归的输出层也是一个全连接层。
3.4.2.1. softmax运算
既然分类问题需要得到离散的预测输出,一个简单的办法是将输出值![]() 当作预测类别是i的置信度,并将值最大的输出所对应的类作为预测输出,即输出
当作预测类别是i的置信度,并将值最大的输出所对应的类作为预测输出,即输出![]() 。例如,如果
。例如,如果![]() 分别为
分别为![]() ,由于
,由于![]() 最大,那么预测类别为2,其代表猫。
最大,那么预测类别为2,其代表猫。
然而,直接使用输出层的输出有两个问题。一方面,由于输出层的输出值的范围不确定,我们难以直观上判断这些值的意义。例如,刚才举的例子中的输出值10表示“很置信”图像类别为猫,因为该输出值是其他两类的输出值的100倍。但如果![]() ,那么输出值10却又表示图像类别为猫的概率很低。另一方面,由于真实标签是离散值,这些离散值与不确定范围的输出值之间的误差难以衡量。
,那么输出值10却又表示图像类别为猫的概率很低。另一方面,由于真实标签是离散值,这些离散值与不确定范围的输出值之间的误差难以衡量。
softmax运算符(softmax operator)解决了以上两个问题。它通过下式将输出值变换成值为正且和为1的概率分布:
其中
容易看出![]() 且
且![]() ,因此
,因此![]() 是一个合法的概率分布。这时候,如果
是一个合法的概率分布。这时候,如果![]() ,不管
,不管![]() 和
和![]() 的值是多少,我们都知道图像类别为猫的概率是80%。此外,我们注意到
的值是多少,我们都知道图像类别为猫的概率是80%。此外,我们注意到
因此softmax运算不改变预测类别输出。
3.4.3. 单样本分类的矢量计算表达式
为了提高计算效率,我们可以将单样本分类通过矢量计算来表达。在上面的图像分类问题中,假设softmax回归的权重和偏差参数分别为
设高和宽分别为2个像素的图像样本ii的特征为
输出层的输出为
预测为狗、猫或鸡的概率分布为
softmax回归对样本ii分类的矢量计算表达式为
3.4.4. 小批量样本分类的矢量计算表达式
为了进一步提升计算效率,我们通常对小批量数据做矢量计算。广义上讲,给定一个小批量样本,其批量大小为n,输入个数(特征数)为d,输出个数(类别数)为q。设批量特征为![]() 。假设softmax回归的权重和偏差参数分别为
。假设softmax回归的权重和偏差参数分别为![]() 和
和![]() 。softmax回归的矢量计算表达式为
。softmax回归的矢量计算表达式为
其中的加法运算使用了广播机制,![]() 且这两个矩阵的第ii行分别为样本ii的输出
且这两个矩阵的第ii行分别为样本ii的输出![]() 和概率分布
和概率分布![]() 。
。
3.4.5. 交叉熵损失函数
前面提到,使用softmax运算后可以更方便地与离散标签计算误差。我们已经知道,softmax运算将输出变换成一个合法的类别预测分布。实际上,真实标签也可以用类别分布表达:对于样本ii,我们构造向量![]() ,使其第
,使其第![]() (样本ii类别的离散数值)个元素为1,其余为0。这样我们的训练目标可以设为使预测概率分布
(样本ii类别的离散数值)个元素为1,其余为0。这样我们的训练目标可以设为使预测概率分布![]() 尽可能接近真实的标签概率分布
尽可能接近真实的标签概率分布![]() 。
。
我们可以像线性回归那样使用平方损失函数![]() 。然而,想要预测分类结果正确,我们其实并不需要预测概率完全等于标签概率。例如,在图像分类的例子里,如果
。然而,想要预测分类结果正确,我们其实并不需要预测概率完全等于标签概率。例如,在图像分类的例子里,如果![]() ,那么我们只需要
,那么我们只需要![]() 比其他两个预测值
比其他两个预测值![]() 和
和![]() 大就行了。即使
大就行了。即使![]() 值为0.6,不管其他两个预测值为多少,类别预测均正确。而平方损失则过于严格,例如
值为0.6,不管其他两个预测值为多少,类别预测均正确。而平方损失则过于严格,例如![]() 比
比![]() 的损失要小很多,虽然两者都有同样正确的分类预测结果。
的损失要小很多,虽然两者都有同样正确的分类预测结果。
改善上述问题的一个方法是使用更适合衡量两个概率分布差异的测量函数。其中,交叉熵(cross entropy)是一个常用的衡量方法:
其中带下标的![]() 是向量
是向量![]() 中非0即1的元素,需要注意将它与样本i类别的离散数值,即不带下标的
中非0即1的元素,需要注意将它与样本i类别的离散数值,即不带下标的![]() 区分。在上式中,我们知道向量
区分。在上式中,我们知道向量![]() 中只有第
中只有第![]() 个元素
个元素![]() 为1,其余全为0,于是
为1,其余全为0,于是![]() 。也就是说,交叉熵只关心对正确类别的预测概率,因为只要其值足够大,就可以确保分类结果正确。当然,遇到一个样本有多个标签时,例如图像里含有不止一个物体时,我们并不能做这一步简化。但即便对于这种情况,交叉熵同样只关心对图像中出现的物体类别的预测概率。
。也就是说,交叉熵只关心对正确类别的预测概率,因为只要其值足够大,就可以确保分类结果正确。当然,遇到一个样本有多个标签时,例如图像里含有不止一个物体时,我们并不能做这一步简化。但即便对于这种情况,交叉熵同样只关心对图像中出现的物体类别的预测概率。
假设训练数据集的样本数为n,交叉熵损失函数定义为
其中![]() 代表模型参数。同样地,如果每个样本只有一个标签,那么交叉熵损失可以简写成
代表模型参数。同样地,如果每个样本只有一个标签,那么交叉熵损失可以简写成![]() 。从另一个角度来看,我们知道最小化
。从另一个角度来看,我们知道最小化![]() 等价于最大化
等价于最大化![]() ,即最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。
,即最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。
3.4.6. 模型预测及评价
在训练好softmax回归模型后,给定任一样本特征,就可以预测每个输出类别的概率。通常,我们把预测概率最大的类别作为输出类别。如果它与真实类别(标签)一致,说明这次预测是正确的。在之后“softmax回归的从零开始实现”一节的实验中,我们将使用准确率(accuracy)来评价模型的表现。它等于正确预测数量与总预测数量之比。
3.4.7. 小结
- softmax回归适用于分类问题。它使用softmax运算输出类别的概率分布。
- softmax回归是一个单层神经网络,输出个数等于分类问题中的类别个数。
- 交叉熵适合衡量两个概率分布的差异。
3.4.8. 练习
- 查阅资料,了解最大似然估计。它与最小化交叉熵损失函数有哪些异曲同工之妙?
3.6. softmax回归的从零开始实现
这一节我们来动手实现softmax回归。首先导入本节实现所需的包或模块。
In [1]:
%matplotlib inline import d2lzh as d2l from mxnet import autograd, nd
3.6.1. 获取和读取数据
我们将使用Fashion-MNIST数据集,并设置批量大小为256。
In [2]:
batch_size = 256 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
3.6.2. 初始化模型参数
跟线性回归中的例子一样,我们将使用向量表示每个样本。已知每个样本输入是高和宽均为28像素的图像。模型的输入向量的长度是28×28=78428×28=784:该向量的每个元素对应图像中每个像素。由于图像有10个类别,单层神经网络输出层的输出个数为10,因此softmax回归的权重和偏差参数分别为784×10784×10和1×101×10的矩阵。
In [3]:
num_inputs = 784 num_outputs = 10 W = nd.random.normal(scale=0.01, shape=(num_inputs, num_outputs)) b = nd.zeros(num_outputs)
同之前一样,我们要为模型参数附上梯度。
In [4]:
W.attach_grad() b.attach_grad()
3.6.3. 实现softmax运算
在介绍如何定义softmax回归之前,我们先描述一下对如何对多维NDArray按维度操作。在下面的例子中,给定一个NDArray矩阵X。我们可以只对其中同一列(axis=0)或同一行(axis=1)的元素求和,并在结果中保留行和列这两个维度(keepdims=True)。
In [5]:
X = nd.array([[1, 2, 3], [4, 5, 6]]) X.sum(axis=0, keepdims=True), X.sum(axis=1, keepdims=True)
Out[5]:
( [[5. 7. 9.]], [[ 6.] [15.]] )
下面我们就可以定义前面小节里介绍的softmax运算了。在下面的函数中,矩阵X的行数是样本数,列数是输出个数。为了表达样本预测各个输出的概率,softmax运算会先通过exp函数对每个元素做指数运算,再对exp矩阵同行元素求和,最后令矩阵每行各元素与该行元素之和相除。这样一来,最终得到的矩阵每行元素和为1且非负。因此,该矩阵每行都是合法的概率分布。softmax运算的输出矩阵中的任意一行元素代表了一个样本在各个输出类别上的预测概率。
In [6]:
def softmax(X):
X_exp = X.exp()
partition = X_exp.sum(axis=1, keepdims=True)
return X_exp / partition # 这里应用了广播机制
可以看到,对于随机输入,我们将每个元素变成了非负数,且每一行和为1。
In [7]:
X = nd.random.normal(shape=(2, 5)) X_prob = softmax(X) X_prob, X_prob.sum(axis=1)
Out[7]:
( [[0.21324193 0.33961776 0.1239742 0.27106097 0.05210521] [0.11462264 0.3461234 0.19401033 0.29583326 0.04941036]], [1.0000001 1. ] )
3.6.4. 定义模型
有了softmax运算,我们可以定义上节描述的softmax回归模型了。这里通过reshape函数将每张原始图像改成长度为num_inputs的向量。
In [8]:
def net(X):
return softmax(nd.dot(X.reshape((-1, num_inputs)), W) + b)
3.6.5. 定义损失函数
上一节中,我们介绍了softmax回归使用的交叉熵损失函数。为了得到标签的预测概率,我们可以使用pick函数。在下面的例子中,变量y_hat是2个样本在3个类别的预测概率,变量y是这2个样本的标签类别。通过使用pick函数,我们得到了2个样本的标签的预测概率。与“softmax回归”一节数学表述中标签类别离散值从1开始逐一递增不同,在代码中,标签类别的离散值是从0开始逐一递增的。
In [9]:
y_hat = nd.array([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]]) y = nd.array([0, 2], dtype='int32') nd.pick(y_hat, y)
Out[9]:
[0.1 0.5]
下面实现了“softmax回归”一节中介绍的交叉熵损失函数。
In [10]:
def cross_entropy(y_hat, y):
return - nd.pick(y_hat, y).log()
3.6.6. 计算分类准确率
给定一个类别的预测概率分布y_hat,我们把预测概率最大的类别作为输出类别。如果它与真实类别y一致,说明这次预测是正确的。分类准确率即正确预测数量与总预测数量之比。
为了演示准确率的计算,下面定义准确率accuracy函数。其中y_hat.argmax(axis=1)返回矩阵y_hat每行中最大元素的索引,且返回结果与变量y形状相同。我们在“数据操作”一节介绍过,相等条件判断式(y_hat.argmax(axis=1) == y)是一个值为0(相等为假)或1(相等为真)的NDArray。由于标签类型为整数,我们先将变量y变换为浮点数再进行相等条件判断。
In [11]:
def accuracy(y_hat, y):
return (y_hat.argmax(axis=1) == y.astype('float32')).mean().asscalar()
让我们继续使用在演示pick函数时定义的变量y_hat和y,并将它们分别作为预测概率分布和标签。可以看到,第一个样本预测类别为2(该行最大元素0.6在本行的索引为2),与真实标签0不一致;第二个样本预测类别为2(该行最大元素0.5在本行的索引为2),与真实标签2一致。因此,这两个样本上的分类准确率为0.5。
In [12]:
accuracy(y_hat, y)
Out[12]:
0.5
类似地,我们可以评价模型net在数据集data_iter上的准确率。
In [13]:
# 本函数已保存在d2lzh包中方便以后使用。该函数将被逐步改进:它的完整实现将在“图像增广”一节中
# 描述
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
y = y.astype('float32')
acc_sum += (net(X).argmax(axis=1) == y).sum().asscalar()
n += y.size
return acc_sum / n
因为我们随机初始化了模型net,所以这个随机模型的准确率应该接近于类别个数10的倒数0.1。
In [14]:
evaluate_accuracy(test_iter, net)
Out[14]:
0.0925
3.6.7. 训练模型
训练softmax回归的实现跟“线性回归的从零开始实现”一节介绍的线性回归中的实现非常相似。我们同样使用小批量随机梯度下降来优化模型的损失函数。在训练模型时,迭代周期数num_epochs和学习率lr都是可以调的超参数。改变它们的值可能会得到分类更准确的模型。
In [15]:
num_epochs, lr = 5, 0.1
# 本函数已保存在d2lzh包中方便以后使用
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params=None, lr=None, trainer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
with autograd.record():
y_hat = net(X)
l = loss(y_hat, y).sum()
l.backward()
if trainer is None:
d2l.sgd(params, lr, batch_size)
else:
trainer.step(batch_size) # “softmax回归的简洁实现”一节将用到
y = y.astype('float32')
train_l_sum += l.asscalar()
train_acc_sum += (y_hat.argmax(axis=1) == y).sum().asscalar()
n += y.size
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size,
[W, b], lr)
epoch 1, loss 0.7886, train acc 0.746, test acc 0.793 epoch 2, loss 0.5745, train acc 0.811, test acc 0.821 epoch 3, loss 0.5289, train acc 0.823, test acc 0.830 epoch 4, loss 0.5053, train acc 0.831, test acc 0.833 epoch 5, loss 0.4897, train acc 0.835, test acc 0.839
3.6.8. 预测
训练完成后,现在就可以演示如何对图像进行分类了。给定一系列图像(第三行图像输出),我们比较一下它们的真实标签(第一行文本输出)和模型预测结果(第二行文本输出)。
In [16]:
for X, y in test_iter:
break
true_labels = d2l.get_fashion_mnist_labels(y.asnumpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1).asnumpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])
3.6.9. 小结
- 可以使用softmax回归做多类别分类。与训练线性回归相比,你会发现训练softmax回归的步骤和它非常相似:获取并读取数据、定义模型和损失函数并使用优化算法训练模型。事实上,绝大多数深度学习模型的训练都有着类似的步骤。
3.6.10. 练习
- 在本节中,我们直接按照softmax运算的数学定义来实现softmax函数。这可能会造成什么问题?(提示:试一试计算exp(50)exp(50)的大小。)
- 本节中的
cross_entropy函数是按照“softmax回归”一节中的交叉熵损失函数的数学定义实现的。这样的实现方式可能有什么问题?(提示:思考一下对数函数的定义域。) - 你能想到哪些办法来解决上面的两个问题?
3.7. softmax回归的简洁实现
我们在“线性回归的简洁实现”一节中已经了解了使用Gluon实现模型的便利。下面,让我们再次使用Gluon来实现一个softmax回归模型。首先导入所需的包或模块。
In [1]:
%matplotlib inline import d2lzh as d2l from mxnet import gluon, init from mxnet.gluon import loss as gloss, nn
3.7.1. 获取和读取数据
我们仍然使用Fashion-MNIST数据集和上一节中设置的批量大小。
In [2]:
batch_size = 256 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
3.7.2. 定义和初始化模型
在“softmax回归”一节中提到,softmax回归的输出层是一个全连接层。因此,我们添加一个输出个数为10的全连接层。我们使用均值为0、标准差为0.01的正态分布随机初始化模型的权重参数。
In [3]:
net = nn.Sequential() net.add(nn.Dense(10)) net.initialize(init.Normal(sigma=0.01))
3.7.3. softmax和交叉熵损失函数
如果做了上一节的练习,那么你可能意识到了分开定义softmax运算和交叉熵损失函数可能会造成数值不稳定。因此,Gluon提供了一个包括softmax运算和交叉熵损失计算的函数。它的数值稳定性更好。
In [4]:
loss = gloss.SoftmaxCrossEntropyLoss()
3.7.4. 定义优化算法
我们使用学习率为0.1的小批量随机梯度下降作为优化算法。
In [5]:
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.1})
3.7.5. 训练模型
接下来,我们使用上一节中定义的训练函数来训练模型。
In [6]:
num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None,
None, trainer)
epoch 1, loss 0.7886, train acc 0.747, test acc 0.805 epoch 2, loss 0.5730, train acc 0.812, test acc 0.825 epoch 3, loss 0.5295, train acc 0.824, test acc 0.823 epoch 4, loss 0.5054, train acc 0.831, test acc 0.835 epoch 5, loss 0.4892, train acc 0.834, test acc 0.838
3.7.6. 小结
- Gluon提供的函数往往具有更好的数值稳定性。
- 可以使用Gluon更简洁地实现softmax回归。
3.7.7. 练习
- 尝试调一调超参数,如批量大小、迭代周期和学习率,看看结果会怎样。
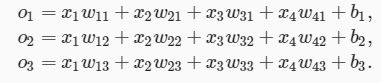
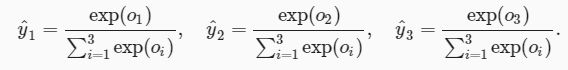
![[STAT-157] Softmax_第1张图片](http://img.e-com-net.com/image/info8/dc1269044c32400f919f195c672ab025.jpg)