动态规划(1)最长公共子序列

以前把大部分动态规划算法用java实现了遍，后来发现与python比代码行数太多，而python类似于伪代码，更容易一眼看出算法的核心，特此重新用python写一遍，方便快速了解算法。

最长公共子序列问题就是求序列A= a1,a2,……an , 和B = b1,b2,……bm ,的一个最长公共子序列。

暴力枚举

如果采用暴力枚举，只对A和B长度相同的子序列进行比较，那么忽略空序列，我们来看看：对于A长度为1的子序列有C(n,1)个，长度为2的子序列有C(n,2)个，……长度为n的子序列有C(n,n)个。对于B也可以做类似分析，即使只对序列A和序列B长度相同的子序列做比较，那么总的比较次数高达：

C(n,1)* C(m,1) *1 + C(n,2) * C(m,2) * 2+ …+C(n,p) * C(m,p)*p
p=min(m,n)

取m=n=100试一下，一个明显的下界即C(100,0)+C(100,1)+…+C(100,99)+C(100,100)= 2100 ，算到死都算不出。

DP

我们用Ax表示序列A的连续前x项构成的子序列，即Ax= a1,a2,……ax , By= b1,b2,……by , 我们用LCS(x, y)表示它们的最长公共子序列长度，那原问题等价于求LCS(m,n)。为了方便我们用L(x, y)表示Ax和By的一个最长公共子序列。
让我们来看看如何求LCS(x, y)。我们令x表示子序列考虑最后一项

Ax ＝ By

很显然，当Ax=By，LCS(x, y)=LCS(x-1, y-1)+1

Ax ≠ By

假设t是Ax与By的公共子串，由于Ax ≠ By，所以t不等于Ax或者也不等于By，这两个不等于至少成立一个。假如t≠Ax,那么有L(x, y)= L(x - 1, y)；如果假如t≠Bx,那么有L(x, y)= L(x , y-1).

综上得到结论，如果Ax ＝ By，L(x, y)==LCS(x-1, y-1)+1，否则L(x, y)=max(L(x-1,y),L(x,y-1))

这样可以得到最大子序列长度L(x,y)，那如何得到这个最大子序列呢。
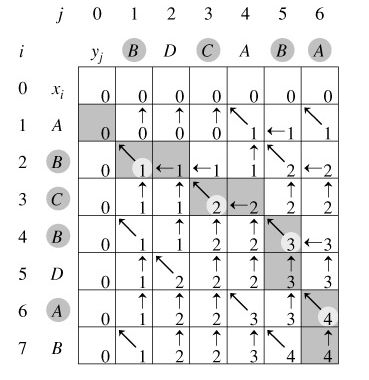
初始化一个矩阵L(m+1,n+1),其中L[0,:] 与 L[:,0]均等于0，代表与一个空串求LCS，很显然为0.假如对s1=”BDCABA”和s2=“ABCBDAB”求LCS，可以得到如下图：

很显然只要从二维数组最后一个元素出发，找到标记为斜箭头的元素输出，然后向左上角方向查找，直到元素为1为止，然后将找到的元素逆序即可找到最长子序列。

时间复杂度时O(n * m)，空间也是O(n * m)。其中回溯构造最优解的过程与传统不同，这里花费了额外线性空间tag，每一次只往左上角找,这里时间复杂度只需O(min(m,n)),传统是对左边或者上边找，需要O(m+n)。

s1=input()
s2=input()
ans=[]
ls1=len(s1)+1
ls2=len(s2)+1
A=[[0]*ls2 for i in range(ls1)]
tag=[]#用来标记斜箭头，例如5,6:4:'A'表示第5行 6列有公共字符‘A’LCS长度为4
for i in range(1,ls1):
    for j in range(1,ls2):
        if s1[i-1]!=s2[j-1]:
            A[i][j]=max(A[i-1][j],A[i][j-1])
        else:
            A[i][j]=A[i-1][j-1]+1
            tag.append((i,j,A[i][j],s2[j-1]))
ans=[]
goal=A[-1][-1] #最长子序列长度值
for t in reversed(tag):
    if t[0]and t[1]and t[2]==goal:
        ans.append(t[3])
        goal=t[2]-1
        ls1=t[0]
        ls2=t[1]
print(''.join(reversed(ans)))

实际上空间复杂度还能充分利用，这里核心是比较当前行和上一行，因此只需要一个数组就可以解决。数组占用空间min(m,n)。

s1=input()
s2=input()
ans=[]
ls1=len(s1)+1
ls2=len(s2)+1
A=[0]*ls2
tag=[]#用来标记斜箭头，例如5,6:4:'A'表示第5行 6列有公共字符‘A’LCS长度为4
for i in range(1,ls1):
    last=0;A[0]=0
    for j in range(1,ls2):
        up=A[j]
        if s1[i-1]!=s2[j-1]:
            A[j]=max(up,A[j-1])
        else:
            A[j]=last+1
            tag.append((i,j,A[j],s2[j-1]))
        last=up
ans=[]
goal=A[-1] #最长子序列值
for t in reversed(tag):
    if t[0]and t[1]and t[2]==goal:
        ans.append(t[3])
        goal=t[2]-1
        ls1=t[0]
        ls2=t[1]
print(''.join(reversed(ans)))

时间复杂度O( n2 )有点大？还可以进一步优化，将LCS问题转化为LIS（最长增序列）问题，用O( nlogn )来解决。参考1.

转化过程如下：
假设有两个序列 s1[ 1~6 ] = { a, b, c , a, d, c }, s2[ 1~7 ] = { c, a, b, e, d, a, b }。

1. 记录s1中每个元素在s2中出现的位置, 再将位置按降序排列, 则上面的例子可表示为：
   loc( a）= { 6, 2 }, loc( b ) = { 7, 3 }, loc( c ) = { 1 }, loc( d ) = { 5 }。
2. 将s1中每个元素的位置按s1中元素的顺序排列成一个序列s3 = { 6, 2, 7, 3, 1, 6, 2, 5, 1 }。
3. 在对s3求LIS得到的值即为求LCS的答案。

而LIS问题可以参考下一节。