并查集深度应用

先来看一道题目：岛屿

现在给你一个m*n矩阵，1表示陆地，0表示海，现在要你统计出这个矩阵上有几个小岛，上下左右联通的元素属于一座岛。

1 1 0 0 1 

1 0 1 1 1 

0 1 0 0 0 

上例就应该是3。

这题：很明显是在一个图上求联通分量，但是比联通分量还简单。

思路：

A.BFS

1.从点(1,1)开始，进行BFS，将遍历到的点都标记为2，结束一轮BFS，岛屿数量+1

2.遍历下一个节点，如果已经被标记为2，则直接跳过

复杂度分析：就是遍历所有为1的节点的复杂度，虽然遍历矩阵有两层循环，但是实际上的BFS只遍历了为1的点而已，O(n*m)。

#include
#include 
using namespace std;
int Map[105][105],total,m,n;

typedef struct{
    int x,y;
}Point;

void BFS(int x,int y){
    queueque;
    Point temp;
    int xx,yy;
    que.push(Point{x,y});
    while(!que.empty()){
        temp=que.front();
        que.pop();
        xx=temp.x;
        yy=temp.y;
        Map[xx][yy]=2;
        if(xx>1&&(Map[xx-1][yy]&1)){
            que.push(Point{xx-1,yy});
        }
        if(xx             que.push(Point{xx+1,yy});
        }
        if(yy>1&&(Map[xx][yy-1]&1)){
            que.push(Point{xx,yy-1});
        }
        if(yy             que.push(Point{xx,yy+1});
        }
    }
}

int main(){

    scanf("%d%d",&m,&n);
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            scanf("%d",&Map[i][j]);
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            if(Map[i][j]&1){
                BFS(i,j);
                total++;
            } 
        }
    } 
    printf("岛屿数量:%d",total);
    return 0;
} 
 

B.DFS  这是左神的思路：

实现一个infect(i,j)函数，这个函数会将(i,j)周围的点感染为2，同时，被感染的点递归地去感染他们周围的点。

#include
using namespace std;
int Map[105][105],total,m,n;
void infect(int x,int y){
    if(x<=0||x>m||y<=0||y>n||(Map[x][y]!=1)){
        return;
    }
    Map[x][y]=2;
    infect(x-1,y);
    infect(x+1,y);
    infect(x,y-1);
    infect(x,y+1);
}

int main(){
    scanf("%d%d",&m,&n);
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            scanf("%d",&Map[i][j]);
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            if(Map[i][j]&1){
                infect(i,j);
                total++;
            } 
        }
    } 
    printf("岛屿数量:%d",total);
    return 0;
}

左神思路分析：其实与BFS差不了多少，遍历的点的个数也基本相同，相对于BFS来说代码精简，缺陷就是：压栈和还原环境代价

 

改：如果现在这个矩阵十分大，使得你只能并行计算，求解。

并行计算的困难：当各个分块求出来之后，可能存在那种小块中分离，大块中合并的联通块。 

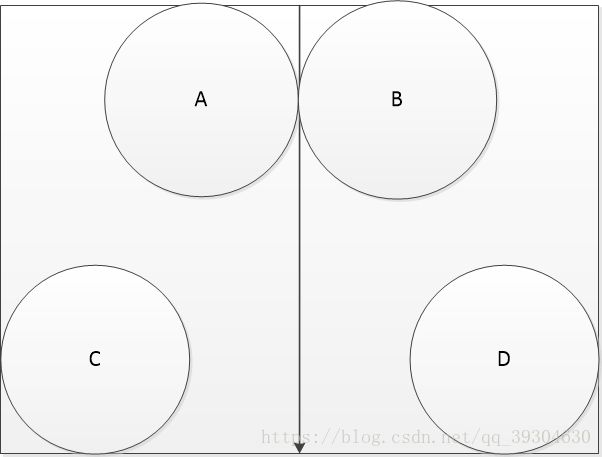
如图：A和B可能是属于同一个联通块的，但是并行计算中，由于划分，左边块和右边块各自有两个联通块，所以给小块合并带来了困难。

分析：对于处在边界的联通块要做特殊处理，所以我们需要这两块的分界线的边界信息。

以上图为例说明，左块有两个，右块有两个，当左右合并时，A、B是联通的，所以可以把他们合并，由于合并一次，就会减少一个联通块，所以是三个。

以矩阵为例做分析：

1 1 1 1 1 1 1 1 1 1 

0 1 1 1 1 1 1 0 0 0 

0 0 0 0 0 0 1 0 0 0 

0 0 1 0 0 1 1 0 1 1 

我们将这个矩阵分两半，

   左部                右部

1 1 1 1 1         1 1 1 1 1

0 1 1 1 1         1 1 0 0 0

0 0 0 0 0         0 1 0 0 0

0 0 1 0 0         1 1 0 1 1

我们将各个联通块标记出来：

   左部                右部

1 1 1 1 1         3 3 3 3 3

0 1 1 1 1         3 3 0 0 0

0 0 0 0 0         0 3 0 0 0

0 0 2 2 2        3 3 0 4 4

所以分开求有4个，我们将两条边界线单独拿出来：

左边     右边

   1           3

   1           3

   0           0

   2           3

第一行，1和3挨着且不属于一个集合，所以1和3集合合并，总数量-1变为3

第二行，1和3已经属于一个集合，往下

第三行，0和0，不连通，往下

第四行：2和3挨着且不属于一个集合，所以2和3集合合并，总数量-1变为2

结束

所以总的数量为2