python回归分析学习笔记2

import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

# statsmodels.OLS 的输入有 (endog, exog, missing, hasconst) 四个，我们现在只考虑前两个。
# 第一个输入 endog 是回归中的反应变量（也称因变量），是上面模型中的 y(t), 输入是一个长度为 k 的 array。
# 第二个输入 exog 则是回归变量（也称自变量）的值，即模型中的x1(t),…,xn(t)。
# 但是要注意，statsmodels.OLS 不会假设回归模型有常数项，没有专门的数值全为1的一列，Statmodels 有直接解决这个问题的函数：sm.add_constant()。
# 它会在一个 array 左侧加上一列 1。在 OLS 的模型之上调用拟合函数 fit()，才进行回归运算，
# 并且得到 statsmodels.regression.linear_model.RegressionResultsWrapper，它包含了这组数据进行回归拟合的结果摘要。
# 调用 params 可以查看计算出的回归系数 b0,b1,…,bn。

# 我们从最简单的一元模型开始，虚构一组数据。首先设定数据量k=100
samplesize=100
x=np.linspace(0, 10, samplesize)
# 使用 sm.add_constant() 在 array 上加入一列常项1。# 对1进行回归得到常数项b0
X = sm.add_constant(x)
# 然后设置模型里的 β0,β1，这里设置成 1,10。
beta = np.array([1, 10])
# 然后还要在数据中加上误差项，所以生成一个长度为k的正态分布样本。
e = np.random.normal(size=samplesize)
# 由此，我们生成反应项 y(t)。
y = np.dot(X, beta) + e

# 在反应变量和回归变量上使用 OLS() 函数
model = sm.OLS(y,X)
# 然后获取拟合结果。
results = model.fit()
# 再调取计算出的回归系数。
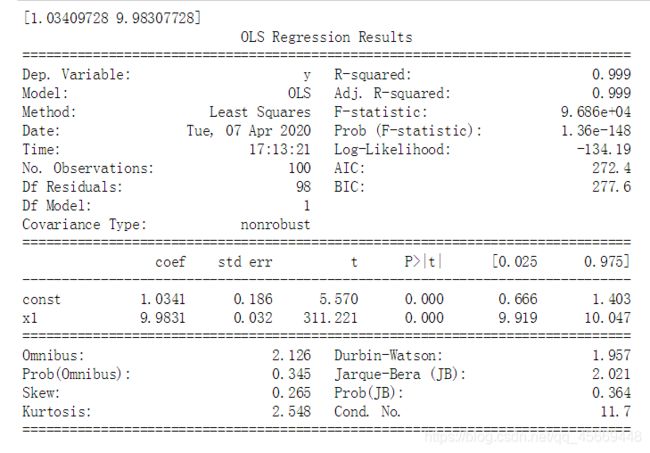
print(results.params)  #和实际的回归系数非常接近。
# 也可以将回归拟合的摘要全部打印出来。
print(results.summary())

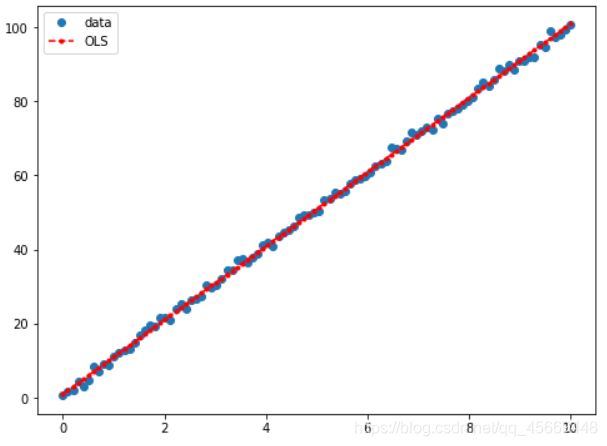
# 我们还可以将拟合结果画出来。先调用拟合结果的 fittedvalues 得到拟合的 y 值。
y_fitted = results.fittedvalues
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label='data')#画出原数据
ax.plot(x, y_fitted, 'r--.',label='OLS')#画出拟合数据
ax.legend(loc='best')

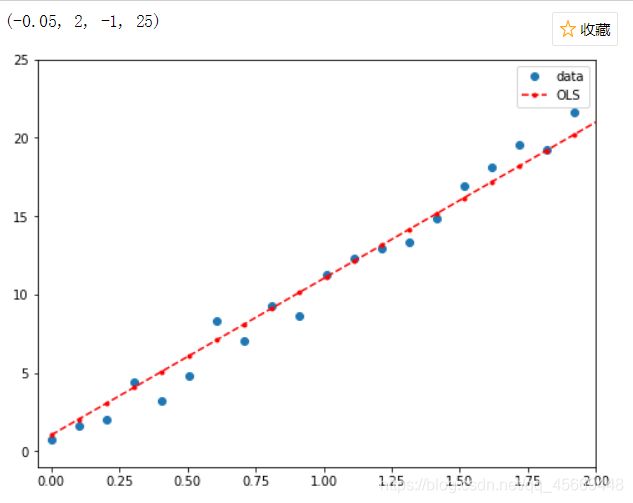
# 在大图中看不清细节，我们在 0 到 2 的区间放大一下，可以见数据和拟合的关系。
# 加入改变坐标轴区间的指令
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label='data')#画出原数据
ax.plot(x, y_fitted, 'r--.',label='OLS')#画出拟合数据
ax.legend(loc='best')
ax.axis((-0.05, 2, -1, 25)) # x轴：（-0.05, 2），y轴：（-1, 25）

# 高次模型的回归 以y=1+0.1X+10X^2为例
samplesize=100
x = np.linspace(0, 10, samplesize)
# 创建一个 k×2 的 array，两列分别为 x1 和 x2。我们需要 x2 为 x1 的平方。
X = np.column_stack((x, x**2)) 
# 使用 sm.add_constant() 在 array 上加入一列常项 1。
X = sm.add_constant(X)
# 然后设置模型里的 β0,β1,β2，我们设置成 1,0.1,10。
beta = np.array([1, 0.1, 10])
# 在数据中加上误差项
e = np.random.normal(size=samplesize)
# 由此，我们生成反应项 y(t)
y = np.dot(X, beta) + e
# 在反应变量和回归变量上使用 OLS() 函数。
model = sm.OLS(y,X)
# 然后获取拟合结果。
results = model.fit()
# 再调取计算出的回归系数。
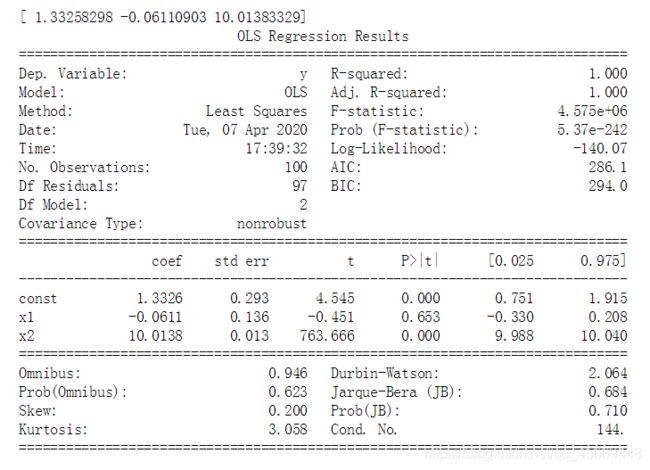
print(results.params)
# 获取全部摘要
print(results.summary())

# 哑变量
# 一般而言，有连续取值的变量叫做连续变量，它们的取值可以是任何的实数，
# 或者是某一区间里的任何实数，比如股价、时间、身高。
# 但有些性质不是连续的，只有有限个取值的可能性，一般是用于分辨类别，
# 比如性别、婚姻情况、股票所属行业，表达这些变量叫做分类变量。
# 在回归分析中，我们需要将分类变量转化为哑变量(dummy variable)。
# 如果我们想表达一个有 d 种取值的分类变量，那么它所对应的哑变量的取值
# 是一个 d 元组（可以看成一个长度为 d 的向量），其中有一个元素为 1，其他都是 0。
# 元素呈现出 1 的位置就是变量所取的类别。比如说，某个分类变量的取值是 {a,b,c,d}，
# 那么类别 a 对应的哑变量是(1,0,0,0)，b 对应 (0,1,0,0)，c 对应 (0,0,1,0)，d 对应 (0,0,0,1)。

# Statsmodels 里有一个函数 categorical() 可以直接把类别 {0,1,…,d-1} 转换成所对应的元组。
# 确切地说，sm.categorical() 的输入有 (data, col, dictnames, drop) 四个。
# 其中，data 是一个 k×1 或 k×2 的 array，其中记录每一个样本的分类变量取值。
# drop 是一个 Bool值，意义为是否在输出中丢掉样本变量的值。中间两个输入可以不用在意。
# 这个函数的输出是一个k×d 的 array（如果 drop=False，则是k×(d+1)），其中每一行是所对应的样本的哑变量；
# 这里 d 是 data 中分类变量的类别总数。
# 我们来举一个例子。这里假设一个反应变量 Y 对应连续自变量 X 和一个分类变量 Z。
# 常项系数为 10，X 的系数为 1；Z 有 {a,b,c}三个种类，其中 a 类有系数 1，b 类有系数 3，c 类有系数 8。
# 也就是说，将 Z 转换为哑变量 (Z1,Z2,Z3)，其中 Zi 取值于 0,1，有线性公式
# Y=10+X+Z1+3Z2+8Z3

# 我们按照这个关系生成一组数据来做一次演示。先定义样本数量为 50。
nsample = 50
# 设定分类变量的 array。前 20 个样本分类为 a。
groups = np.zeros(nsample, int)
# 之后的 20 个样本分类为 b。
groups[20:40] = 1
# 最后 10 个是 c 类。
groups[40:] = 2
# 转变成哑变量。
dummy = sm.categorical(groups, drop=True)

# 创建一组连续变量，是 50 个从 0 到 20 递增的值。
x = np.linspace(0, 20, nsample)
# 将连续变量和哑变量的 array 合并，并加上一列常项。
X = np.column_stack((x, dummy))
X = sm.add_constant(X)
# 定义回归系数。我们想设定常项系数为 10，唯一的连续变量的系数为 1，并且分类变量的三种分类 a、b、c 的系数分别为 1,3,8。
beta = [10, 1, 1, 3, 8]
# 再生成一个正态分布的噪音样本。
e = np.random.normal(size=nsample)
# 最后，生成反映变量。
y = np.dot(X, beta) + e
# 得到了虚构数据后，放入 OLS 模型并进行拟合运算。
result = sm.OLS(y,X).fit()
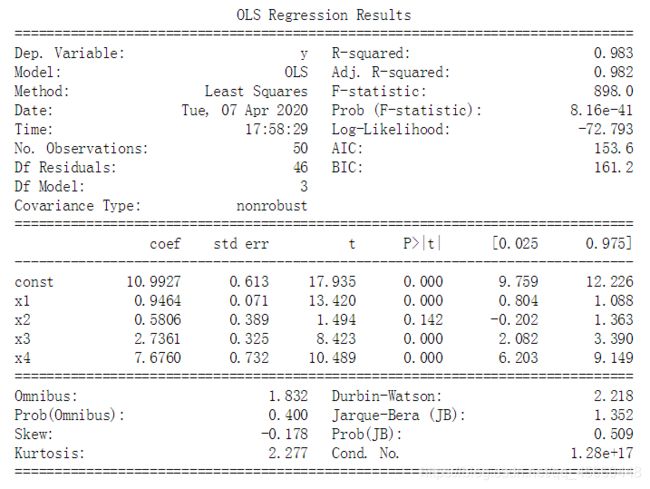
print(result.summary())

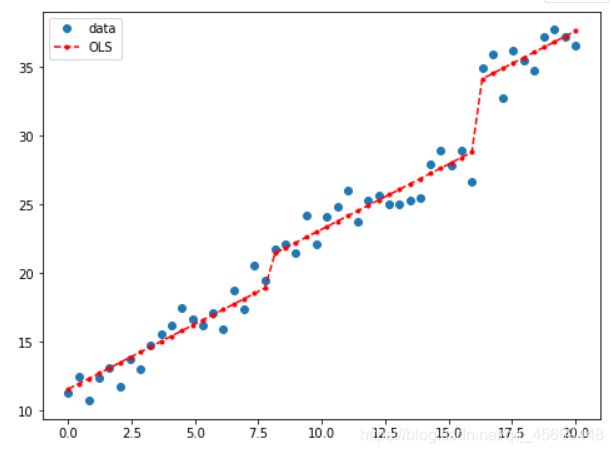
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, result.fittedvalues, 'r--.', label="OLS")
ax.legend(loc='best')