实验三:二叉树的基本操作,包括7种遍历方法(先序递归,中序递归,后序递归,先序非递归,中序非递归,后续非递归,层次遍历)判断结点的数目,比较结点的大小以及实验截图和程序框图
一、实验目的
1、掌握用指针类型描述、访问和处理二叉树的运算;
2、掌握二叉树的结构特征,以及各种存储结构的特点及适用范围;
3、熟练掌握递归程序设计方法、以及栈的应用
二、实验内容
以二叉链表作存储结构,编写程序,实现如下的功能:
1、根据输入的数据建立一个二叉树;
2、分别采用前序、中序、后序的遍历方式显示输出二叉树的遍历结果
3、采用非递归的编程方法,分别统计二叉树的节点个数、度为1、度为2和叶子节点的个数,以及数据值的最大值和最小值。
4、(选作内容)试编写按层次顺序遍历二叉树的算法。参考算法思想:要采用一个队列q,先将二叉树根结点入队列,然后退队列,输出该结点;若它有左子树,便将左子树根结点入队列;若它有右子树,便将右子树根结点入队列,直到队列空为止。因为队列的特点是先进先出,从而达到按层次顺序遍历二叉树的目的。
三、 实验要求
1.认真阅读和掌握本实验的算法。
2.上机将本算法实现。
3.在程序的编写中尽量与专业的编程规范靠拢,系统代码采用结构化的编程方式,力求设计代码以及注释等规范,
4.保存和打印出程序的运行结果,并结合程序进行分析。
实验报告正文:
1.需求分析
以无歧义的陈述说明程序设计的任务,强调的是程序要做什么?并明确规定:
输入的形式和输入值的范围;
(输出的形式;
(程序所能达到的功能;
(测试数据:包括正确的输入及其输出结果和含有错误的输入及其输出结果。
程序要做的就是通过先序遍历将二叉树创建,然后三种递归遍历,三种非递归遍历,层次遍历,找结点总数,叶子结点总数,度为1的结点总数,找最大的叶子节点的数值
(1).输入的形式:先序创建,空结点则为#不是空结点则输入数值
(2).程序所能达到的功能:先序遍历构建二叉树,然后7种遍历用来遍历二叉树,然后还有找最大结点,度为1的结点,叶子节点等等操作
(3).测试数据:
如下为AB#D##CE##F##的一颗二叉树
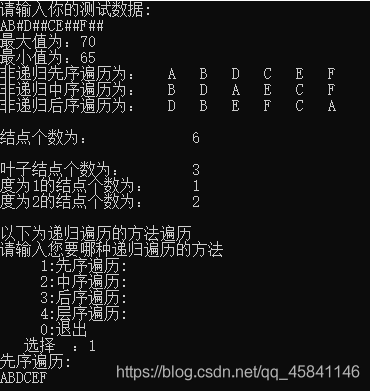
可以通过我们自己计算一下是符合的
以下是A#BC###这颗二叉树的几个基本操作
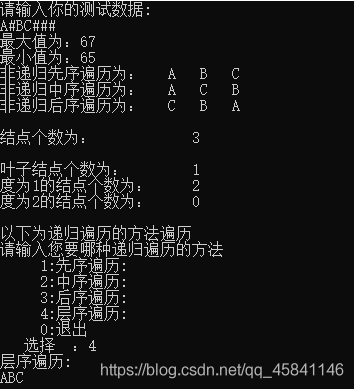
若直接为#,返回错误

2.概要设计
说明本程序中用到的所有抽象数据类型的定义、主程序的流程以及各程序模块之间的层次(调用)关系。
抽象数据类型是二叉树,在我的程序中就是TBinTree,node(二叉树),Queue, LinkQueue(队列)
主程序为先构建二叉树,然后进行三次非递归遍历,然后是找结点个数,最大最小结点数值,然后就是选择一种遍历方法:递归的先序遍历,递归的中序遍历,递归的后序遍历,以及层次遍历
调用关系就是主程序从上到下依次调用所用到的函数
3.详细设计
实现概要设计中定义的所有数据类型,对每个操作只需要写出伪码算法;对主程序和其他模块也都需要写出伪码算法(伪码算法达到的详细程度建议为:按照伪码算法可以在计算机键盘直接输入高级程序设计语言程序);画出函数和过程的调用关系图。
主函数:
伪代码
Main{
createTree//构建二叉树
PreOrderWithoutRecursion(T);//非递归先序遍历
InOrderWithoutRecursion(T);//非递归中序遍历
PostOrderWithoutRecursion(T);//非递归后续遍历
FindCount_0;
findCount_1;
findCount_2;
PreOrderTraverse(T);
InOrderTraverse(T);
PostOrderTraverse(T);
LevelOrderTraverse(T); //层次遍历
}
PreOrderTraverse(T){
visit(T);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
InOrderTraverse(T){
InOrderTraverse(T->lchild);
Visit(T);
InOrderTraverse(T->rchild);
}
PostOrderTraverse(T){
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
visit(T);
}
LevelOrderTraverse(T){
if(!T) return;
LinkQueue *Q = new LinkQueue;
InitQueue(Q,T);
while(Q->front->P) {
cout<<Q->front->P->data;
EnQueue(Q,Q->front->P->lchild);
EnQueue(Q,Q->front->P->rchild);
DeQueue(Q);
}
}
程序框图:

4.调试分析
内容包括:
调试过程中遇到的问题是如何解决的以及对设计与实现的回顾讨论和分析;
算法的时空分析(包括基本操作和其他算法的时间复杂度和空间复杂度的分析)和改进设想;经验和体会等。
调试过程会遇到很多问题,比如遇到了递归时关于返回值具体是多少的问题,以及在非递归中如何用栈结构,我都需要花一血时间去完成
本实验中的递归算法的时间复杂度要高一些,所以我认为用非递归算法来遍历二叉树要更能节省空间和时间
5.用户使用说明
说明如何使用你编写的程序,详细列出每一步的操作步骤。
使用的用户可以打开devC++等软件(C++的编译器)来进行编译和运行,按要求输入正确的输入格式,即先序遍历的方法输入,如果是空结点就输入‘#’,如果有数值就输入数值
6.测试结果
列出你的测试结果,包括输入和输出。这里的测试数据应该完整和严格,最好多于需求分析中所列。
(1).当树为完全二叉树时
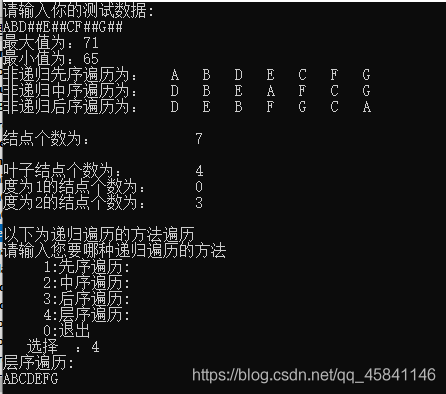
(2).当树不是完全二叉树时:
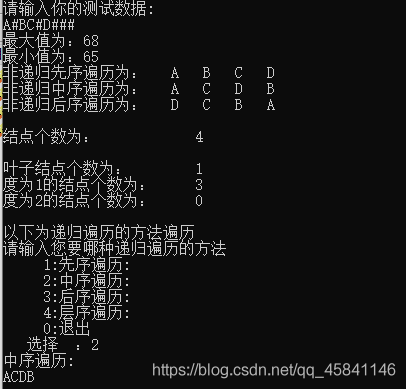
(3).当输入的数值为#时

直接返回error
7.附录
带注释的源程序代码。
值得注意的是,实习报告的各种文档资料,如:上述中的前三部分要在程序开发的过程中逐渐充实形成,而不是最后补写。
#include