推荐系统之阿里广告：Deep Interest Network for Click-Through Rate Predictioin

前言

　　阿里的商业广告CTR预测，使用了最新的Attention机制，我们来看一下是怎么用的，在相关的推荐工作中借鉴下经验。

为什么用Attention

为什么要用attention？
　　1） 业务中的发现，用户的历史行为数据，并不都对每一次的点击做贡献，而是仅仅有一部分在起作用。这就很像attention了，告知某些点上是与当前的状态最相关的。
　　举个栗子：一个爱好游泳的人，购买过泳衣，也购买过书籍，那么这次的广告里面，泳镜就更容易受到泳衣购买历史的影响。文中提到的“local activation”的用户特性。
　　2） 在应用其他的算法时，发现会将好多Embedding的特征，直接做累加等combinear等操作，简单粗暴有效，却会丢失好多信息。如果能在这里做些工作，会有更好的效果。
　　思考：在广告里面是这样的，那么在图文中是不是也有这样的特性。人的基本行为特点是不变的，也具有这样的特性仅部分历史行为对当前的点击是贡献最大的，而其他的可能就没啥贡献或者较少。实时反馈，是实时的attention，只不过偏近视，目光不长远。

怎么用

　　上个图，比较下一般的模型与DIN模型的差别，就知道在哪里具体使用Attention了。

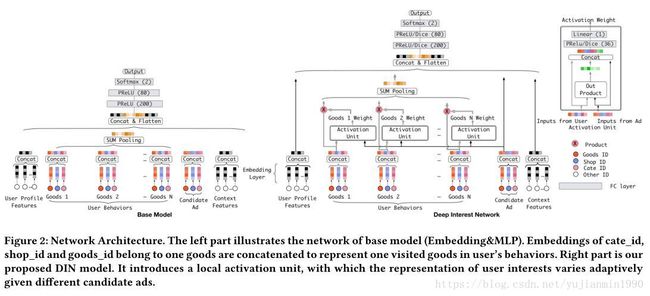
　　attention在这里的 实际意义是：每个Ad，都有一堆历史行为对其产生attention的影响分，这些attention分值与历史行为共同对这个Ad下的用户表示做加权。（可以将行为结构信息保留下来，并且提供了注意焦点）将上图中改进的地方展开，如下：
　　用户在某个广告下的Embedding表示 Vu(Va) V u ( V a ) ：

Vu(Va)=∑iNwi∗Va=∑iNg(Vi,Va)∗Va V u ( V a ) = ∑ i N w i ∗ V a = ∑ i N g ( V i , V a ) ∗ V a

　　小节点activation unit g g ：

g(Vi,Va)=PReLU([Vi,Va,Vi⊗Va])∗W g ( V i , V a ) = P R e L U ( [ V i , V a , V i ⊗ V a ] ) ∗ W

　　其中， Vi V i 是某个历史行为， Va V a 是广告的Embedding表示。

其他亮点

Evaluate Metric

GAUC: generation of AUC
　　单纯地用AUC评估，会带有用户偏差，若是将用户信息考虑进来则会更稳定更可信。

GAUC=∑ni=1wi∗AUCi∑ni=1wi G A U C = ∑ i = 1 n w i ∗ A U C i ∑ i = 1 n w i

　　 w w 可以是clicks或者impressions。这中AUC也应该是在个性化推荐里面更适合的，用户每个个体都有自己的AUC，这样才对嘛。

Dice Activation

　　一般的激活函数已经不能满足需求了，比如PReLU，这帮子人造了个强依赖数据的激活函数，根据数据动态地调整rectified-function。

　　其中PReLU是： f(s)={sass>0s≤0 f ( s ) = { s s > 0 a s s ≤ 0
　　新定义Dice: f(s)=p(s)s+(1−p(s))as f ( s ) = p ( s ) s + ( 1 − p ( s ) ) a s ，其中 p(s)=11+e−s−E[s]Var[s]+ϵ√ p ( s ) = 1 1 + e − s − E [ s ] V a r [ s ] + ϵ
　　当 s s 越大时， p(s) p ( s ) 越接近于1，这个时候 f(s) f ( s ) 越接近 s s ；当 s s 越小时， p(s) p ( s ) 越接近于0，这个时候 f(s) f ( s ) 越接近 as a s ，等于个 soft-rectified function，见上图。将数据做标准化估计，统一所有维度的量纲，也是个非常重要的技巧，有点类似BatchNormalized，但是这个地方时用来决定激活更偏向于哪侧的。在训练过程中，分别是当次batch的均值和方差。
　　在Test时，这里的 E[s]和Var[s] E [ s ] 和 V a r [ s ] 怎么估计呢？文中写到，则是moving_average，那么也就是 E[s]=γE[s]+(1−γ)1B∑Bisi E [ s ] = γ E [ s ] + ( 1 − γ ) 1 B ∑ i B s i ，同理 Var[s] V a r [ s ] 。

Regularization

　　稀疏输入，为什么会overfitting呢？这个跟数据分布有关系，互联网时代的数据特点，超长尾头部重，头重（小比例的特征频繁出现）容易过拟合，长尾（大比例的特征低频出现）则容易带来噪声，不好学。当增加细粒度的特征时，也极其容易由于细粒度的样本过于密集而带来负面效果。怎么办呢？在这里根据样本在当前batch内出现的频次做了正则约束。 L L 是二分交叉熵。

wj=wj−η[1B∑(xi,yi)∈Batch∂L(f(xi),yi)∂wj+λwjnjIj] w j = w j − η [ 1 B ∑ ( x i , y i ) ∈ B a t c h ∂ L ( f ( x i ) , y i ) ∂ w j + λ w j n j I j ]

　　其中 Ij={10∃(xi,yi)∈Batch,s.t.[xi]j≠0otherwises I j = { 1 ∃ ( x i , y i ) ∈ B a t c h , s . t . [ x i ] j ≠ 0 0 o t h e r w i s e s ， nj n j 表示当次batch中第 j j 个特征出现的频次。
　　频次出现越高的特征，则被惩罚地弱， w w 越容易扩散；频次出现的越少的特征，则被惩罚地强， w w 越收敛在较小范围内。（理论上是应该用全部样本统计的 nj n j ，但是这里仅在batch内统计 nj n j 就做为估计值使用了，不碍事。多想一下，如果真用全部的统计是不是会更好呢？）
　　其正则约束的完整形式如下（当前batch）：

L2(w)=∑j=1K∑i=1BIj(xi,j≠0)nj||wj||22 L 2 ( w ) = ∑ j = 1 K ∑ i = 1 B I j ( x i , j ≠ 0 ) n j | | w j | | 2 2

思考

1. 图文推荐也可以使用Attention来专门处理推荐时的part-contribution问题，补充实时反馈的缺陷。
2. 大规模的稀疏数据，需要特别小心处理长尾头重问题，这里使用的改进版正则和激活是值得借鉴的。
3. 离线评估的GAUC更稳定可信，再上线A/B。

Reference

1. 2017- Deep Interest Network for Click-Through Rate Prediction paper
2. 2018- Deep Interest Network for Click-Through Rate Prediction paper