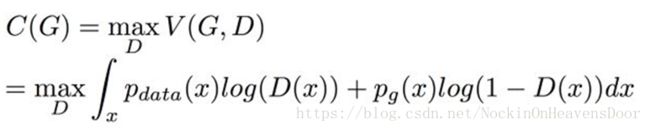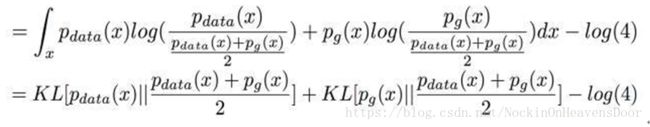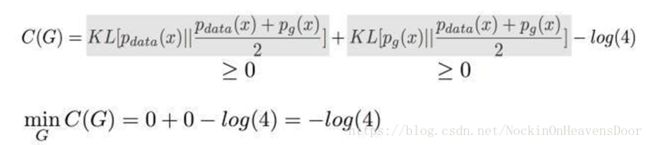GANs：原始生成对抗网络论文分析及tensorflow、pytorch代码解析

先给出记录的原论文笔记。

- 生成式对抗网络 GAN (Generative adversarial networks)：由一个生成器(generator)和一个判别器(discriminator)构成. 生成器捕捉真实数据样本的潜在分布(latent distribution), 并生成伪造的数据样本; 判别器是一个二分类器, 判别输入是真实数据还是生成的样本. 生成器和判别器在作者原文中使用得是多层感知机(multilayer perceptron).

- 训练的过程：判别器的目的是区分一个样本是来自模型分布(生成器产生)还是数据真实分布；生成器的目的是尽量模拟得到真实数据的分布，从而产生的数据可以让判别器误判为真实数据。原文已经说明这个模型的训练用后向传播完成，不需要用到马尔科夫链和近似推理。

符号定义：

目标函数：

原文中用k步优化D之后一步优化G，其中k设置为1.

• 训练过程如图：
  

这里，z是噪声数据，从z中采样作为x，形成绿色的高耸的部分，原始数据Xdata是不变的。

蓝色虚线是分类器(sigmoid),黑色虚线是原始数据，绿色实线是生成数据。

最初的时候D可以很好的区分开真实数据和生成数据，看图(b)，对于蓝色虚线而言，单纯的绿色部分可以很明确的划分为0，黑色虚线的部分可以很明确的划分成1，二者相交的部分划分不是很明确。

这张图形象的说明了一下G和D的优化方向。优化D的时候需要很好的画出黑色虚线，使它能够区分开真实数据和生成数据。优化G的时候，生成数据更加接近原始数据的样子，使得D难以区分数据真假。如此反复直到最后再也画不出区分的黑色虚线。

优化算法：

注：这里的动量(momentum)梯度下降是较为平凡的一种梯度优化方法。

红线处是积分换元。

1、证明D*G(x)是最优解

由于V是连续的所以可以写成积分的形式来表示期望：

通过假设x=G(z)可逆进行了变量替换，整理式子后得到：

然后对V(G,D)进行最大化：对D进行优化令V取最大：

取极值，对V进行求导并令导数等于0.求解出来可得D的最佳解D*G(x)结果一样。

2、假设我们已经知道D*G(x)是最佳解了，这种情况下G想要得到最佳解的情况是：G产生出来的分布要和真实分布一致，即：

在这个条件下，D*G(x)=1/2。

接下来看G的最优解是什么，因为D的这时已经找到最优解了，所以只需要调整G ，令

对于D的最优解我们已经知道了，D*G(x)，可以直接把它带进来 并去掉前面的Max

然后对 log里面的式子分子分母都同除以2，分母不动，两个分子在log里面除以2 相当于在log外面 -log(4) 可以直接提出来：

结果可以整理成两个KL散度-log(4)

KL散度是大于等于零的，所以C的最小值是 -log（4），当且仅当

所以证明了 当G产生的数据和真实数据是一样的时候，C取得最小值也就是最佳解。

关于Jensen-Shannon divergence:

Tensorflow 代码：

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import os

Xavier初始化网络参数：

def xavier_init(size):
    in_dim = size[0]
    xavier_stddev = 1. / tf.sqrt(in_dim / 2.)
    return tf.random_normal(shape=size, stddev=xavier_stddev)

GAN需要两个网络作为判别器和生成器，可以用复杂的网络如卷积网络或者多层感知机(原论文)。这里用两层神经网络：

# Discriminator Net
X = tf.placeholder(tf.float32, shape=[None, 784])

D_W1 = tf.Variable(xavier_init([784, 128]))
D_b1 = tf.Variable(tf.zeros(shape=[128]))

D_W2 = tf.Variable(xavier_init([128, 1]))
D_b2 = tf.Variable(tf.zeros(shape=[1]))

theta_D = [D_W1, D_W2, D_b1, D_b2]

# Generator Net
Z = tf.placeholder(tf.float32, shape=[None, 100])

G_W1 = tf.Variable(xavier_init([100, 128]))
G_b1 = tf.Variable(tf.zeros(shape=[128]))

G_W2 = tf.Variable(xavier_init([128, 784]))
G_b2 = tf.Variable(tf.zeros(shape=[784]))

theta_G = [G_W1, G_W2, G_b1, G_b2]

定义从均匀分布采样的函数：

def sample_Z(m, n):
    return np.random.uniform(-1., 1., size=[m, n])

定义生成器和判别器：

def generator(z):
    G_h1 = tf.nn.relu(tf.matmul(z, G_W1) + G_b1)
    G_log_prob = tf.matmul(G_h1, G_W2) + G_b2
    G_prob = tf.nn.sigmoid(G_log_prob)

    return G_prob


def discriminator(x):
    D_h1 = tf.nn.relu(tf.matmul(x, D_W1) + D_b1)
    D_logit = tf.matmul(D_h1, D_W2) + D_b2
    D_prob = tf.nn.sigmoid(D_logit)

    return D_prob, D_logit

generator(z) 的输入是100维返回是786维，MNIST 图片大小(28x28).

Z是G(Z)的先验。

其中判别器返回第二个参数是输出x的logit，也就是output层的输出。

定义样本绘图函数：

def plot(samples):
    fig = plt.figure(figsize=(4, 4))
    gs = gridspec.GridSpec(4, 4)
    gs.update(wspace=0.05, hspace=0.05)

    for i, sample in enumerate(samples):
        ax = plt.subplot(gs[i])
        plt.axis('off')
        ax.set_xticklabels([])
        ax.set_yticklabels([])
        ax.set_aspect('equal')
        plt.imshow(sample.reshape(28, 28), cmap='Greys_r')

    return fig

实现论文中algorithm 1的损失函数：

G_sample = generator(Z)
D_real, D_logit_real = discriminator(X)
D_fake, D_logit_fake = discriminator(G_sample)

# D_loss = -tf.reduce_mean(tf.log(D_real) + tf.log(1. - D_fake))
# G_loss = -tf.reduce_mean(tf.log(D_fake))

要对D_loss最大化所以前面有负号，因为tensorflow的optimizer只能最小化。

论文同样建议，算法中最大化tf.reduce_mean(tf.log(D_fake)) 比最小化tf.reduce_mean(1 - tf.log(D_fake))要更好。

另一种损失形式：

# Alternative losses:
# -------------------
D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_real, labels=tf.ones_like(D_logit_real)))
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_fake, labels=tf.zeros_like(D_logit_fake)))
D_loss = D_loss_real + D_loss_fake
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_fake, labels=tf.ones_like(D_logit_fake)))

训练GANs：

D_solver = tf.train.AdamOptimizer().minimize(D_loss, var_list=theta_D)
G_solver = tf.train.AdamOptimizer().minimize(G_loss, var_list=theta_G)

mb_size = 128
Z_dim = 100

mnist = input_data.read_data_sets('../../MNIST_data', one_hot=True)

sess = tf.Session()
sess.run(tf.global_variables_initializer())

if not os.path.exists('out/'):
    os.makedirs('out/')

i = 0

for it in range(1000000):
    if it % 1000 == 0:
        samples = sess.run(G_sample, feed_dict={Z: sample_Z(16, Z_dim)})

        fig = plot(samples)
        plt.savefig('out/{}.png'.format(str(i).zfill(3)), bbox_inches='tight')
        i += 1
        plt.close(fig)

    X_mb, _ = mnist.train.next_batch(mb_size)

    _, D_loss_curr = sess.run([D_solver, D_loss], feed_dict={X: X_mb, Z: sample_Z(mb_size, Z_dim)})
    _, G_loss_curr = sess.run([G_solver, G_loss], feed_dict={Z: sample_Z(mb_size, Z_dim)})

    if it % 1000 == 0:
        print('Iter: {}'.format(it))
        print('D loss: {:.4}'. format(D_loss_curr))
        print('G_loss: {:.4}'.format(G_loss_curr))
        print()

pytorch代码:

---

结论：

为什么我们对训练GaN感兴趣？

可能是因为数据的概率分布Pdata很复杂，而且很难推断。所以，能从Pdata 生成样本而不必处理讨厌的概率分布的generative machine是非常好的。这样，我们就可以用它来处理另一个需要样本的过程，因为我们可以用训练好的Generative Net相对便宜地得到样本。

参考：
1.《Goodfellow, Ian, et al. “Generative adversarial nets.” Advances in Neural Information Processing Systems. 2014》
2. https://wiseodd.github.io/techblog/2016/09/17/gan-tensorflow/
3. https://zhuanlan.zhihu.com/p/28853704