Codeforces 1016E. Rest In The Shades （二分查找、简单几何）

• 原题链接：http://codeforces.com/contest/1016/problem/E
• 题意简述：

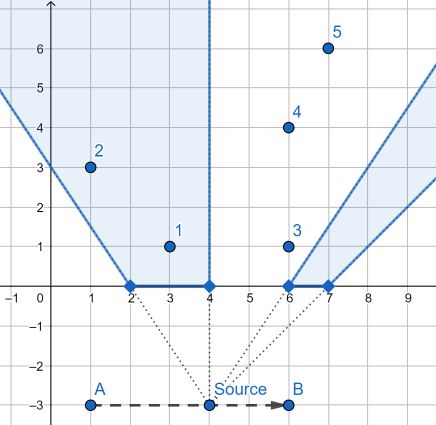
平面上有一个点光源，它以每秒1单位长度的速度从点  移动到点   。

 轴正方向上有 个 不相交不接触的栅栏，它们可以表示为  。当点  与点光源的连线与某个栅栏相交或接触时，称点在阴影内。

给定  个点，求出每个点在点光源从点  移动到点  时，处在阴影内的总时间  。

• 输入与数据范围：

行 

 行 

• 输出：

 行  ，绝对误差或相对误差不超过 

• 解题思路：

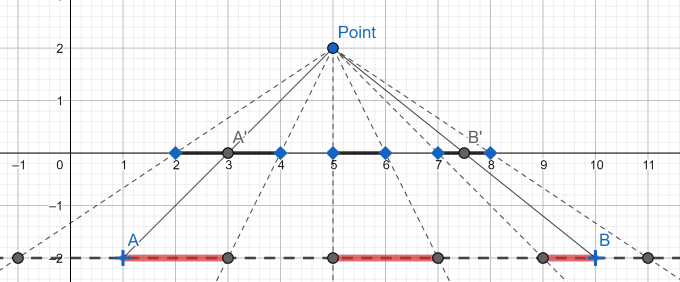
根据相似三角形原理，连接点 和 ，交  轴于两点  ，求出  中栅栏的占比，然后放大到  上就可以了。注意到题目中的栅栏的单调性和数目，二分求出  附近的线段，用前缀和求出总长度，然后求其是否相交，若相交则减去一部分长度即可。

复杂度：

• 代码：

#include 
using namespace std;

double sy, a, b;
#define eps 1e-8

double fencel[200005];
double fencer[200005];
double pre[200005];

int main() {

	scanf("%lf%lf%lf", &sy, &a, &b);

	int n;
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%lf%lf", &fencel[i], &fencer[i]);
		pre[i + 1] = pre[i] + (fencer[i] - fencel[i]);
	}

	int q;
	scanf("%d", &q);
	for (int i = 0; i < q; i++) {
		double x, y;
		scanf("%lf%lf", &x, &y);

		double sfb = (y - 0) / (y - sy);
		double pax = a - x;
		double pbx = b - x;

		pax = pax * sfb;
		pbx = pbx * sfb;

		pax = x + pax;
		pbx = x + pbx;

		if (pbx <= fencel[0]) {
			printf("0.000000000000000\n");
			continue;
		}

		if (pax >= fencer[n - 1]) {
			printf("0.000000000000000\n");
			continue;
		}

		int l = 0, r = n - 1, mid;
		while (l <= r) {
			mid = (l + r) / 2;
			if (fencer[mid] > pax + eps)	r = mid - 1;
			else l = mid + 1;
		}

		l = r + 1;
		double left = pre[l + 1];
		left -= min(fencer[l] - fencel[l], (fencer[l] - pax));

		l = 0, r = n - 1;
		while (l <= r) {
			mid = (l + r) / 2;
			if (fencel[mid] < pbx - eps)l = mid + 1;
			else r = mid - 1;
		}

		r = l - 1;
		double right = pre[n] - pre[r];
		right -= min(fencer[r] - fencel[r], pbx - fencel[r]);

		double time = (b - a)*(pre[n] - right - left) / (pbx - pax);
		printf("%.15f\n", time);
	}
	return 0;
}

• 其他：

1.使用 scanf 和 printf 来读写，若使用 cin 和 cout 会 TLE 。

2.二分的时候注意根据要求的不同情况处理不同边界，或者使用 lower_bound 定位到附近然后暴力循环找出所求线段。

3.求交点的方法：

      先把两条直线表示为向量，任取其中一个向量的一端求其到另一条直线的距离，然后根据比例将该向量放缩到直线上，所得的向量即为交点坐标。在本题中，直线取作  轴，距离当然就是纵坐标的差值了，同理放缩即可。