A*算法解决八数码问题(C++类改进版)
八数码问题:
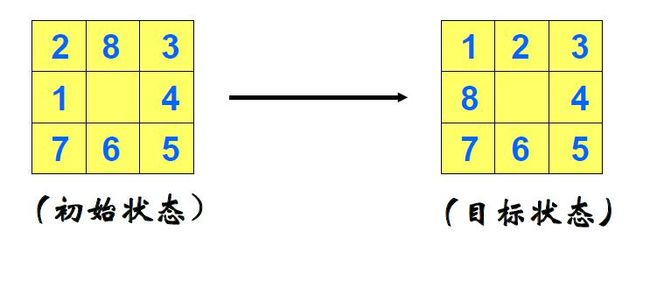
在一个3*3的棋盘中,分别用1,2,3,...,8表示八个数码方格,用0表示空缺的方格,现给出一个初始状态和目标状态,寻找出在评估函数f(n)=g(n)+h(n)的限制下,以最少的步数到达目标状态(一次将一个数码方格移动到空缺的方格中);其中,g(n)表示n节点与目标状态的“距离”,h(n)表示n节点与初始状态的距离。
现在令g(n)为当前节点n与目标状态数码方格位置不同的个数,h(n)为节点的深度。
定义node类:
class node{
public:
int number[row][col];//二维数组表示数码
string str;//数码移动方向("up","down","left","right")
int distances;//g(n)
int depth;//h(n)
int findex;//父节点的位置
node(){
}
int dis();//计算并返回distances
void voluation(int index);//赋值为v[index]
bool isend();//是否为目标状态
bool isequal(node q);//当前节点和节点q是否相等
};定义全局:
vector v;//使用vector储存节点
node father,intent;//定义初始状态和目标状态 类外定义函数:
void node::voluation(int index){
for(int i=0;i定义函数如下:
bool isexpansive(node &n){//判断n是否可以扩展,即判断v内是否有节点和n相等
for(int i=0;iint find_min(){//在v中寻找评估值最小的节点作为下一步的扩展节点
int min_x=maxnum;
int index_min;
for(int i=0;ivoid breath(int index){//扩展v[index]
int index_x,index_y;
int flag=0;
for(int i=0;i0){//空格向上,即空格上的数码往下移动一格,下同
swap_t(upnode.number[index_x][index_y],upnode.number[index_x-1][index_y]);
if(isexpansive(upnode)){
up_dis=upnode.dis();
upnode.findex=index;
upnode.depth=v[index].depth+1;
upnode.str="down";
v.push_back(upnode);
}
}
if(index_x<2){
swap_t(downnode.number[index_x][index_y],downnode.number[index_x+1][index_y]);
if(isexpansive(downnode)){
down_dis=downnode.dis();
downnode.findex=index;
downnode.depth=v[index].depth+1;
downnode.str="up";
v.push_back(downnode);
}
}
if(index_y>0){
swap_t(leftnode.number[index_x][index_y],leftnode.number[index_x][index_y-1]);
if(isexpansive(leftnode)){
left_dis=leftnode.dis();
leftnode.findex=index;
leftnode.depth=v[index].depth+1;
leftnode.str="right";
v.push_back(leftnode);
}
}
if(index_y<2){
swap_t(rightnode.number[index_x][index_y],rightnode.number[index_x][index_y+1]);
if(isexpansive(rightnode)){
right_dis=rightnode.dis();
rightnode.findex=index;
rightnode.depth=v[index].depth+1;
rightnode.str="left";
v.push_back(rightnode);
}
}
v[index].distances=maxnum;//v[idnex]已扩展完毕,设为不可“访问”点
} void print(int index, vector& rstep_v)//利用rstep_v输出从index到达目标节点的过程
{
rstep_v.push_back(v[index]);
index = v[index].findex;
while (index != 0)
{
rstep_v.push_back(v[index]);//把过程中所有的节点保存在rstep_v中
index = v[index].findex;
}
for (int i = rstep_v.size() - 1; i >= 0; i--){
cout << "Step " << rstep_v.size() - i<< endl;
node p=rstep_v[i];
cout< void process(){
while(1){
int t=0;//break标志
if(isempty()){//发生异常:还未到目标状态时v中节点都已扩展完毕
cout << "error" << endl;
exit(-1);
}
else{
int best=find_min();
node temp=v[best];//找出最优节点
if(temp.isend()){//最优结点为目标状态时,输出过程
t=1;//已到达目标状态,t为1
vector rstep_v;
print(best,rstep_v);
}
else{//未到达目标状态,扩展最优结点
breath(best);
}
}
if(t)//已到达目标状态,退出循环
break;
}
} 完整代码如下:
#include
#include
#include
#define col 3
#define row 3
#define maxnum 10000
#define maxdistance 10000
using namespace std;
class node{
public:
int number[row][col];
string str;
int distances;
int depth;
int findex;
node(){
}
int dis();
void voluation(int index);
bool isend();
bool isequal(node q);
};
vector v;
node father,intent;
void node::voluation(int index){
for(int i=0;i0){
swap_t(upnode.number[index_x][index_y],upnode.number[index_x-1][index_y]);
if(isexpansive(upnode)){
up_dis=upnode.dis();
upnode.findex=index;
upnode.depth=v[index].depth+1;
upnode.str="down";
v.push_back(upnode);
}
}
if(index_x<2){
swap_t(downnode.number[index_x][index_y],downnode.number[index_x+1][index_y]);
if(isexpansive(downnode)){
down_dis=downnode.dis();
downnode.findex=index;
downnode.depth=v[index].depth+1;
downnode.str="up";
v.push_back(downnode);
}
}
if(index_y>0){
swap_t(leftnode.number[index_x][index_y],leftnode.number[index_x][index_y-1]);
if(isexpansive(leftnode)){
left_dis=leftnode.dis();
leftnode.findex=index;
leftnode.depth=v[index].depth+1;
leftnode.str="right";
v.push_back(leftnode);
}
}
if(index_y<2){
swap_t(rightnode.number[index_x][index_y],rightnode.number[index_x][index_y+1]);
if(isexpansive(rightnode)){
right_dis=rightnode.dis();
rightnode.findex=index;
rightnode.depth=v[index].depth+1;
rightnode.str="left";
v.push_back(rightnode);
}
}
v[index].distances=maxnum;
}
ostream& operator<<(ostream& os, node& no)
{
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++)
os << no.number[i][j] << ' ';
os << endl;
}
return os;}
void print(int index, vector& rstep_v)
{
rstep_v.push_back(v[index]);
index = v[index].findex;
while (index != 0)
{
rstep_v.push_back(v[index]);
index = v[index].findex;
}
for (int i = rstep_v.size() - 1; i >= 0; i--){
cout << "Step " << rstep_v.size() - i<< endl;
node p=rstep_v[i];
cout< rstep_v;
print(best,rstep_v);
}
else{
breath(best);
}
}
if(t)
break;
}
}
int main()
{
cout << "Input source:" << endl;
for(int i=0;i>father.number[i][j];
}
}
father.findex=0;
father.depth=0;
cout << "Input end:" << endl;
for(int i=0;i>intent.number[i][j];
}
}
v.push_back(father);
process();
return 0;
} Input source:
1 2 3 4 5 6 7 8 0
Input end:
1 0 2 3 4 5 6 7 8
Step 1
down
1 2 3
4 5 0
7 8 6
Step 2
right
1 2 3
4 0 5
7 8 6
Step 3
right
1 2 3
0 4 5
7 8 6
Step 4
up
1 2 3
7 4 5
0 8 6
Step 5
left
1 2 3
7 4 5
8 0 6
Step 6
left
1 2 3
7 4 5
8 6 0
Step 7
down
1 2 3
7 4 0
8 6 5
Step 8
down
1 2 0
7 4 3
8 6 5
Step 9
right
1 0 2
7 4 3
8 6 5
Step 10
up
1 4 2
7 0 3
8 6 5
Step 11
up
1 4 2
7 6 3
8 0 5
Step 12
right
1 4 2
7 6 3
0 8 5
Step 13
down
1 4 2
0 6 3
7 8 5
Step 14
left
1 4 2
6 0 3
7 8 5
Step 15
left
1 4 2
6 3 0
7 8 5
Step 16
up
1 4 2
6 3 5
7 8 0
Step 17
right
1 4 2
6 3 5
7 0 8
Step 18
right
1 4 2
6 3 5
0 7 8
Step 19
down
1 4 2
0 3 5
6 7 8
Step 20
left
1 4 2
3 0 5
6 7 8
Step 21
down
1 0 2
3 4 5
6 7 8