【算法+OpenCV】基于三次Bezier原理的曲线拟合算法C++与OpenCV实现

近期，因为要实现经过多个控制点的曲线拟合，研究起了曲线拟合算法。综合搜索到的资料，发现Bezier曲线拟合算法是一种相对较容易实现、且拟合的效果较好的算法。关于Bezier曲线原理，请参照（Bezier曲线原理），这里就不再做具体介绍了，我们使用的是Besier三次曲线拟合原理。下面主要介绍算法的实现过程。

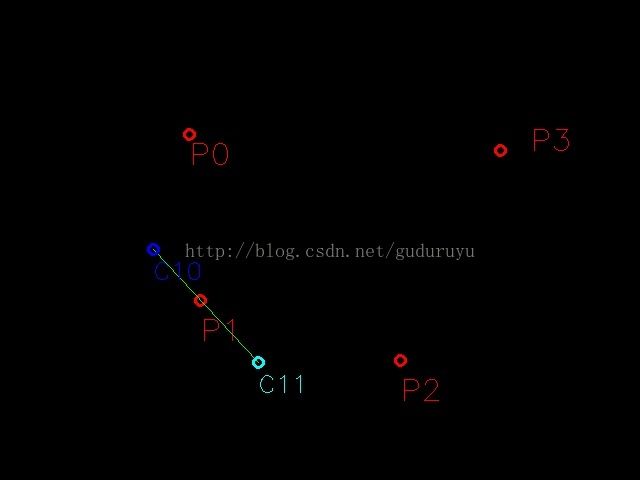
如下图中，P0、P1、P2、P3四个点，我们最终是想获取过这四个点的封闭平滑曲线。

根据Bezier三次曲线拟合的原理，我们可以分别拟合P0P1、P1P2、P2P3、P3P0四段曲线，进而连接成一个封闭的曲线。但是，Bezier三次曲线拟合需要在两点之间找到两个控制点。每个点的控制点可以根据其前后相邻的两点获得，具体实现如下：

void get_control_points(double x0, double y0, double x1, double y1, double x2, double y2,
	double& p1x, double& p1y, double& p2x, double& p2y, double t)
{
	double d01 = sqrt(pow(x1 - x0, 2) + pow(y1 - y0, 2));
	double d12 = sqrt(pow(x2 - x1, 2) + pow(y2 - y1, 2));

	double fa = t * d01 / (d01 + d12);
	double fb = t * d12 / (d01 + d12);

	p1x = x1 - fa * (x2 - x0);
	p1y = y1 - fa * (y2 - y0);
	p2x = x1 + fb * (x2 - x0);
	p2y = y1 + fb * (y2 - y0);

	return;
}

其中，（x0，y0）、（x1，y1）、（x2，y2）分别为P0、P1、P2三点的坐标；t为曲率因子（取值范围0-1.0），影响的是拟合曲线的曲率，后面将对其作进一步介绍。根据三点的坐标和t，即可求得P1点的两个控制点C10（p1x，p1y）、C11(p2x，p2y)。

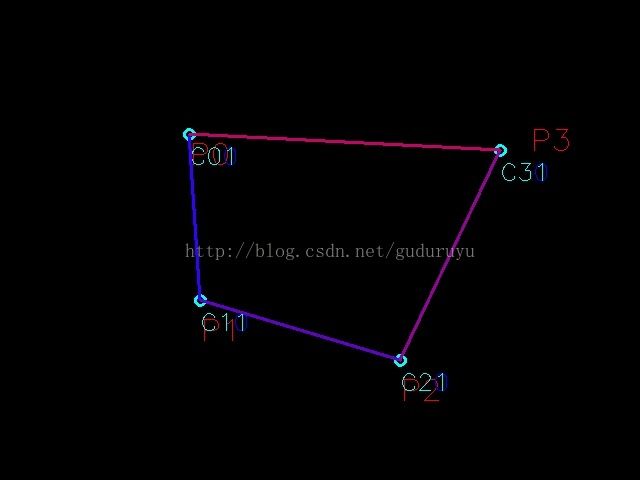
以此类推，我们可分别求得P2、P3、P0等各点的控制点，如下图所示。

接下来，我们我们逐段绘制Besier曲线。通过两个顶点P0、P1和两个控制点C01、C10，根据Bezier曲线拟合原理，即可获得连接P0、P1两点的曲线。

void get_bezier(double x1, double y1, double x2, double y2, double p12x, double p12y,
	double p21x, double p21y, std::vector& vec_x, std::vector & vec_y)
{
	int prev_x = (int)round(x1);
	int prev_y = (int)round(y1);
	int last_x = (int)round(x2);
	int last_y = (int)round(y2);

	for (double s = 0.0; s < (1.0 + 0.00001); s += DELTA_S)
	{
		double J0 = pow(1 - s, 3);
		double J1 = pow(1 - s, 2) * s * 3;
		double J2 = pow(s, 2) * (1 - s) * 3;
		double J3 = pow(s, 3);

		double ptx = x1 * J0 + p12x * J1 + p21x * J2 + x2 * J3;
		double pty = y1 * J0 + p12y * J1 + p21y * J2 + y2 * J3;

		int iptx = (int)round(ptx);
		int ipty = (int)round(pty);

		vec_x.push_back(iptx);
		vec_y.push_back(ipty);
	}
	return;
}

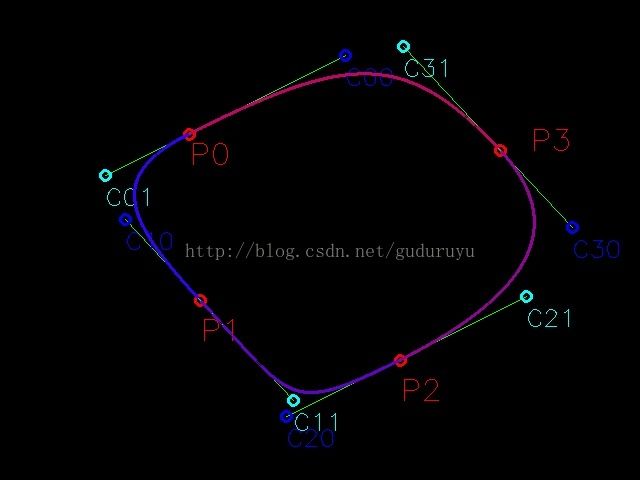
其中，DELTA_S是拟合的步长。再通过轮廓查找算法和插值算法，即可得到一段完整的Besier曲线，如下图所示。

同样，以此类推，我们可以分别得到P1P2、P2P3、P3P0之间的曲线，将这几段曲线连接在一起，即可得到一条完整的封闭曲线。

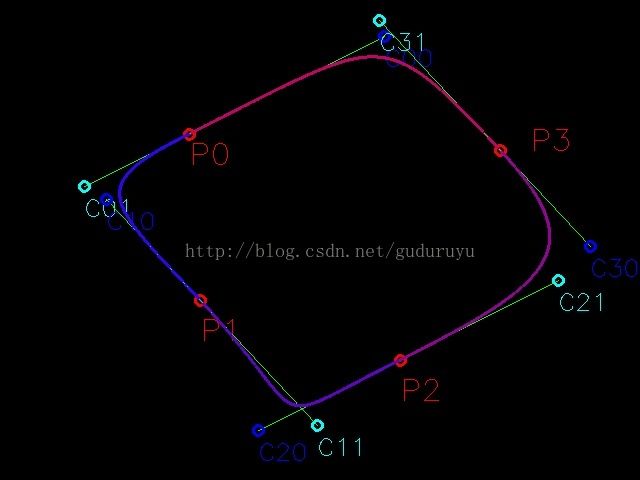
最后，我们再看一看前文提到的曲率因子t对拟合出来的曲线的影响。分别令 t = 0.0、0.2、0.5、0.8、1.0，得到的曲线分别如下图所示。

下面是基于OpenCV的完整实现代码：

#include "spline_curve.h"
#include 

#define DELTA_S			0.01
#define T				0.5


void get_control_point(cv::Point2d& point0, cv::Point2d& point1, cv::Point2d& point2,
	cv::Point2d& c01, cv::Point2d& c12, double t)
{
	double d01 = sqrt(pow(point1.x - point0.x, 2) + pow(point1.y - point0.y, 2));
	double d12 = sqrt(pow(point2.x - point1.x, 2) + pow(point2.y - point1.y, 2));


	double fa = t * d01 / (d01 + d12);
	double fb = t * d12 / (d01 + d12);

	c01.x = point1.x - fa * (point2.x - point0.x);
	c01.y = point1.y - fa * (point2.y - point0.y);
	c12.x = point1.x + fb * (point2.x - point0.x);
	c12.y = point1.y + fb * (point2.y - point0.y);

	return;
}

void get_control_points_array(std::vector& key_points, std::vector& vec_c01, 
	std::vector& vec_c02, double t)
{
	int N = key_points.size();

	for (int i = 0; i < N; i++)
	{
		cv::Point2d c01, c02;

		if (i == 0)
		{
			get_control_point(key_points[N - 1], key_points[i], key_points[i + 1], c01, c02, t);
			vec_c01.push_back(c01);
			vec_c02.push_back(c02);
		}
		else if (i < (N - 1))
		{
			get_control_point(key_points[i - 1], key_points[i], key_points[i + 1], c01, c02, t);
			vec_c01.push_back(c01);
			vec_c02.push_back(c02);
		}
		else
		{
			get_control_point(key_points[i - 1], key_points[i], key_points[0], c01, c02, t);
			vec_c01.push_back(c01);
			vec_c02.push_back(c02);
		}
	}
}


bool is_adjcent_point(cv::Point2i& point1, cv::Point2i& point2)
{
	if (((point1.x == point2.x) && (point1.y == point2.y)) || 
		(std::abs(point1.x - point2.x) > 1) || (std::abs(point1.y - point2.y) > 1))
	{
		return false;
	}

	return true;
}

bool is_same_point(cv::Point2i& point1, cv::Point2i& point2)
{
	if ((point1.x == point2.x) && (point1.y == point2.y))
	{
		return true;
	}

	return false;
}

// interpolation between not adjacent points
void get_line_points(cv::Point2i& point1, cv::Point2i& point2, std::vector& line_points)
{
	line_points.push_back(point1);

	int dx = abs(point1.x - point2.x);
	int dy = abs(point1.y - point2.y);

	if (dx == 0 && dy == 0)
	{
		return;
	}

	if (dx > dy)
	{
		if (point1.x < point2.x)
		{
			for (int i = point1.x + 1; i < point2.x; i++)
			{
				int y = (int)(((point1.y - point2.y + 0.0) / (point1.x - point2.x)) * (i - point1.x) + point1.y);
				line_points.push_back(cv::Point2i(i, y));
			}
		}
		else
		{
			for (int i = point1.x - 1; i > point2.x; i--)
			{
				int y = (int)(((point1.y - point2.y + 0.0) / (point1.x - point2.x)) * (i - point1.x) + point1.y);
				line_points.push_back(cv::Point2i(i, y));
			}
		}
	}
	else
	{
		if (point1.y < point2.y)
		{
			for (int i = point1.y + 1; i < point2.y; i++)
			{
				int x = (int)(((point1.x - point2.x + 0.0) / (point1.y - point2.y)) * (i - point1.y) + point1.x);
				line_points.push_back(cv::Point2i(x, i));
			}
		}
		else
		{
			for (int i = point1.y - 1; i > point2.y; i--)
			{
				int x = (int)(((point1.x - point2.x + 0.0) / (point1.y - point2.y)) * (i - point1.y) + point1.x);
				line_points.push_back(cv::Point2i(x, i));
			}
		}

	}

	line_points.push_back(point2);

	return;
}


bool get_spline(cv::Point2d& point1, cv::Point2d& point2, cv::Point2d& c01,
	cv::Point2d& c12, std::vector& spline_points, double delta_s)
{
	cv::Point2i point_prev = (cv::Point2i)point1;
	cv::Point2i point_last = (cv::Point2i)point2;

	spline_points.push_back(point_prev);

	for (double s = 0.0; s < (1.0 + 0.0001); s += delta_s)
	{
		double J0 = pow(1 - s, 3);
		double J1 = pow(1 - s, 2) * s * 3;
		double J2 = pow(s, 2) * (1 - s) * 3;
		double J3 = pow(s, 3);

		double ptx = point1.x * J0 + c01.x * J1 + c12.x * J2 + point2.x * J3;
		double pty = point1.y * J0 + c01.y * J1 + c12.y * J2 + point2.y * J3;

		cv::Point2i ipoint;

		ipoint.x = (int)round(ptx);
		ipoint.y = (int)round(pty);

		if (is_same_point(ipoint, point_last))
		{
			get_line_points(point_prev, point_last, spline_points);
			break;
		}

		if (is_adjcent_point(point_prev, ipoint))
		{

			spline_points.push_back(ipoint);
			point_prev = ipoint;
		}
		else if (is_same_point(point_prev, ipoint))
		{
			continue;
		}
		else
		{
			get_line_points(point_prev, ipoint, spline_points);
			point_prev = ipoint;
		}
	}
	return true;
}


void smooth_curve(std::vector& curve_in, std::vector& curve_out, bool is_closed)
{
	int vec_size = curve_in.size();

	for (int i = 0; i < (vec_size - 2); i += 2)
	{
		if (i == 0 && is_closed)
		{
			if (is_adjcent_point(curve_in[vec_size - 1], curve_in[1]))
			{
				curve_out.push_back(curve_in[1]);
			}
			else
			{
				curve_out.push_back(curve_in[0]);
				curve_out.push_back(curve_in[1]);
			}
		}

		if (is_adjcent_point(curve_in[i], curve_in[i + 2]))
		{
			curve_out.push_back(curve_in[i + 2]);
		}
		else
		{
			curve_out.push_back(curve_in[i + 1]);
			curve_out.push_back(curve_in[i + 2]);
		}
	}

	return;
}


bool get_spline_curve(std::vector& key_points, std::vector& spline_curve, double t, bool is_closed)
{
	if (key_points.size() < 2)
	{
		std::cout << "Key points is less than two!!!" << std::endl;
		return false;
	}

	if (key_points.size() == 2)
	{
		cv::Point2i point1 = (cv::Point2i)key_points[0];
		cv::Point2i point2 = (cv::Point2i)key_points[1];
		get_line_points(point1, point2, spline_curve);
		return true;
	}

	std::vector vec_c01, vec_c12;
	get_control_points_array(key_points, vec_c01, vec_c12, t);

	std::vector temp_spline;

	for (int i = 0; i < key_points.size(); i++)
	{
		if (i < (key_points.size() - 1))
		{
			get_spline(key_points[i], key_points[i + 1], vec_c12[i], vec_c01[i + 1], temp_spline, DELTA_S);
			continue;
		}

		if (is_closed)
		{
			get_spline(key_points[i], key_points[0], vec_c12[i], vec_c01[0], temp_spline, DELTA_S);
		}
	}

	smooth_curve(temp_spline, spline_curve, is_closed);

	return true;
}

2017.03.09完成初稿