用牛刀杀鸡——幂级数解数列

分享一道我的高数老师布置的高数选做题，这题磨了我整整俩到三个小时左右，最后算出来之后还是相当有成就感的。

当然在一些大佬眼里可能算不了什么。。。

下面给出题目

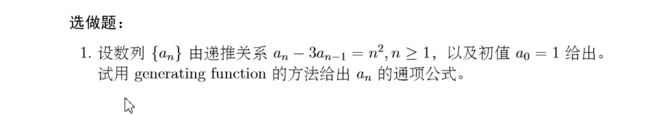本题用的知识点是幂级数的和函数那一块知识，但是解这道题目的时候远远没有这么简单。

首先面对这类题目，都是有一个固定套路，就是先想办法利用和函数把递推关系里面的数列下标统一，并且和在一起。

过程如下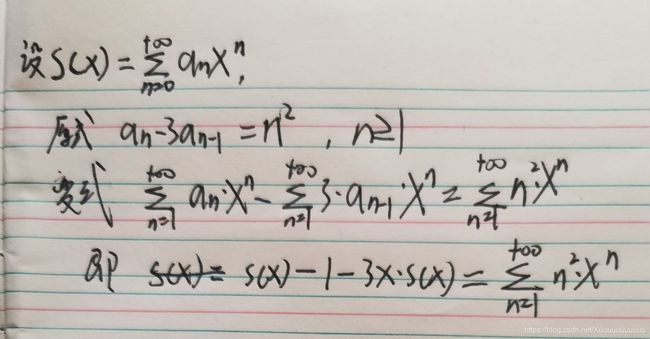
说白了就是通过一些变换，将原式变成s(x)和x的等式，然后求出和函数，再利用1/(1-x)^k 这类的幂级数公式，再将求出的和函数变成幂级数的形式，然后把x^n 前面的数拿出来，就是要求的a^n了。

思路听起来是不是很容易？其实中间还是蜿蜒曲折。。

现在我们面临的一步就是怎么求出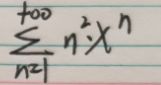
因为本人水平过低，想了很久都没想出来，最后只能求助度娘，在度娘的帮助下，我大致获得了求这个的思路。就是说，我们现在阶段要求的和函数，都必须通过求导，积分等手段往Σx^n上面去靠，这个式子求导肯定是不行的，但是通过观察，我们可以发现，通过将x提一个出来，然后对里面进行积分，就可以消去一个n，重复俩次就能变成我们想要的式子了
最后算出来这个是等于(x^ 2+x)/(1-x)^ 3 ,
代入原式，算出s(x)=1/(1-3x) + (x^ 2+x)/[(1-x)^ 3*(1-3x)],

之后就是一个比较繁琐的问题了，我们要将后面那一项拆开来，变成1/(1-x)^k 类似的分式组合。

这里我想了很久，想不出来，还是请教了一些朋友之后才解决了这个问题。
就是通过待定系数法进行拆分，具体的去网上搜部分分式展开法就能明白，由于我最近事情很多，就不在这个比较繁琐的地方浪费时间了。

下面给出展开后的结果：

可以让x等于一些简单的值来检验算出来的系数是否正确。

然后之后就比较简单了，主要就是带公式，这也是我们高数老师推出来的一个非常厉害的公式，

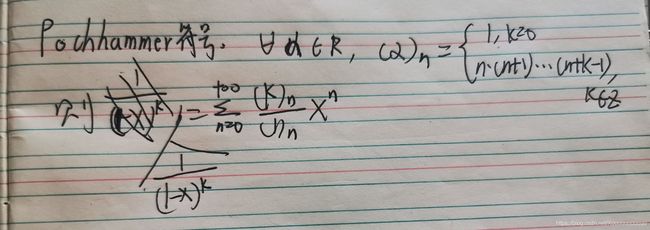
利用这个公式，再通过整合，就可以算出正确答案。（但是幂级数在最后整合这一块也是有点难度的，不信的可以去尝试一下）

最终结果如下

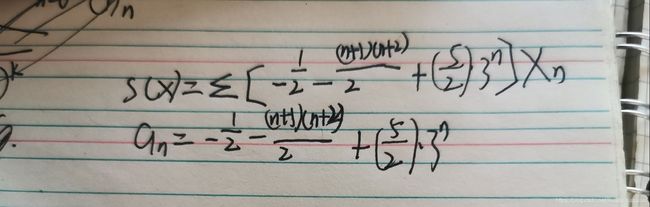
然后可以通过代入n=1,n=2进行检验（这是我高中做题时经常用的方法），就能知道自己是不是正确答案了。

体会

大学的数学不像高中，知识点好掌握，但是题目灵活多变。像大学，知识点就已经很难掌握了，那些难的题目就更不用说了。而且我们大学本科接触的数学知识（数学系以外）其实都只是冰山一角，并且大学课程讲的又很快，作为学生，你也不知道这个知识点该学到什么地步，该深入到什么地步，所以大学的数学还是相当有难度的。

但是大学的数学才真正让我领略到数学的奥妙，我真的很好奇那些惊为天人的公式到底是怎么推导出来的，数学家的脑子里到底装着什么东西？

学了一段时间再回过头来用大学的知识点去做高中的题目，确实做的很爽。

我觉得我们高数老师有句话说的很好，“当你学习学到了一种新的境界，那些所谓技巧就显得不那么重要了”

虽然我专业学的不是数学，但是我在高等数学这门课上花的时间还是比我的专业课多，我不知道这有没有意义，只能说是兴趣在后面推波助澜。

以后如果有机会，我一定会去学习数学建模，将我所学到的数学知识用于实践，服务我们的国家。毕竟12年的数学可不能白学了。。

我也深刻意识到微积分这门课对我们非数学系的学生而言其实就是一门解决实际问题的工具，我经常会一味钻到公式原理、公式推导中去，现在是知识爆炸的年代，其实很多时候我们只要会用就已经超过很多人了，毕竟我们是要去使用他们帮助我们解决问题的。我们不是天才，我们不可能做到每门课都学的很好，大学里面课程这么多，说到底还是要学会取舍，哪门课该学的深，哪门课简单掌握能用就行，这都是自己的选择，这个问题牵扯的就很复杂了，是需要结合自己兴趣，特长，专业等综合考虑的。

就一句话，“鱼和熊掌不可兼得，学会取舍，懂得加法的同时更不能忘记减法。”

如果觉得有帮助，可以关注一下我的公众号，我的公众号主要是将这些文章进行美化加工，以更加精美的方式展现出来，同时记录我大学四年的生活，谢谢你们！