分而治之（D&C）——递归思想（算法图解第一弹）

最近在看一本书叫《算法图解》，里面的内容写得都比较浅显易懂，很适合我这个菜狗学习，因此之后一段时间就通过博客记录我学习的进度。

算法的重要性就不需要我过多说了，下面我就直接开始介绍我刚掌握的一种思想，“分而治之”。

其实这个思想说白了就是如何将一个实际问题转化成递归问题。这个分而治之思想的祖宗就是递归。大一上学习这块知识的时候属实头疼了很久，这个递归算法刚开始接触的时候确实有点难度（可能也是我太菜了）

其实D&C思想就分成俩步，
一：寻找尽可能简单的基线条件。（也就是什么时候停止递归）
二：将大问题分解成一个个小问题，再将一个个小问题分解成一个个小小问题，最后让其符合基线条件，然后再慢慢回去，得出最终结果。

看着是不是挺简单的，确实，算法这东西难就难在如何将其应用到实际生活中去，而且，算法是学不完的，我们学习算法主要是要掌握其中的思想，递归算法有很多很多，但是归根结底就是“分而治之”的思想，当我们掌握了这个思想，我们在面对一系列从未接触过的实际问题的时候，才有机会去利用我们的知识去解决它。

然后算法的学习一定要有例子辅助理解，要不然啃概念会学的非常吃力（大佬忽略）。

这里我就将书本上的例子搬过来了，

第一个例子：

“假设你是农场主，有一小块土地。你如何才能将这块地均匀地分成方块，并且要保证分出的方块尽可能大？”

这个问题的关键就是要找到基线条件，也就是什么时候一块地可以均匀地分成方块，且尽可能大。通过数学知识，我们不难发现，假设土地的俩个边长是a和b,当a是a和b的最大公约数或者b是a的最大公约数时，就可以均匀分成方块，并且是最大的。

如下：

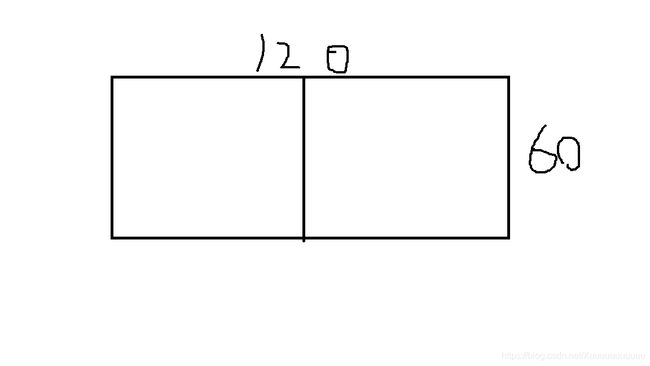
接下来我们就可以将问题进行细分，假设土地为1680×640，我们可以从这块地中划分出俩个640×640的方块，这样就剩下余下那一小块400×640的地了，然后我们就可以继续对这块余下的地重复上一步，直到最终符合基线条件。这里的难点在于，为什么前面划分出来的方块可以均匀划分成我们最终细分出来的符合基线条件的方块？真正的解释就是是伟大的欧几里得算法（想要了解的可以去网上找一下）。其实我们要求的最大划分块的边长就是a和b的最大公约数，这个如果要推导确实有点麻烦，但是我们可以在草稿纸上比划一下，其实能很轻易地理解，这个我就不放上去了。

这个是前段时间用欧几里得算法做的题
https://blog.csdn.net/Xuuuuuuuuuuu/article/details/106873282

第二个例子：

上面那个主要是通过实际问题来大致解释一下分而治之的思想，接下来就是分而治之思想在算法当中的体现。书本上选择的就是快速排序算法。

这个算法我印象中是在高中的时候有接触过，那个时候算是比较难的题目，现在经过一年大一的学习，相对来说比较轻松，但是理解归理解，难的是如何将其写成代码，应用到实践中去。

先简单介绍一下这个算法吧，从名字上看，这个算法叫“快速排序”算法，那自然是比一般的排序算法是要快的，用大O表示法就表示为O（n*logn），而常见的冒泡排序和选择排序则表示为O（n^2），这个大O表示法主要是用来表现算法的时间复杂度的，想要深入理解可以去网上搜索学习一下，这里我就不展开了。

而这个算法很大的特点就是“分而治之”，基线条件就是待排序数组中元素数目为0或者为一（记住，这里的待排序数组是动态变化的），这样就不需要排序了，然后第二步的抽象过程就是将排序问题进行分化，先从待排序数组中找到一个基准值，若是要从小到大排序，就将比这个基准值小的数放到基准值的左边，将比这个基准值大的数放到基准值的右边，之后再对基准值左边的数和右边的数继续进行分化，也就是重复上面那一步，继续排序，实现将大问题转化成小问题，再将小问题转化成小小问题的效果。

比如针对含有5个元素的待排序数组{2,1,6,3,5}，先选择基准值2，这里基准值的选择是个需要注意的点，由于我们的代码必然要写成循环的格式，因此基准值就要选择待排序数组的第一个数据或者第二个数据，这样就不会发生下标越界。

然后进行分类

之后再对左边的{1}和右边的{6,3,5}重复上一步骤即可。
这个程序如果用python的话是非常简单就能实现的，通过python强大的数组，可以说“上天入地，无所不能”。但是若是想要 用C或者C++实现就会相对麻烦一点，这里面就还会加入交换位置的知识，因为C或者C++不像python可以一步到位，它很多想要把数据挑出来放到基准值俩边其实是一个比较复杂的过程。这篇博客在这方面已经讲得很清楚了，感兴趣的可以看看这篇。

https://blog.csdn.net/weixin_42109012/article/details/91645051

第三个例子：

四天前C语言上机考的一道题目，这道题目确实有点难，我当初也是碰巧想到了思路才AC的，那些大佬们直接就A过去了，这我真的是比不上，还是自己太菜了。压轴题我连连题目都看不懂。

Problem D: KI的斐波那契

Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 869 Solved: 310

Description

KI十分喜欢美丽而优雅的斐波那契数列,最近他新认识了一种斐波那契字符串,定义如下

f (0) = b, f (1) = a,

f (2) = f (1) + f (0) = ab,

f (3) = f (2) + f (1) = aba,

f (4) = f (3) + f (2) = abaab,

…

KI想知道 f (n) 中的第 m 位是什么,你可以帮他解决这个问题吗?

Input

第一行有一个整数 T ,表示测试组数。

接下来的每个测试组包含两个数 n, m 。

数据范围: T≤ 1000, 0 ≤ n ≤ 90, 1 ≤ m ≤ 1e18

Output

对于每个测试组,输出’a’或者’b’

Sample Input

5
4 1
5 3
10 22
22 233
66 2333333333333

Sample Output

a
a
a
b
a

这道题目暴力解法是完全没用的，只是在浪费时间，因为数组完全存不下这么长的字符串。那么这类题目就不能用常规思路去解它，考试的时候我还找了半天规律，看有没什么a和b出现的规律，花里胡哨折腾了半天，还是没有什么卵用。那个时候我就联想到之前刷过的一道题目，就是《你的名字》，这道题目还是很有意思，感兴趣的可以看看下面的链接。
http://oj.acm.zstu.edu.cn/JudgeOnline/problem.php?cid=5867&pid=3

想要正着做这道题目真的是完全的自寻死路，但若是转化一下思路，倒着想就会非常简单。于是我当初就尝试了一下，还真给我摸到了一点头绪，其实这道题目就是要反着做，将很长很长的数字转化成基线数据。

既然f(n)=f(n-1)+f(n-2)，那么我是否可以把f(n)分成俩部分，一部分是f(n-1)，一部分是f(n-2)，然后当我要查找的位数是在f(n-1)中，就再次对f(n-1)重复上一步，查找的数在f(n-2)中也是同理。从这里就可以看出这就是“分而治之”的思想，将很复杂的问题转变成一个又一个小问题，再将小问题转变成一个又一个小小问题，最终就能倒推出结果，也是运气比较好吧，换平时以我这种小菜狗的水平，应该是做不出来的。

代码如下：

#include
using namespace std;
vector<int>v1;
long long a[91];
char f(int n,long long m)
{
     
    if(n==0)
    {
     
        return 'b';
    }
    else if(n==1)
    {
     
        return 'a';
    }
    else
    {
     
        if(m>a[n-1]) f(n-2,m%a[n-1]);
        else f(n-1,m);
    }
     
}
int main()
{
     
     
    a[0]=1;
    a[1]=1;
    for(int i=2;i<=90;i++) a[i]=a[i-1]+a[i-2];
    int t;
    while(cin>>t)
    {
     
        while(t--)
        {
     
            long long n,m;
            cin>>n>>m;
            cout<<f(n,m)<<endl;
        }
    }
}

当初做出来后，属实激动了很久。因为我一直认为我不是一个适合考试的学生。。。因为上学期太飘了，再加上这学期一些课程莫名其妙地歇菜，终究还是离我的预期差了一点点，没有能够把上学期的拉胯给遮起来，果然还是我太菜了。大学里面的大佬实在太多，作为小菜狗的我只能潜心修炼，尽量向大佬们寻求《真经》。

如果觉得有帮助，可以关注一下我的公众号，我的公众号主要是将这些文章进行美化加工，以更加精美的方式展现出来，同时记录我大学四年的生活，谢谢你们！