C++排列组合及应用
1. 基础
1.1. 加法原理
加法原理是分类计数原理,常用于排列组合中,具体是指:做一件事情,完成它有n类方式,第一类方式有M1种方法,第二类方式有M2种方法,……,第n类方式有Mn种方法,那么完成这件事情共有M1+M2+……+Mn种方法。
如:从武汉到上海有乘火车、飞机、轮船3种交通方式可供选择,而火车、飞机、轮船分别有k1,k2,k3个班次,那么从武汉到上海共有k1+k2+k3种方式可以到达。
1.2. 乘法原理
做一件事,完成它需要分成n个步骤,做第一 步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法。那么完成这件事共有N=m1×m2×m3×…×mn 种不同的方法。
如:从A城到B城中间必须经过C城,从A城到C城共有3条路线(设为a,b,c),从C城到B城共有2条路线(设为m,t),那么,从A城到B城共有3×2=6条路线。它们分别是:am,at,bm,bt,cm,ct。
乘法是加法的一个推论,乘法都可以分解为多个对应的数相加。
2. 排列
2.1. 定义
排列(Permutation 或者 Arrangement),从n个不同元素中,任取r(r≤n,r与n均为自然数,下同)个不同的元素按照一定的顺序排成一列,叫做从n个不同元素中取出r个元素的一个排列;从n个不同元素中取出r(r≤n)个元素的所有排列的个数,叫做从n个不同元素中取出r个元素的排列数,用符号 P(n,r)或A(n,r)表示。
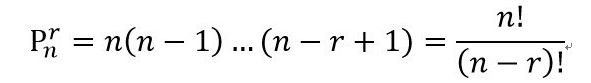
如:有10个参赛选手,最终选出1、2、3名,分析总共可能出现多少种排名情况。第1名有10种情况,第2则有9种情况,第3名则有8种情况。应用乘法原理,总共的情况即为1098,这也正好即是P(10,3)。
2.2. 全排列
当P(n,r)中的r=n时,所有的排列情况称为全排列。
STL算法中有next_permutation可以求全排列序列。也可以通过递归交换法计算一排列。
void FullPermute(int _nArr[], int _nStart, int _nCnt, vector<vector<int>>& _vvPerm)
{
if (_nStart == _nCnt)
{
vector<int> vInt(_nArr, _nArr+_nStart+1);
_vvPerm.push_back(vInt);
}
for (int nIdx = _nStart; nIdx <= _nCnt; nIdx++)
{
std::swap(_nArr[_nStart], _nArr[nIdx]);
FullPermute(_nArr, _nStart + 1, _nCnt, _vvPerm);
std::swap(_nArr[_nStart], _nArr[nIdx]);
}
}
2.3. 排列
当P(n,r)中的r
int SumPermutation(int n, int r)
{
if (r == 1)
return n;
return SumPermutation(n - 1, r - 1) * n;
}
利用全排列,从中获取相应的即可。
std::vector<std::vector<int>> Permute(int n, int r)
{
if (r > n)
{
return std::vector<std::vector<int>>();
}
std::vector<std::vector<int>> vvPerm;
std::vector<int> vInt;
for (int nIdx = 0; nIdx < n; nIdx++)
{
vInt.push_back(nIdx);
}
vvPerm.push_back(std::vector<int>(vInt.begin(), vInt.begin()+r));
int nDivisor = 1;
for (int nIdx = 1; nIdx <= (n-r); nIdx++)
{
nDivisor *= nIdx;
}
int nTotalCnt = 1;
while (std::next_permutation(vInt.begin(), vInt.end()))
{
if (0 == nTotalCnt++ % nDivisor)
{
vvPerm.push_back(std::vector<int>(vInt.begin(), vInt.begin()+r));
}
}
return vvPerm;
}
3. 组合
3.1. 定义
从n个不同元素中,任取r(r≤n)个元素并成一组,叫做从n个不同元素中取出r个元素的一个组合;从n个不同元素中取出r(r≤n)个元素的所有组合的个数,叫做从n个不同元素中取出r个元素的组合数。用符号 C(n,r) 表示。
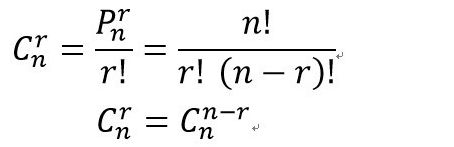
排列是与次序相关的,而组合是与次序无关的。如:有10个参赛选手(A、B、C、D、E、F、G、H、I、J),选取3名发奖牌(奖牌相同),分析总共有多少种情况。因为排列有先后,所以A、B、C和A、C、B是不同的排列情况,但是这两种在组合中被认为是相同。也就是说将排列中因为排序不同,但是实际选手组合相同的情况去除,即是组合的情况。因为排序导致的不同是C(3,3)。那么C(n,r)=P(n,r)/P(r,r)=P(n,r)/r!。
3.2. 代码
利用递归求所有组合的总数。
int SumConbinaton(int n, int r)
{
if ((r == 0) || (n == r))
return 1;
return SumConbinaton(n - 1, r - 1) + SumConbinaton(n - 1, r);
}
所有的递归都可以通过模拟栈来转为非递归。但是递归代码的可读性比循环好很多。一般情况下对速度没有特别的要求,尽量用递归算法实现。
void _Combine(int nArr[], int n, int r, int nCnt, std::vector<std::vector<int>>& vvComb)
{
if (r <= 0)
{
vector<int> vInt;
for (int nIdx = 1; nIdx <= nCnt; nIdx++)
{
vInt.push_back(nArr[nIdx] - 1);
}
vvComb.push_back(vInt);
return;
}
for (int nIdx = n; nIdx >= r; nIdx--)
{
nArr[r] = nIdx;
_Combine(nArr, nIdx-1, r-1, nCnt, vvComb);
}
}
std::vector<std::vector<int>> Combine(int n, int r)
{
std::vector<std::vector<int>> vvComb;
std::vector<int> vInt;
for (int nIdx = 0; nIdx < n; nIdx++)
{
vInt.push_back(nIdx);
}
_Combine(&vInt[0], n, r, r, vvComb);
return vvComb;
}
上面的递归代码感觉也不是特别容易理解,可以参考下面这个。
void _Combine(U8 _uCnt, U8 _uStart, U8 _uSelCnt, vector<vector<U8>>& _vvDst)
{
if (1 == _uSelCnt)
{
for (U8 idx = _uStart; idx < _uCnt; ++idx)
{
vector<U8> vTemp;
vTemp.push_back(idx);
_vvDst.push_back(vTemp);
}
return;
}
for (U8 idx = _uStart; idx < _uCnt; ++idx)
{
vector<vector<U8>> vvDst;
_Combine(_uCnt, idx+1, _uSelCnt-1, vvDst);
for (auto itDst = vvDst.begin(); itDst != vvDst.end(); ++itDst)
{
vector<U8> vDst;
vDst.push_back(idx);
vDst.insert(vDst.end(), itDst->begin(), itDst->end());
_vvDst.push_back(vDst);
}
}
}
4. 应用
4.1. 应用1
有M个球,每个球有N种颜色,那么一共有多少种情况呢?第1个球有N种可能,第2个球有N种可能…第M个球有N种可能,那么总共是M^N。
void _BuildAllState(UINT _uCnt, UINT _uValue, UINT _uIdx, vector<int> _vComb, vector<vector<int>> &_vvComb)
{
vector<int> vComb = _vComb;
for (UINT i = 0; i < _uValue; i++)
{
vComb[_uIdx] = i;
if (_uIdx+1 < _uCnt)
{
_BuildAllState(_uCnt, _uValue, _uIdx+1, vComb, _vvComb);
}
else
{
_vvComb.push_back(vComb);
}
}
}
vector<vector<int>> BuildAllState(int m, int n)
{
vector<vector<int>> vvComb;
vector<int> vInt(m , 0);
_BuildAllState(m, n, 0, vInt, vvComb);
return vvComb;
}
4.2. 应用2
有M个球,每个取N个,有多少种取法。这是典型的组合问题,即C(M,N)。
4.3. 应用3
有M个球,随意取N(N<=M)个球,继续取L(L<=M-N),直到取完所有球,分析总共有多少种情况。
void _MixConbine(int _nCnt, int _nStart, vector<vector<vector<int>>>& _vvvDst)
{
if (_nStart == _nCnt)
{
return;
}
for (int nIdx = _nStart; nIdx < _nCnt; nIdx++)
{
vector<vector<int>> vvDst;
vector<int> vDst;
for (int n = _nStart; n <= nIdx; n++)
{
vDst.push_back(n);
}
vector<vector<vector<int>>> vvvDst;
_MixConbine(_nCnt, nIdx+1, vvvDst);
if (vvvDst.size() > 0)
{
for (auto it = vvvDst.begin(); it != vvvDst.end(); ++it)
{
vector<vector<int>> vvTemp;
vvTemp.push_back(vDst);
vvTemp.insert(vvTemp.end(), it->begin(), it->end());
_vvvDst.push_back(vvTemp);
}
}
else
{
vector<vector<int>> vvTemp;
vvTemp.push_back(vDst);
_vvvDst.push_back(vvTemp);
}
}
}
vector<vector<vector<int>>> MixConbine(int _nCnt)
{
vector<vector<vector<int>>> vvvConb;
_MixConbine(_nCnt, 0, vvvConb);
return vvvConb;
}