数据结构与算法一:算法的引入与复杂度分析
Talk is cheap, show me the code.
数据结构与算法是基本功!!!
程序=数据结构+算法
一. 算法的概念及特征
算法是一种解决问题的方法和思想。算法的五大特征:
- 输入
- 输出
- 有穷性
- 确定性
- 可行性
二. 算法的效率衡量
- 时间复杂度:就是指执行一个算法的基本步骤,用大O记法衡量。
最坏时间复杂度:提供一种保证,表明算法在此种程度的基本操作中一定能完成。
一般说一个算法的时间复杂度都是指最坏情况下的时间复杂度。
最优时间复杂度:意义不大,因为指的是最优情况下的时间复杂度,只是特殊的某个情况
平均时间复杂度:
- 空间复杂度
三. 时间复杂度的几条基本计算规则
- 基本操作,即只有常数项,认为其时间复杂度为O(1)
- 顺序结构,时间复杂度按加法进行计算
- 循环结构,时间复杂度按乘法进行计算
- 分支结构,时间复杂度取最大值
- 判断一个算法的效率时,往往只需要关注操作数量的最高次项,其它次要项和常数项可以忽略
- 在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度
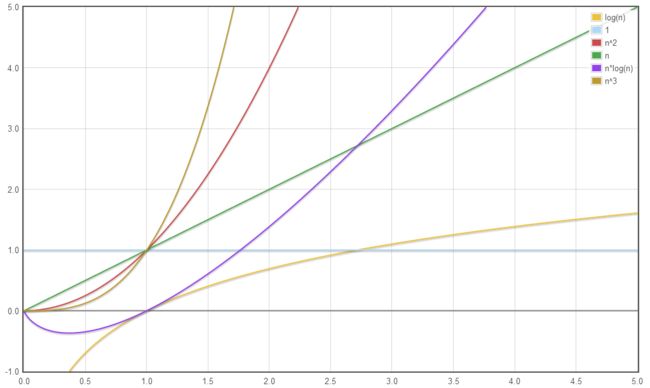
时间复杂度比较:
O(1) 图片来源:https://my.oschina.net/pokdars/blog/819327 数据结构大致分成:线性结构和非线性结构 线性结构包括线性表,字符串,栈,队列等 使用线性表存储数据的方式可以这样理解,即“把所有数据用一根线儿串起来,再存储到物理空间中”.。 线性表用于存储逻辑关系为“一对一”的数据。 线性表包括顺序表和链表。 将数据依次存储在连续的整块物理空间中的存储结构; 顺序表的操作: a. 在尾端加入元素:时间复杂度为O(1) b. 非保序的加入元素(不常见):时间复杂度为O(1) c. 保序的元素加入:时间复杂度为O(n) a. 删除表尾元素,时间复杂度为O(1) b. 非保序的元素删除(不常见),时间复杂度为O(1) c. 保序的元素删除,时间复杂度为O(n) Python中的list和tuple两种类型采用了顺序表的实现技术,具有前面讨论的顺序表的所有性质。 tuple是不可变类型,即不变的顺序表,因此不支持改变其内部状态的任何操作,而其他方面,则与list的性质类似。 Python标准类型list就是一种元素个数可变的线性表,可以加入和删除元素,并在各种操作中维持已有元素的顺序(即保序),而且还具有以下行为特征: 在Python的官方实现中,list就是一种采用分离式技术实现的动态顺序表。这就是为什么用list.append(x) (或 list.insert(len(list), x),即尾部插入)比在指定位置插入元素效率高的原因。 在Python的官方实现中,list实现采用了如下的策略:在建立空表(或者很小的表)时,系统分配一块能容纳8个元素的存储区;在执行插入操作(insert或append)时,如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大(目前的阀值为50000),则改变策略,采用加一倍的方法。引入这种改变策略的方式,是为了避免出现过多空闲的存储位置。 数据分散的存储在物理空间中,通过一根线保存着它们之间的逻辑关系的存储结构。每个数据元素在存储时都配备一个指针,用于指向自己的直接后继元素。 在每一个节点(数据存储单元)里存放下一个节点的位置信息(即地址)。 同顺序表和链表一样,栈也是用来存储逻辑关系为 "一对一" 数据的线性存储结构。 栈(stack),有些地方称为堆栈,是一种容器,可存入数据元素、访问元素、删除元素,它的特点在于只能允许在容器的一端(称为栈顶端指标,英语:top)进行加入数据(英语:push)和输出数据(英语:pop)的运算。没有了位置概念,保证任何时候可以访问、删除的元素都是此前最后存入的那个元素,确定了一种默认的访问顺序。 由于栈数据结构只允许在一端进行操作,因而按照后进先出(LIFO, Last In First Out)的原理运作。 图片来源:https://blog.51cto.com/9291927/2063393?source=drt 栈具有先进后出的特性,适用于检测就近匹配的成对出现的符号。 队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。 队列是一种先进先出的(First In First Out)的线性表,简称FIFO。允许插入的一端为队尾,允许删除的一端为队头。队列不允许在中间部位进行操作!假设队列是q=(a1,a2,……,an),那么a1就是队头元素,而an是队尾元素。这样我们就可以删除时,总是从a1开始,而插入时,总是在队列最后。这也比较符合我们通常生活中的习惯,排在第一个的优先出列,最后来的当然排在队伍最后。 图片来源:http://data.biancheng.net/view/10.html 包括普通树,二叉树,线索二叉树等; 图片来源:https://www.cnblogs.com/QG-whz/p/5168620.html 多对多的关系 图片来源:https://segmentfault.com/a/1190000010794621 参考资料: 黑马程序员/传智播客
python list 内置操作的时间复杂度
操作
时间复杂度
index
O(1)
append
O(1)
pop
O(1)
pop(i)
O(n)
insert(i,item)
O(n)
reverse()
O(n)
sort()
O(nlogn)
slice [x:y]
切片, 获取x, y为O(1), 获取x,y 中间的值为O(k)
python dict 内置操作的时间复杂度
操作
时间复杂度
get (key)
O(1)
delete (key)
O(1)
copy
O(n)
四. 数据结构
I. 线性结构
1. 线性表(全名为线性存储结构)
1.1. 顺序存储结构(简称顺序表):
1.2. 链式存储结构(简称链表):
2. 栈
栈的应用
符号匹配问题
从第一个字符开始扫描,遇到普通字符时忽略,遇到左符号时压入栈,遇到右符号时弹出栈顶元素进行匹配。如果匹配成功,所有字符扫描完毕并且栈为空;如果匹配失败,所有字符扫描完成但栈非空。3. 队列
II. 非线性结构:
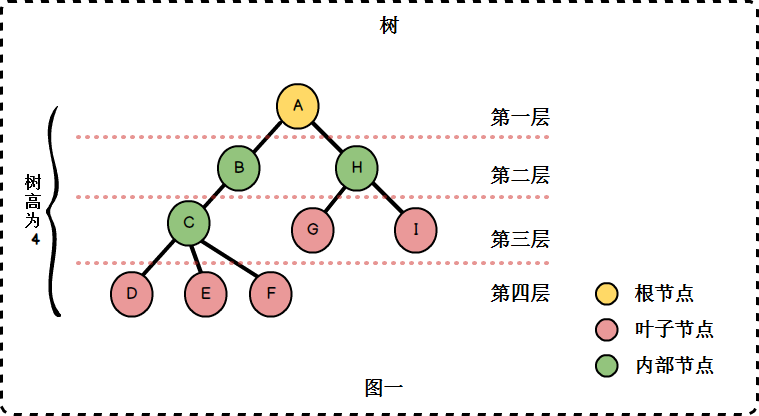
1. 树
2. 图Graph