团灭Leetcode打家劫舍问题

开篇

动态规划的问题我们已经说过很多了，今天这篇博客将是最后一篇面试题详解中的动态规划算法问题，接下来我们会对其他算法进行一些类型题的更新——如回溯法，贪心法。以及一些数据结构的典型例题，如hash，链表，栈，二叉搜索树(这个是最重要的)，堆(优先队列)等等进行基础问题的更新。(主要借鉴labuladong的文章及顺序)
今天我们要说的以是一道leetcode上的一种类型题——打家劫舍。我在大二的时候，基本毫无算法基础，仅仅会python和C++编程，就受到了某些名人的怂恿，大胆地去面试了，现在想想当初自己真的自信，反而现在有了算法功底以后开始惧怕笔试题了，可能这就是传说中的无知者无畏吧哈哈哈哈。当初面试的时候面试官让我手撕代码，就是打家劫舍问题，当时根本没有leetcode的概念，计算机基本0基础，想靠着自己仅有的C++的基本语句蒙混过关，然而结局可以预知的惨烈，但是打家劫舍问题其实就是一种很简单的动态规划问题，代码量少，思路简单，这篇文章就带你团灭掉所有打家劫舍类型题。

打家劫舍问题

打家劫舍问题一


我们发现我们不能偷相邻的两个住户，因此如果你偷了1号，2号就不能再偷了，但是你可以偷三号…找出最大的偷窃金额即可。
典型的动态规划问题，我们还是按照老方法——找状态，穷举，做选择
我们先考虑一下状态是什么，状态就是住户的序号和现有金额，而抢或者不抢就是我们的选择。

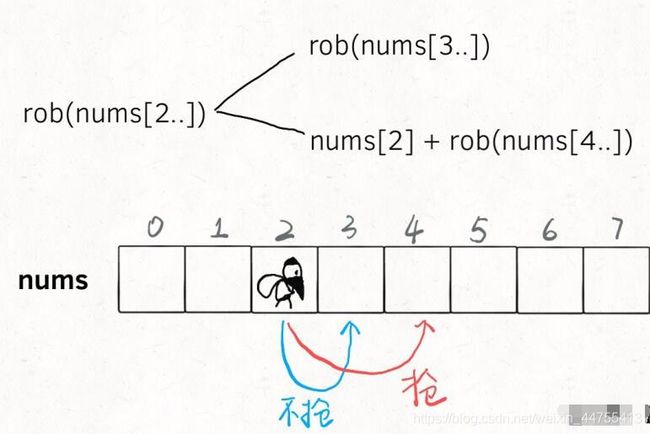
在两个选择种，每次都选更大的结果，最后得到的就是最多能抢到的钱：

int rob(int nums[])
{
     
	return dp(nums,0);
}
//返回nums[start....]能抢到的最大值
int dp(int nums[],int start)
{
     
	if(start >= nums.length())
		return 0;
	int res = max(
	//不抢，去下家
	dp(nums,start+1),
	//抢，去下下家
	dp(nums[start]+dp[nums,start+2]);
	)
	return res;
}

从代码中我们其实就已经明确了状态转移，就可以发现对于同一个start位置，是存在重叠子问题的，比如下图:

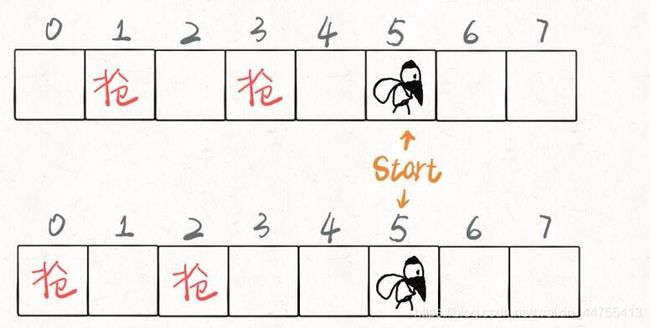
上述代码我们每次都会进入一个递归之中，但是这样岂不是很浪费时间？所以说存在重叠子问题，可以用备忘录进行优化，在上述的代码中进行优化，在每次求解之前现在备忘录中查找，如果查找得到就直接返回，否则就计算结果:max(nums[start] + dp(nums,start+2),dp(nums,start+1))
上述都是一些自顶向下的方法，但我们也可以采用自底向上的方法，从n-1遍历到0.
我们又发现，状态转移之和dp[i]最近的两个状态有关，所以可以进一步优化，将空间复杂度降低为O(1)

int rob(int nums[])
{
     
	int n = nums.length();
	//记录dp[i+1]和dp[i+2]
	int dp_i_1 = 0,dp_i_2 = 0;
	//记录dp[i]
	int dp_i = 0;
	for(int i = n - 1;i >= 0;i--)
	{
     
		dp_i = max(dp_i_2 + nums[i],dp_i_1);
		dp_i_2 = dp_i_1;
		dp_i_1 = dp_i;
	}
	return dp_i;
}	

打家劫舍问题二
这个问题基本和问题一是一样的，只不过房子的排列方式略有不同，问题一里房子排列成了一排，而问题二中所有房子围成了一个圈。所以第一家住户和最后一家住户不能同时被偷。
这里的解决办法其实没什么特别的，和问题一有异曲同工的技巧。只不过在这里，我们限定选择住户的范围。
我们知道，动态规划法最重要的就是状态和选择。问题一里我们直接在所有房子中考虑我们偷哪些房子。但是在问题二中，我们需要限定一下考虑的范围，不能在所有房子中进行考虑，而只能在部分房子中考虑。
由于，首尾两个住户不能投同时被偷，我们就限定两个范围，第一个范围包括首，不包括尾；第二个范围包括尾不包括首。但其实还有一种范围，就是二者都不包括，但是这种范围一定比前两者偷到的钱数少，所以我们不做考虑。

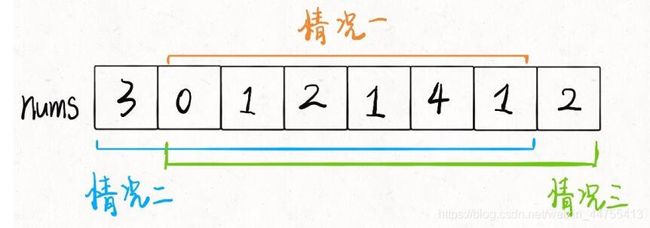
int rob(int nums[])
{
     
	int n = sizeof(nums) / sizeof(nums[0]);
	if(n==1)return nums[0];
	return max(robrange(nums,0,n-2),robrange(nums,1,n-1));
}
//仅计算闭区间[start,end]的最优结果
int robrange(int nums[],int start,int end)
{
     
	int n = sizeof(nums) / sizeof(nums[0]);
	int dp_i_1 = 0,dp_i_2 = 0;
	int dp_i = 0;
	for(int i = end;i >= start;i--)
	{
     
		dp_i = max(dp_i_1,nums[i]+dp_i_2);
		dp_i_2 = dp_i_1;
		dp_i_1 = dp_i;
	}
	return dp_i;

打家劫舍问题三
问题三也是改变了所有住户的住房结构，不再是一排或者一圈了，而是一棵二叉树。房子在二叉树的节点上，相连的两个房子不能同时被抢劫。

我们的整体思路没有变，仍然是在枪和不抢中去做选择，我们可以直接套用代码

int rob(TreeNode root)
{
     
	int res[] = dp(root);
	return max(res[0],res[1]);
}

//返回一个大小为2的数组arr
//arr[0]表示不抢root的话可以得到的最大钱数
//arr[1]表示抢root的话可以得到的最大钱数
vector<int>dp(TreeNode root)
{
     
	if(!root)
		return [0,0];
	//其中left[0]表示左边不抢，left[1]表示左边抢，right同理
	vector<int>left = dp(root.left);
	vector<int>right = dp(root.right);
	//抢，下家就不能抢了
	int rob = root.val+left[0]+right[0];
	//不抢，下家可以抢也可以不抢，取决于收益
	int not_rob = max(left[0],left[1])+max(right[0],right[1]);
	return [rob,not_rob];	

时间复杂度为O(N)，空间复杂度只有递归函数堆栈所需的空间，不需要备忘录的额外空间
大家也可以选择备忘录的方式，这里说一下大致的思路和关键的状态转移方程，不写代码了：
首先创建一个hashtable来存储访问每个结点对应的最大钱数，这样下来可以节省一些时间，状态转移方程也是采用递归的方式：

int rob(TreeNode root)
	//抢根节点
	int do_it = root.val + 
	(root.left == null ? 0 : rob(root.left.left) + rob(root.left.right)) +
	(root.right==null ? 0 : rob(root.right.right)+rob(root.right.left));
	//不抢根节点
	int not_do_it = rob(root.left) + rob(root.right);
	int ans = max(do_it,not_do_it);
}		

总结

这是动态规划的最后一篇文章了，在这里最后对动态规划做一下总结。
动态规划其实最重要的框架再说下去就吐了，状态，选择，状态转移方程
如果我们能写出状态转移方程和base case，那么问题基本就解决了90%了，但是状态转移方程起码要有状态吧，所以确定状态也是很重要的。所以大家在读题的时候一定要找出题目中的所有状态(与答案密切相关的可变量)，然后对状态穷举，专注于写出状态转移方程，然后写出base case，基本就八九不离十了。
有的朋友一定会说，这个状态转移方程那哪有那么容易写啊。是的，我到现在都有这样的感觉，但是当你刷题多了，会发现状态转移方程就那么几种，见得多了自然能想到了。在这一系列面试题详解的动态规划和我的另一系列动态规划专栏的文章中，基本介绍了所有动态规划的典型问题，状态转移方程无非这几种，大家可以多看多思考，学会状态转移方程的书写，基本可以秒杀动态规划问题。