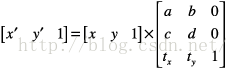Quartz 2D 小结

graphics context 

在ios的Quartz中。所有的绘图都有一个上下文环境。定义着绘图所需要的各种参数信息以及绘制需要的设备信息。在这里需要你创建使用的。一般情况也就 bitmap images和 pdf context。

在我们ios里面需要自己来绘制的时候。一般情况下都是重写 uiview 的 draw:rect 方法。在这个方法里面。 系统已经为我们准备好了上下文对象并且以及放到了栈顶。我们可以调用 UIGraphicsGetCurrentContext 方法来获取到当前的context 对象。

Coordinator Systems

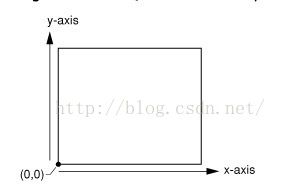
在Quartz坐标系中。原点是在左下角。向上，向右 是增加（图1）。跟uikit是不同的。在uikit的坐标系中。左上角是原点。向下 向右增加在这里需要注意。当我们使用 UIGraphicsGetCurrentContext的时候。这个context是经过转换的。即 左上角才是原点.这里需要了解一下 current transformation matrix。

 图1  Quartz 坐标系

current transformation matrix

可以称为 CTM。 用来转换设备空间 和用户空间。 在ios中，Quartz 2D 绘制模块定义了2种坐标空间（coordinate space）。用户空间（user space）和设备空间（device space）。 用户空间可以理解为我们操作的文档页面。而设备空间是真正的设备物理分辨率。他们之间就是通过CTM进行转换的。通过这个我们能够实现 页面的 移动，缩放，旋转，剪切等。

你可以直接改变CTM来达到移动 缩放 旋转 剪切的功能。通过类似下面的方法：

CGContextTranslateCTM  //移动
CGContextRotateCTM  //旋转
CGContextScaleCTM  //缩放
CGContextClipToMask // 遮罩/剪切  根据遮罩的图片的 透明度 决定剪切.  可以参考这个文章 ：http://blog.sina.com.cn/s/blog_78a55c9f0101037i.html

affine transform  

这个是一个 3X3 的矩阵。CTM 就是根据这个值对坐标系进行转换的。你可以通过CGContextGetCTM 方法获取到当前的值。我在5 和 6P 的iphone的uiview 的draw 方法里面调
用这个函数打印出来的值分别是：

(a = 2, b = 0, c = 0, d = -2, tx = 0, ty = 1136)

(a = 3, b = 0, c = 0, d = -3, tx = 0, ty = 1704)

这样可以看到 6P 的缩放比 是3. 5上面是2 。并且 在这里 跟原始坐标系对比 已经进行过翻转了。

你也可以创建一个 affine transform 对象。然后设置给需要改变的对象 来改变 ctm。他的基本构造方法（其实反而不常用的方法）是 

 CGAffineTransformMake(CGFloat a, CGFloat b, CGFloat c, CGFloat d, CGFloat tx, CGFloat ty) 这个方法是所有构造方法中 唯一一个需要了解这个 3X3 矩阵到底是怎么回事的方法。如图2 所示。构造方法里面的6个参数分别对应图中 3X3 对应位置的值。（这里需要注意 矩阵的 第三列 永远是 0，0，1 ） 图3 所示就是利用矩阵的乘法。转化 （x，y） 坐标到 （x‘，y’）坐标。 结果如图4 所示。 所以 在很多场合下面 我们都把 b 和 c 永远设置为0. 这样 a 就表示 横向的缩放比例。 d表示 纵向的缩放比例。 tx表示横向位移。ty表示 纵向位移。

图2 affine transform表示的矩阵 图3 矩阵乘法图4用户空间上的点通过矩阵转化成设备空间上的点

旋转就稍微复杂一点：

一个点P（x，y）旋转到 P'（x‘，y’）那么 根据三角函数的 和与差：

cos(α+β)=cosα·cosβ-sinα·sinβ

sin(α+β)=sinα·cosβ+cosα·sinβ

α,β 是 P和P‘连线远点 跟 x轴的夹角

 β= α +a（旋转的角度）；

以单位圆考虑 那么

x= cosα  * 1；

y=sinaα  * 1；

x’= cosβ  * 1；

y‘=sinaβ  * 1；

所以 

x‘ = cos β  = cos（α+ a）=cosα·cosa-sinα·sina=x*cosa - y*sina；

y’=sinβ  = sina（α+ a）=sinα·cosa+cosα·sina=y*cosa + x*sina；

我们在看看旋转的 affine transform 的矩阵应该怎么赋值 图5所示

图5 旋转矩阵的赋值

旋转前的点（x，y，1）跟这个矩阵相乘可以得到

x‘ = x*cosa + y*（-sina）

y’=x*sina + y*cosa 跟上面一致。

当然大多数情况 我们不需要使用CGAffineTransformMake 这个来自己构建这个 affine transform。毕竟还是有点小复杂的。系统提供了一系列的方法可以直接获取到一些常用的affine transform。

CGAffineTransformMakeTranslation

CGAffineTransformTranslate

CGAffineTransformMakeRotation

CGAffineTransformRotate

CGAffineTransformMakeScale

CGAffineTransformScale

每2个时一对。一个是从原始矩阵得到的。另外一个是根据你穿进去的参数得到新的矩阵。看方法名也能知道 分别是 移动 旋转 和缩放

这里有一个很特别的方法

CGAffineTransformInvert

反转矩阵。非常有用。当你改变一个坐标系进行一系列操作之后想恢复的时候。通过你改变的矩阵的 反转矩阵在改变一下。就可以恢复到原始状态了。

改变当前的affine transform 通过方法：CGContextConcatCTM(CGContextRef c, CGAffineTransform transform) 来实现。

另外还可以不改变整个context 的affine transform 有这样几个方法

CGPointApplyAffineTransform 只改变这个点

CGSizeApplyAffineTransform//改变size

CGRectApplyAffineTransform//改变rect

另外还有2个比较有用的东西

CGAffineTransformIdentity 于是矩阵 。就是 原始矩阵 a=1 b=0 c=0 1d= tx=0 ty=0

CGAffineTransformIsIdentity 判断是不是原始矩阵。

绘图函数

在上面可以了解到 绘图的信息都是保存在上下文 context 对象中。 其中 affine transform 负责对坐标系进行转换。接下来记录一下我们常用的绘图函数。

一般情况我们绘制有2种需求。一时绘制各种形状。对这些形状进行填充 剪切等各种操作然后就出现了我们需要的绘制的内容。

另外一种是绘制图片，文字等。如果是第一种情况。我们必须先了解一个对象：CGPathRef 。这个定义了你要绘制的路径。需要注意这个并不绘制形状。只是定义了绘制的路径。接下来了解一下跟 CGPathRef 相关的函数：

首先必须要了解2个最重要的方法：

CGContextBeginPath //开始新的路径 之前的路径被抛弃！！！！

CGContextMoveToPoint //从给定的点 开始新的subPath 加入到 主 path 内去.所以操作的环境也会切换到新创建的subpath 当中去.

无论如何他们都牵扯到一个东西 path。path 是有一系列的形状 或者 supath 组成。 而我们画图基本上就是在操作path。最后调用 StrokePath方法对 线条填充。 或者 fill 方法对封闭的形状进行填充。

对path 的操作方法主要有：

CGContextAddLineToPoint

CGContextAddRect

CGContextAddArc

CGContextAddArcToPoint

CGContextAddCurveToPoint

看方法名称也能知道是干什么。对于下面的 二次贝塞尔曲线 以及三次贝塞尔曲线。 牵扯到数学了本人也不是很了解。

上面的那些方法都是对当前上下文操作的对象进行处理。比如 CGContextAddArc 就是在当前的path 上面绘制圆弧。我们也可以自己创建 path 对象然后在自己创建的path上面进行操作。这样就可以把这个path缓存下来。重复利用。

通过CGPathCreateMutable 创建自己的 path。对path 的操作 跟上面的方法很像 就是将 CGContext 前缀 换成了 CGPath 前缀。

大体就这些。具体的操作查看api 就行了。

其他

这里我会不断更新 工作中遇到或者有新的理解的东西：

1.关于view太大 内存问题：

最近我遇到一个问题。有个一自定义 绘图的view。我是放到scrollView上面根据数据多少决定view大小。然后可以滚动。 当数据非常大的时候。（我的那个 view的宽度为 30000）导致内存暴涨500M。只要重写 draw:rect 方法就会这样。即使这个方法里面一行代码页没有。最后猜测 当你重写了draw 方法的时候 。系统会为你准备绘图环境。这里消耗 的内存 增长非常大。 所以也可以变相知道 draw:rect 方法是个非常耗性能的方法。

2.CGContextSaveGState 和 CGContextRestoreGState

这2个方法我忽略的比较的多。以前没有用到。直到一次看别人的代码才发现。是个好东西.作用是 复制一个当前context。并且将它压入栈顶。另外一个方法当然就是出栈了。通过这2个方法。我们可以很容易实现 改变上下文然后恢复到之前上下文的功能。

3.关于清除view的绘图

以前我一直以为draw：rect 每一次执行都会清空之前的。重新绘制。直到一次才发现并没有。后台才明白 设置背景色 才是导致每次看到的draw：rect 都好像是重新绘制的原因。