简单易懂堆排序
# 什么是堆?
1.堆是一个完全二叉树
2.任意非叶子节点的值大于等于(大顶堆)或小于等于(小顶堆)其左右孩子的值.
这就说明根元素的值是堆中最大或最小的.
如果我们输出堆顶元素, 然后对剩下的元素重新调整为一个堆, 如此直到输出所有元素, 便可完成排序了.
但是有个问题, 初始给定的数据不是一个堆啊, 所以我们要先将其初始化为堆.
因此, 实现堆排序需要解决两个问题: 1. 将一个无序序列构建为一个堆 2.输出堆顶元素后, 调整堆.
# 通常的结构
物理结构为一个数组, 逻辑结构为完全二叉树.
用 n 表示最大下标则:
array[0] 为堆顶
array[i] 的左孩子为 array[2*i+1], 右孩子为 array[2*i+2] i >= 0 && i <= (n-1)/2
# 堆排序过程
1. 怎么构建一个堆呢?
也就是说我们要将一个最大/最小的元素放到堆顶
那就在堆顶 array[0], 左子树 array[1], 右子树 array[2] 中"选择"一个最大的放到 array[0]
那左子树 array[1] 的最大元素呢? 我想聪明的你应该想到了, 继续同样的操作就行了.
这里的"选择"就是一个调整堆的过程. 所以现在我们将问题转化为调整堆了.
2. 调整堆
我们给定序列 8, 9, 6, 7, 9, 7
创建的大顶堆如下, 这时 array[0] 即为此序列的最大元素
输出堆顶元素(和序列最后一个元素交换位置)
这时就破坏了大顶堆, 我们先调整(6, 9, 7), 选择一个最大的与根交换
由于交换又破坏了左子树, 那就继续调整, 直到所以遭破坏的树调整完毕即可
有可能破坏的树只有交换后的子树.
输出堆顶元素(交换), 此时堆顶元素为序列中次大的元素
同样调整堆
继续输出
调整
交换输出
调整
交换输出, 只剩下一个元素, 此时排序完成
如此, 我们可以看出大顶堆完成是从小到大的排序
稍微想一下, 小顶堆则完成的是从大到小的排序
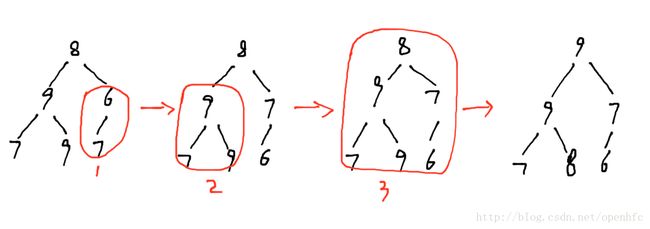
此时我们再看创建大顶堆的过程, 就比较清楚了. 依次队非叶子节点调整
# 代码
static void adjust_heap(int *keys, int first, int last) {
int root, child;
// child 开始为左孩子
for (root = first; (child = root * 2 + 1) <= last; root = child) {
// 在左右孩子中选择一个最大的, 此时最大的元素下标为 child
if (child + 1 < last && keys[child+1] > keys[child]) {
child = child + 1;
}
// 如果孩子中最大的比父节点大, 则与父节点交换, 并以此孩子节点为根继续调整 root = child
if (keys[child] > keys[root]) {
swap(&keys[child], &keys[root]);
// 如果在没交换的情况下, 父节点就是最大的, 则无需再继续调整
} else {
break;
}
}
}
void heap_sort(int *keys, int len) {
int i;
// 使len为最大索引
len -= 1;
// 构造大顶堆, 此时保证 keys[0] 为最大元素
for (i = (len-1)/ 2; i >= 0; --i)
adjust_heap(keys, i, len);
for (i = len; i > 0; ) {
// 将 keys[0] 放到尾部,
swap(&keys[i], &keys[0]);
// 移除最大元素, 调整堆
adjust_heap(keys, 0, --i);
}
}