力扣面试题62. 圆圈中最后剩下的数字

0,1,,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

 

示例 1：

输入: n = 5, m = 3
输出: 3

示例 2：

输入: n = 10, m = 17
输出: 2

 

限制：

    1 <= n <= 10^5
    1 <= m <= 10^6

 

约塞夫问题：

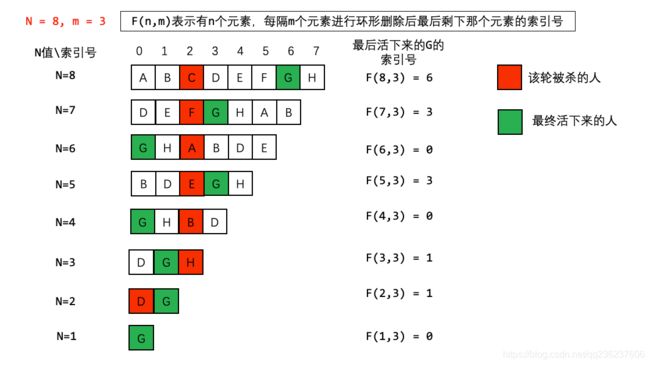
下面这个例子是N=8 m=3的例子

我们定义F(n,m)表示最后剩下那个人的索引号，因此我们只关系最后剩下来这个人的索引号的变化情况即可

从8个人开始，每次杀掉一个人，去掉被杀的人，然后把杀掉那个人之后的第一个人作为开头重新编号

    第一次C被杀掉，人数变成7，D作为开头，（最终活下来的G的编号从6变成3）
    第二次F被杀掉，人数变成6，G作为开头，（最终活下来的G的编号从3变成0）
    第三次A被杀掉，人数变成5，B作为开头，（最终活下来的G的编号从0变成3）
    以此类推，当只剩一个人时，他的编号必定为0！（重点！）

3 最终活着的人编号的反推

现在我们知道了G的索引号的变化过程，那么我们反推一下
从N = 7 到N = 8 的过程

如何才能将N = 7 的排列变回到N = 8 呢？

我们先把被杀掉的C补充回来，然后右移m个人，发现溢出了，再把溢出的补充在最前面

神奇了 经过这个操作就恢复了N = 8 的排列了！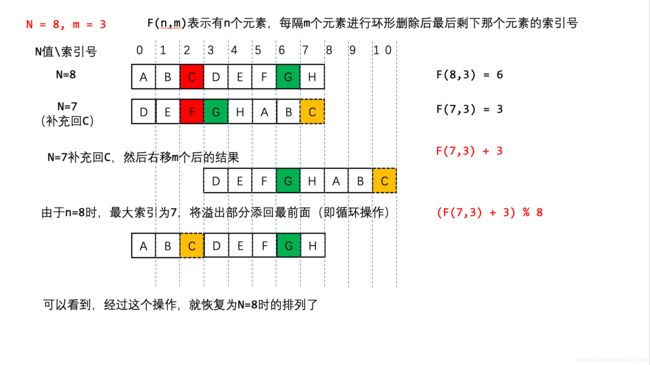

因此我们可以推出递推公式f(8,3)=[f(7,3)+3]%8
进行推广泛化，即f(n,m)=[f(n−1,m)+m]%n
4 递推公式的导出

再把n=1这个最初的情况加上，就得到递推公式

f(n,m)=0，n=1

f(n,m)=[f(n−1,m)+m]%n，n>1

 

class Solution(object):
    def lastRemaining(self, n, m):
        """
        :type n: int
        :type m: int
        :rtype: int
        """
        p = 0
        for i in range(2, n + 1):
            p = (p + m) % i
        return p